1 Kompleksiluvut

1.1 Määritelmä

Tarkastellaan euklidista tasoa

R² = {(x,y) | x,y Î R}.

Kuva 1: Euklidinen taso R²

Suorakulmaisessa koordinaatistossa on x-akseli ja y-akseli. Luvut x ja y ovat pisteen z = (x,y) koordinaatteja. Tavalliseen tapaan x-akseli voidaan tulkita reaalilukujen joukoksi R. Täll"in x-akselia kutsutaan reaaliakseliksi ja sitä voidaan tarvittaessa merkitä symbolilla R. Pistettä z = (x,0) kutsutaan reaaliluvuksi. Täll"in voidaan merkitä z = x Î R.

Algebrallisesti R on kunta. Reaaliluvuilla on määritelty yhteenlasku ja kertolasku siten, että tavalliset laskukaavat ovat voimassa. Erityisen mielenkiintoisia ovat tulon merkkis„„nn”t:

kertojan merkki	kerrottavan merkki	tulon merkki
+	+	+
+	-	-
-	+	-
-	-	+

Hämmästyttävää on, että my"s negatiivisen luvun neli" on positiivinen. Eräs selitys l"ydetään laajentamalla R:n laskutoimitukset koko tasoon.

Reaalilukujen yhteenlaskun laajentaminen reaaliakselilta koko tasoon on helppoa. Jos

z₁ = (x₁,y₁) ja z₂ = (x₂,y₂)

ovat kaksi pistettä, niin summaksi

z₁+z₂ = (x₁+x₂,y₁+y₂)

kelpaa tavallinen "vektorisumma".

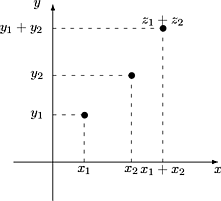
Kuva 2: Kompleksilukujen summa

Jos y₁ = y₂ = 0 eli pisteet ovat reaaliakselilla (ts. ovat reaalilukuja), niin z₁+z₂ on tavallinen reaalilukujen summa. (Merkitään z = x, kun z = (x,0).)

Kertolaskun laajentaminen ei ole yhtä helppoa, sillä valmiina ei ole sopivaa "vektorituloa". Kertolaskun laajentamista varten esitetään tason pisteet z = (x,y) ¹ (0,0) napakoordinaattien r ja j avulla:

ì
í
î

x = r cosj

y = r sinj

Kuva 3: Kompleksilukujen napakoordinaattiesitys

Merkitään z = (r,j). Tulo on nyt määriteltävissä yksinkertaisella kaavalla

z₁z₂ = (r₁r₂,j₁ + j₂).

Siis: Pisteiden z₁ ja z₂ etäisyydet origosta kerrotaan keskenään sekä vaihekulmat lasketaan yhteen.

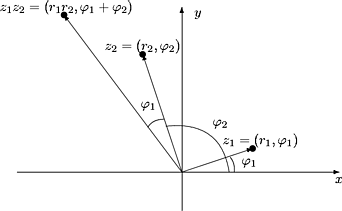
Kuva 4: Kompleksilukujen tulo

Erikoisesti on z₁z₂ = 0 aina ja vain kun z₁ = 0 tai z₂ = 0.

Tarkastellaan reaalilukujen kertolaskua tämän uuden kertolaskun valossa. Olkoon z = (r,j) reaaliluku.

Kuva 5: Puhtaasti reaaliset kompleksiluvut

Täll"in aina |z| = r. Lisäksi

z = r > 0

j = 0 + n2p

z = -r < 0

j = p+ n2p

Jos nyt z₁ = (r₁,j₁) ja z₂ = (r₂,j₂) ovat kaksi reaalilukua, niin z₁z₂ = (r₁r₂,j₁+j₂), joten

z₁z₂ > 0

j₁+j₂ = 0+n2p

j₁ = j₂ = 0+n2p tai j₁ = j₂ = p+n2p

z₁ > 0 ja z₂ > 0 tai z₁ < 0 ja z₂ < 0.

Reaalilukujen tulon merkkisäänn"t ja uuden kertolaskun määritelmä liittyvät toisiinsa kauniilla tavalla.

1.2 Kertolasku suorakulmaisissa koordinaateissa

Muodostetaan kertolaskun lauseke xy-koordinaateissa. Olkoot

z₁ = (x₁,y₁), z₂ = (x₂,y₂).

Silloin

x₁ = r₁cosj₁,

y₁ = r₁sinj₁

x₂ = r₂cosj₂,

y₂ = r₂sinj₂

Jos merkitään

z₁z₂ = (x,y) = (r cosj, r sinj),

niin r = r₁r₂ ja j = j₁ + j₂.

Siis

r₁r₂cos(j₁+j₂)

r₁r₂cosj₁cosj₂-r₁r₂sinj₁sinj₂

(r₁cosj₁)(r₂cosj₂)-(r₁sinj₁)(r₂sinj₂)

x₁x₂-y₁y₂,

r₁r₂sin(j₁+j₂)

r₁r₂sinj₁ cosj₂ + r₁r₂cosj₁ sinj₂

(r₁cosj₁)(r₂ sinj₂)+(r₂ cosj₂)(r₁ sinj₁)

x₁y₂+x₂y₁.

Algebrasta tuttu kaava

z₁z₂ = (x₁y₁)(x₂,y₂) = (x₁x₂-y₁y₂,x₁y₂+x₂y₁)

seuraa siis kertolaskun (geometrisesta) määritelmästä. Algebrassa on tästä kaavasta lähtemällä voitu helposti todistaa, että (R²,+,·) on kunta. Sille käytetään merkintää C ja sen alkioita kutsutaan kompleksiluvuiksi.

Yhtäl"llä

z² = -1

ei ole tulon merkkisäänt"jen nojalla ratkaisua reaalilukujen kunnassa R. Tutkitaan, onko sillä ratkaisua kompleksilukujen kunnassa C. Koska 0² = 0, riittää tarkastella kompleksilukuja z ¹ 0. Olkoon z:lla napakoordinaattiesitys

z = (r,j).

Silloin z² = (r²,2j) ja -1 = (1,p), joten

z² = -1

ì
í
î

r² = 1

2j = p+n2p

ì
í
î

r = 1

j = p/2 + np

Kuva 6: Yhtäl"n z² = -1 ratkaisut

Yhtäl"llä z² = -1 on siis kaksi ratkaisua

ì
í
î

z₁ = (0,1) (n = 0,2,4,...)

z₂ = (0,-1) (n = 1,3,5,...),

missä z₂ = -z₁.

Merkitään i = (0,1). Silloin i² = -1. Lukua i kutsutaan imaginaariyksik"ksi, ja y-akselia imaginaariakseliksi. Muotoa z = (0,y) = iy olevia kompleksilukuja kutsutaan puhtaasti imaginaarisiksi. Muistamme, että muotoa z = (x,0) = x olevia kompleksilukuja kutsutaan reaalisiksi. Jos

z = (x,y) = x(1,0)+y(0,1) = x ·1+yi = x+iy,

niin

x = Re z

on z:n reaaliosa ja

y = Im z

on z:n imaginaariosa. Molemmat ovat siis reaalisia, joten

z = Re z + i Im z .

Lukua

= (x,-y) = x-iy

kutsutaan z:n liittoluvuksi eli kompleksikonjugaatiksi. Määritelmistä seuraa, että

(z₁+z₂)

z₁

z₂

z₁z₂

z₁

z₂

(

)

z +

2 Re z

z -

2i Im z.

Jos z = (r, j), niin [`(z)] = (r,- j). Kuvaus z ® [`(z)] on peilaus x-akselissa.

Oliko edellä tehty merkintä z = x+iy täysin perusteltu? Olkoon z = (x,y) kompleksiluku ja t = (t,0) reaalinen kompleksiluku. Silloin

tz = (t,0)(x,y) = (tx-0y,ty+0x) = (tx,ty).

Jos t ¹ 0, on

Kompleksiluku kerrotaan (ja jaetaan) reaaliluvulla siis samalla tavalla kuin lineaarialgebrassa vektori kerrotaan (ja jaetaan) reaaliluvulla.

Lineaarialgebran tapaan R²:ssa käytetään nyt kantaa e₁ = 1 = (1,0), e₂ = i = (0,1) ja laskut todellakin on luvallista suorittaa "tavallisten" algebran kaavojen mukaisesti:

z = (x,y) = (x,0)+(0,y) = x(1,0)+y(0,1) = x ·1 + y ·i = x+iy.

Tavallinen algebra sujuu näillä lausekkeilla samoilla säänn"illä kuin reaalilukujen algebra. Ainoa ero on, että

i²

-1

i³

-i

i⁴

i⁵

i⁶

-1

i⁷

-i

i⁸

1 jne.

(Lisäksi on i⁰ = 1 ja i¹ = i).

Kompleksiluvun z = x+iy itseisarvolla eli modulilla |z| tarkoitetaan vektorin (x,y) pituutta

|z| =

_____
Öx²+y²

Jos t > 0, niin |tz| = t|z|.

Lause 1 |z| = Ö{z [`(z)]} ( = |[`(z)]|).

Todistus. Ö{z [`(z)]} = Ö[((x+iy)(x-iy))] = Ö[(x²-(iy)²)] = Ö[(x²+y²)] = |z|.

Kompleksiluvun z ¹ 0 vaihekulmaa j kutsutaan sen argumentiksi argz. Näin ollen

arg

- argz

|z| cos(argz)

|z| sin(argz)

|z| (cos(argz) + i sin(argz))

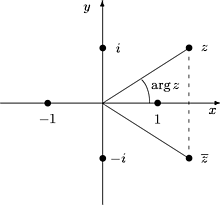
Kuva 7: Kompleksiluvun argumentti ja liittoluku

Usein merkitään r = |z| ja j = argz. Silloin

z = r(cosj+ i sinj).

Kertolaskun geometrisen määritelmän perusteella

|z₁z₂|

|z₁||z₂|

arg(z₁z₂)

argz₁+ argz₂.

Täydellisen induktion periaatteesta seuraa, että

|z₁z₂ ¼z_n|

|z₁||z₂| ¼|z_n|

arg(z₁z₂ ¼z_n)

argz₁ + argz₂ + ¼+ argz_n

z₁z₂ ¼z_n

r₁r₂ ¼r_n(cos(j₁+j₂ ¼+ j_n)+i sin(j₁ + j₂ + ¼+ j_n)).

1.3 Käänteisluku ja jakolasku.

Olkoon z ¹ 0. Silloin

|z|²

x²+y²

-i

x²+y²

z₁

z₂

z₁

|z₂|²

x₁x₂+y₁y₂-i(x₁y₂-x₂y₁)

x₂²+y₂²

z₂

z₁ = z₁

z₂

Jakolaskussa lukujen hajottaminen reaali- ja imaginaariosiin pidentää lausekkeita huomattavasti.
Kaavoista seuraa

ê
ê
ê

|z|²

ê
ê
ê

|z|²

ê
ê
ê

|z|²

| =

|z|

|z|²

|z|

ê
ê
ê

z₁

z₂

ê
ê
ê

|z₁|

|z₂|

arg

æ
ç
è

|z|²

ö
÷
ø

= arg

|z|²

+ arg

= 0- argz = - argz

arg

z₁

z₂

arg

æ
ç
è

z₁

z₂

ö
÷
ø

= argz₁+ arg

z₂

Kahden kompleksiluvun z₁ ¹ 0 ja z₂ ¹ 0 osamäärä muodostetaan jakamalla itseisarvot keskenään ja vähentämällä nimittäjän argumentti osoittajan argumentista. Kyseessä on siis my"s geometrisesti kertolaskulle käänteinen laskutoimitus.

1.4 Esimerkkejä.

1. Suorita jakolasku [(1+i)/(2-i)], ts. jaa [(1+i)/(2-i)] reaali- ja imaginaariosiin.

Tehtävä ratkaistaan poistamalla i nimittäjästä. Jos lavennetaan nimittäjän liittoluvulla, nimittäjään tulee |2-i|², joka on reaalinen:

1+i

2-i

(1+i)(2+i)

(2-i)(2+i)

(1+i)(2+i)

2²-(i)²

2+3i-1

1+3i

2. Vastaavasti
a) ¹/_i = [(-i)/(i(-i))] = -i
Re ¹/_i = 0, Im ¹/_i = -1
b) [(3+2i)/(1-i)] = [((3+2i)(1+i))/((1-i)(1+i))] = [(3-2+5i)/2] = ¹/₂ + i ⁵/₂

3. Olkoon z ¹ i . Laske | [(z-i)/(1+iz)] |.
Ratkaisu:

ê
ê
ê

z-i

1+iz

ê
ê
ê

z-i

1+iz

æ
ç
è

z-i

1+iz

ö
÷
ø

z-i

1+iz

1-i

|z|²+1+i(z-

)

1+|z|²+i(z-

)

= 1

Toinen tapa:

z-i

1+iz

z-i

i(-i+z)

= -i

4. Olkoon z₁ = x₁ +iy₁ ja z₂ = x₂ + iy₂. Silloin

z₁

x₁ -iy₁

z₂

x₂-iy₂ .

Siis

z₁+z₂

z₁

z₂

Koska

z₁z₂ = x₁x₂-y₁y₂+i(x₁y₂+x₂y₁),

z₁z₂

z₁

z₂

Koska

z₁

z₂

x₁x₂+y₁y₂-i(x₁y₂-x₂y₁)

x₁²+y₂²

æ
ç
è

z₁

z₂

ö
÷
ø

z₁

z₂

5. Kolmioepäyhtäl" Olkoot a ja b kompleksilukuja. Silloin

|a+b |²

(a+b)(

) = |a|²+|b|²+ a

|a|²+|b|²+ a

)

|a|²+|b|² + 2 Re a

Vastaavasti

|a-b |

(a-b)(

) = |a|²+|b|²-a

|a|²+|b|²- 2 Re a

Laskemalla yhteen saadaan hupaisa kaava

| a+b | + | a-b | = 2( |a| + |b|)

eli suunnikkaan lävistäjien neli"iden summa on kaksi kertaa sivujen neli"iden summa.
Koska

|a| =

(Re a)² + (Im a)²

- |a| £ Re a £ |a|,- |a| £ Im a £ |a|.

Koska kertolaskun geometrisen määritelmän mukaan | a[`(b)] | = |ab|, on

-|ab| £ Re a

£ |ab|,

joten

| a+b |²

|a|² + |b|² + 2|a||b| = (|a|+|b|)²

| a+b |²

|a|²+|b|²-2|a||b| = (|a|-|b|)².

Tuloksena on tavallinen kolmioepäyhtäl":

| |a|-|b| | £ | a+b | £ |a|+|b|,

joka nyt on voimassa my"s kompleksiluvuille. Soveltamalla kolmioepäyhtäl"ä esitykseen z = x+iy saadaan

| |x|-|y| | £ |z| £ |x|+|y|.

1.5 Moivre'n kaava.

Olkoon z = r(cosj+ i sinj). Silloin

zⁿ = rⁿ(cosnj + i sinnj).

Jos valitaan r = 1, jolloin z = cosj+isinj, saadaan ns. Moivre'n kaava

(cosj+i sinj)² = cosnj +i sinnj.

Tämä on kätevä moninkertaisten kulmien sinien ja kosinien laskemiseen. Valitaan esim. n = 5.

                               1
                             1   1
                           1   2   1
                        1    3   3   1
                      1    4   6   4   1
                    1   5   10   10  5   1

Kuva 8: Pascalin kolmio

(cosj+isinj)⁵ = cos⁵j+5icos⁴jsinj-10cos³jsin²j-10icos²jsin³j+5cosjsin⁴j+isin⁵j.

Näin ollen

cos5j

Re (cosj+isinj)⁵

cos⁵j-10cos³jsin²j+5cosjsin⁴j

sin5j

Im (cosj+isinj)⁵

sin⁵j-10cos²jsin³j+5cos⁴jsinj.

Näitä voidaan vielä muokata eri muotoihin.Sijoitetaan esimerkiksi ensimmäiseen sin²j = 1-cos²j :

cos5j

cos⁵j-10cos³j(1-cos²j+5cosj(1-cos²j)²

cos⁵j-10cos³j+10cos⁵j+5cosj(1-2cos²j+cos⁴j)

16 cos⁵j-20cos³j+5cosj.

Vastaavasti

cos3j

Re (cosj+isinj)³

Re (cos³j+3icos²jsinj-3cosjsin²j-isin³j)

cos³j-3cosjsin²j

cos³j-3cosj(1-cos²j)

4cos³j-3cosj.

Tästä seura esimerkiksi kaava

cos³j =

cos3j+

cosj.

Unohtuneet kaavat on helppo johtaa:
Koska

cos2j+isin2j

(cosj+isinj)²

cos²j+2isinjcosj-cos²j

cos2j

cos²j-sin²j,

sin2j

2sinjcosj.

1.6 Eulerin kaava.

Jos x Î R, niin

e^x

1+x+

x²

x³

x⁴

+ ¼

cosx

x²

x⁴

x⁶

+ ¼

sinx

x³

x⁵

x⁷

+ ¼.

Toisaalta

i¹

i²

-1

i³

-i

i⁴

i⁵

i⁶

-1

i⁷

-i jne.

Sijoitetaan e^x:n sarjakehitelmään x = ij. Silloin

e^ij

1+ij-

j²

-i

j³

j⁴

j⁵

j⁶

-i

j⁷

+ ¼

cosj+isinj,

joten olemme saaneet ns. Eulerin kaavan

e^ij = cosj+isinj.

Tämän perusteella kompleksiluvuilla z, argz = j, |z| = r, on esitys

z = re^ij.

Moivren kaava saa muodon

(e^ij)ⁿ = e^inj.

1.7 Esimerkkejä.

1. Laske (1+iÖ3)⁶ Moivren kaavan avulla.

Kuva 9:

(1+iÖ3)⁶ = 2⁶e^{i[(6 p)/3]} = 2⁶e^2pi = 64.

2. Ratkaise yhtäl" z³ = 1.
Merkitään z = re^ij. Silloin z³ = r³e^3ij. Koska |e^3ij | = 1, on

|z|³

r³ | e^3ij | = r³ = 1 Û r = 1.

z³ = 1

r = 1 ja e^3ij = 1 = e^n2pi, n = 0,±1,±2,... .

z³ = 1

j = n

p, n = 0,±1,±2,... .

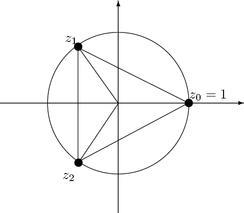
Kuva 10: Yhtäl"n z³ = 1 ratkaisut

z₁ = cos120^°+isin120^° = -

Ö3

z₂ =

z₁

= -

-i

Ö3

Tarkastus:

Ö3

)³

+3i

Ö3

+ 3

-i(

Ö3

)³

= 1.

Yleisesti ottaen binomiyhtäl"n

zⁿ = 1

juuret ovat yksikk"ympyrän kehällä. Ne sijaitsevat säänn"llisen n-kulmion kärjissä, jonka yksi kärki on pisteessä 1.

3. Ratkaise yhtäl" z⁴ = 1.
Piirretään yksikk"ympyrä ja sen sisään neli", jonka yksi kärki on pisteessä z = 1.

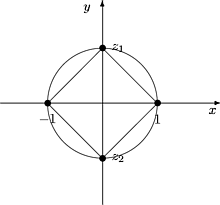
Kuva 11: Yhtäl"n z⁴ = 1 ratkaisut

Juuret ovat neli"n kärjissä:

z₁

z₂

z₃

-1

z₄

-i.

4. Laske e^ip.

e^ip = cosp+isinp = -1.

1.8 Binomiyhtäl"

Yleisellä binomiyhtäl"llä tarkoitetaan yhtäl"ä

zⁿ = w,

missä z on tuntematon ja w annettu kompleksiluku. Edellä käsiteltiin muotoa

zⁿ = 1

(1)

olevia erikoistapauksia. Jos merkitään z = re^ij, saadaan (1) muotoon

rⁿ e^{i nj} = 1 Û

ì
í
î

= 1

= k2p.

Yhtäl"n (1) juuret ovat siis

z_k:

ì
ï
ï
í
ï
ï
î

= 1

= k

, k = 0,±1,±2,¼.

Kun k = 0, saadaan triviaali juuri z₀ = 1.
Kun k = 1, saadaan niin sanottu n:s yksikk"juuri

z₁ = e^i[(2p)/(n)] = cos

+isin

jolle käytetään merkintää e_n. Koska

e_n^k = e^ik[(2p)/(n)] = z_k,

voidaan muut (1):n juuret esittää e_n:n potensseina, ja kaikki e_n:n potenssit ovat (1):n juuria.

Yhtäl"llä (1) on täsmälleen niin monta juurta kuin e_n:llä on eri potenssia. Nämä ovat

e_n⁰

e_n¹

e_n

e_n²

e_n^n-1

sillä

e_nⁿ

e^{i n[(2p)/(n)]} = e^2pi = 1

e_nⁿ⁺¹

e_n

e_nⁿ⁺²

e_n² jne.

(Kun lasketaan pelkästään luvuilla e_n^k, joiden moduli =1, on kertolasku pelkkää argumenttien yhteenlaskua.)
Binomiyhtäl"llä (1) on täsmälleen n kpl eri juurta. Nämä sijaitsevat kompleksitasossa sen säänn"llisen n-kulmion kärjissä, jonka yksi kärki on pisteessä z = 1 ja keskipiste on origossa.

Kuva 12: Yhtäl"n z⁸ = 1 ratkaisut

Esimerkki. Olkoon a yhtäl"n

1+z+z²+z³+z⁴ = 0

(2)

juuri. Osoita, että my"s a² on yhtäl"n juuri.
Ratkaisu: Koska

1-z⁵ = (1-z)(1+z+z²+z³+z⁴)

ja z = 1 ei ole (11):n juuri, on

1+z+z²+z³+z⁴ = 0 Û z⁵ = 1, z ¹ 1.

Näin ollen a = e₅^k jollakin k = 1,2,3,4.

Kuva 13:

Täll"in a² ¹ 1. Toisaalta a² = e₅^2k on yhtäl"n z⁵ = 1 juuri. Siis a² on (11):n juuri.

Sama tehtävä ei onnistu, jos astelukua nostetaan yhdellä:

(1+z+z²+z³+z⁴+z⁵)(1-z) = 1-z⁶.

a = -1 on yhtäl"n 1+z+z²+z³+z⁴+z⁵ = 0 juuri, mutta a² = 1 ei ole.

Kuva 14:

Siirrymme nyt yleiseen binomiyhtäl""n

zⁿ = w = re^iy, y > 0.

(3)

Sijoituksella z = re^ij saadaan

rⁿe^{i nj} = re^iy Û

ì
í
î

rⁿ

= r

= y+k2p, k = 0,±1,±2,....

Yhtäl"llä (3) on juuret

z_k:

ì
ï
ï
ï
í
ï
ï
ï
î

n æ
Ö

, k = 0,±1,±2,... .

Merkitään

z₀ =

n æ
Ö

e^i[(y)/(n)].

Silloin muut juuret ovat

z₁

z₀e_n

z₂

z₀ e_n²

z_n-1

z₀ e_n^n-1

Juuret z₀,...,z_n-1 sijaitsevat sen säänn"llisen n-kulmion kärjissä, jonka yksi kärki on pisteessä z₀ ja keskipiste on origossa.

Kuva 15:

Esimerkki. Yhtäl"n z⁴ = -1 = e^ip juuret ovat

z₀ = e^i[(p)/4] =

Ö2

Kuva 16:

z₁

Ö2

z₂

Ö2

-i

Ö2

z₃

Ö2

-i

Ö2

eli z₂ = -z₀, z₃ = [`(z₀)], ja z₁ = -[`(z₀)].