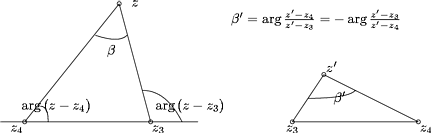2  Kompleksitason geometriaa ja topologiaa

Tavallisessa analyyttisessä geometriassa käyrien yhtäl"t esitetään x-koordinaattien ja y-koordinaattien avulla, esimerkiksi

y = 1
x
esittää tasasivuista hyperbeliä, jonka asymptootteina ovat koordinaattiakselit. Jos käyrän yhtäl""n sijoitetaan
x = 1
2
 (z+
z
 
 ),        y = 1
2i
 (z-
z
 
 ),
saadaan yhtäl" kompleksimuotoon, ts. muotoon
F(z,
z
 
 ) = 0.
Esimerkki.
y
= 1
x
Ž
1
2i
 (z-
z
 
 ) = 1
1
2
 (z+
z
 
 )
Ž
1
4i
 (z-
z
 
 )(z+
z
 
 ) = 1
Ž
z2-
z
 
 2
 
 +z
z
 
 -z
z
 
 -4i = 0
Ž
z2-
z
 
 2
 
 -4i = 0.
Kokeilu:
z
=
(1,1) = 1+i
z
 
=
1-i
z2-
z
 
 2
 
 -4i
=
1-1+2i-(1-1-2i)-4i = 0.
Analyyttinen geometria kompleksilukumerkinn"in näyttäisi olevan hyvin kätevä ratkaisu.

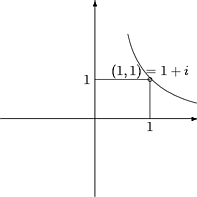
Kuva 17: Tasasivuinen hyperbeli

Jos kääntäen on annettu muotoa F(z,[`(z)]) = 0 oleva yhtäl", niin se hajoaa kahdeksi yhtäl"ksi:

F(z,
z
 
 ) = 0 Ū ģ
ļ
ļ
ķ
ļ
ļ
ī
Re F(z,
z
 
 ) = 0
Im F(z,
z
 
 ) = 0
Kun näihin vielä sijoitetan z = x+iy ja [`(z)] = x-iy, saadaan kaksi reaalista kahden tuntemattoman yhtäl"ä. Jotta yhtäl" F(z,[`(z)]) = 0 esittäisi tasokäyrää, on yleensä näiden kahden yhtäl"n oltava oleellisesti samoja eli esitettävä samaa käyrää (tai toisen yhtäl"n oltava identtisesti voimassa).

Esimerkki.
Hajotetaan z2-[`(z)]2-4i = 0 reaali- ja imaginaariosiin.

Re (z2-
z
 
 2
 
 -4i)
=
Re (z2-
z
 
 2
 
 = Re [(z-
z
 
 )(z+
z
 
 )]
=
Re (2iy2x) = 0        kaikille (x,y)
Im (z2-
z
 
 2
 
 -4i)
=
Im (z2-
z
 
 2
 
 )-4i = Im (4ixy)-4i = 4ixy-4i = 0
Ū
xy = 1 Ū y = 1
x
 .

2.1  Suoran yhtäl".

Tavallisessa muodosso suoran yhtäl" on
Ax+By+C = 0;  A,B,C Ī R,  A2+B2 > 0.
Sijoitetaan x = 1/2(z+[`(z)]),  y = [1/(2i)](z-[`(z)]):
A
2
 (z+
z
 
 )+ B
2i
 (z-
z
 
 )+C = 0
,
A(z+
z
 
 )-iB(z-
z
 
 )+2C = 0
,
(A-iB)z+(A+iB)
z
 
 +2C = 0.
Merkitään A+iB = a ja 2C = b. Silloin yhtäl" tulee muotoon
a
 
 z+a
z
 
 +b = 0;  a ¹ 0,  b Ī R
(4)
Suoran yhtäl" on siis aina tyyppiä (4).

Tarkastellaan kääntäen yhtäl"ä

az+ b
z
 
 + g = 0
ja oletetaan, että a = [`(b)] ¹ 0 ja g Ī R. Silloin
0
=
az+ b
z
 
 + g =
b
 
 z+ b
z
 
 + g
=
2 Re 
b
 
 z+ g.
Olkoon b = A+iB ja 1/2g = C. Silloin yhtäl" tulee muotoon
0
=
Re 
b
 
 z+ 1
2
 g = Re ( (A-iB)(x+iy) )+C
=
Ax+By+C.
Kaikki muotoa (4) olevat yhtäl"t esittävät siis suoraa.

Mitä sitten esittää yhtäl"

az+b
z
 
 + g = 0,
(5)
jos kertoimet a,b ja g eivät toteuta ehtoja a = [`(b)] ja g Ī R? Olkoot siis a,b,g Ī C, |a|+|b| > 0. (Jos a = b = 0, yhtäl" surkastuu.) Tässä on ehkä parasta sijoittaa
a
=
a1+ia2,
b
=
b1+ib2,
g
=
c1+ic2,
z
=
x+iy,
z
 
=
x-iy.
Yhtäl" tulee muotoon
0
=
(a1+ia2)(x+iy)+(b1+ib2)(x-iy)+c1+ic2
=
a1x-a2y+b1x+b2y+c1+i(a2x+a1y+b2x-b1y+c2)
=
(a1+b1)x-(a2-b2)y+c1+i((a2+b2)x+(a1-b1)y+c2 )
Ū
ģ
ķ
ī
(a1+b1)x-(a2-b2)y+c1 = 0
(a2+b2)x+(a1-b1)y+c2 = 0
(6)
Yhtäl" hajoaa siis kahden suoran yhtäl"ksi.
1) Toinen yhtäl" toteutuu identtisesti
a) c2 = (a1-b1) = (a2+b2) = 0 eli g Ī R ja a = [`(b)]. Tämä tapaus oli edellä esillä ja se esittää yhtä suoraa.
b) c1 = (a2-b2) = a1?+b1 = 0
Esittää yhtä suoraa (alempi yhtäl"). Itse asiassa tämä tilanne palautuu edelliseen korvaamalla (5) yhtäl"llä
iaz+ib
z
 
 +ig = 0,
sillä
ig
=
-c2+ic1
ib
=
-b2+ib1
ia
=
-a2+ia1.

2) Yhtäl"t (6) esittävät kahta toisiaan leikkaavaa suoraa, jolloin (5) esittää yhtä pistettä.
3) Suorat (6) ovat yhdensuuntaisia

Ū
0
=
ź
ź
ź
a1+b1
-a2+b2
a2+b2
a1-b1
ź
ź
ź
Ū
a12+a22
=
b12+b22
Ū
|a|
=
|b|
Jos suorat (6) eivät ole samoja, (5) ei esitä mitään.
4) Suorat (6) ovat samoja.
a) c1 = c2 = 0 ja |a| = |b|
Suorat (6) kulkevat origon kautta. (5) esittää origon kautta kulkevaa suoraa aina, kun |a| = |b| ja c1 = c2 = 0.
b) c1 ¹ 0,     c2 ¹ 0 ja |a| = |b|.
Joka tapauksessa suorat ovat yhdensuuntaisia eli |a| = |b|. Olkoon
t = a1+b1
a2+b2
 = -a2+b2
a1-b1
 .
Lisäksi a2+b2 ¹ 0, a1b1 ¹ 0, koska alempi yhtäl" on mahdoton. Suorat ovat samoja Ū [(c1)/(c2)] = t.
Yhtäl" (5) näyttäisi esittävän suoraa siis tapauksissa 1)a), 1)b), 4)a) ja 4)b).

Suoran esittäminen parametrimuodossa.

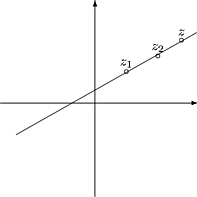
Kuva 18: Pisteiden z1, z2 ja z3 kautta kulkeva suora

Pisteiden z1 ja z2 kautta kulkevan suoran yhtäl" voidaan esittää muodossa

z = z1+t(z2-z1),     t Ī R.
Kun t = 0 saadaan z = z1 ja kun t = 1 saadaan z = z2. Kun 0 < t < 1, on z pisteiden z1 ja z2 välissä.
Eliminoidaan parametri t seuraavasti:
z-z1
=
t(z2-z1),
z
 
 -
z1
 
=
t(
z2
 
 -
z1
 
 ),
joten
z-z1
z
 
 -
z1
 
 = z2-z1
z2
 
 -
z1
 
 ,
mikä on eräs tapa muodostaa pisteiden z1 ja z2 kautta kulkevan suoran yhtäl". Tämä on yhtäpitävä muodon
arg z-z1
z
 
 -
z1
 
=
arg z2-z1
z2
 
 -
z1
 
 +n2p,
arg(z2-z1) - arg(
z
 
 -
z1
 
 )
=
arg(z2-z1)-arg(
z2
 
 -
z1
 
 )+n2p
2arg(z-z1)
=
arg(z2-z1)+n2p
kanssa. Itse asiassa tämä on geometrisesti luontevin tapa ilmoittaa pisteiden z1 ja z2 kautta kulkevan suoran yhtäl". Kompleksimerkintä antaa siis hyvin erilaisia mahdollisuuksia käsitellä analyyttistä geometriaa.

2.2  Ympyrän yhtäl".

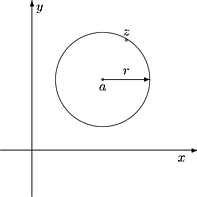
Kuva 19: a-keskinen r-säteinen ympyrä

Jos ympyrän K = K(a,r) keskipiste on a ja säde r > 0, sen yhtäl" voidaan esittää muodossa

|z-a| = r
eli
|z-a|2 = r2
eli
(z-a)(
z
 
 -
a
 
 ) = z
z
 
 -
a
 
 z-a
z
 
 +|a|2 = r2
eli
z
z
 
 +az+b
z
 
 +g = 0,
(7)
missä a = [`(b)] jag Ī R, g = |a|2-r2,  r2 = |a|2-g > 0 eli g < a[`(a)] = ab. Tämä poikkeaa suoran yhtäl"stä ainoastaan termillä z[`(z)].

Kääntäen, jos on annettu a = a-ib, b = a+ib ja g Ī R, voidaan (7) kirjoittaa muotoon

x2+y2+(a-ib)(x+iy)+(a+ib)(x-iy)+g
=
x2+y2+2(ax+by)+g = 0
Ū
(x+a)2+(y+b)2 = a2+b2-g
Tämä on ympyrä, jos r2 = a2+b2-g > 0. Keskipiste on täll"in (-a,-b).

Yhtäl" z[`(z)]+az+ b[`(z)]+g = 0 esittää ympyrää, jos ja vain jos a = [`(b)] ja g Ī R, g < ab.

2.3  Esimerkkejä.

1. Millä ehdolla kolme eri pistettä z1, z2, z3 ovat samalla suoralla? Mitä suoran esitystapaa kannattaa käyttää?

Eräs järkevä ehto saadaan lähtemällä pisteiden z1 ja z2 kautta kulkevan suoran parametriesityksestä

z = z1+t(z2-z1),     t Ī R
Piste z3 on tällä suoralla, jos ja vain jos jollekin t Ī R on voimassa
z3 = z1+t(z2-z1)
Ū
z3-z1 = t(z2-z1)
Ū
z3-z1
z2-z1
 = t.
Ehto on siis: osamäärä [(z3-z1)/(z2-z1)] on reaalinen. Toisin sanoen
arg z3-z1
z2-z1
=
np
arg(z3-z1)
=
arg(z2-z1)+np.

Esim. Ovatko pisteet 1+i, 2+3i, 3+5i samalla suoralla?

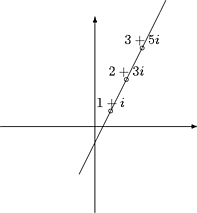
Kuva 20: Pisteet 1+i, 2+3i ja 3+5i

Ratk. z1 = 1+i, z2 = 2+3i, z3 = 3+5i.

z3-z1
z2-z1
=
3+5i-1-i
2+3i-1-i
 = 2+4i
1+2i
=
(2+4i)(1-2i)
(1+2i)(1-2i)
 = 2+8-4i+4i
5
=
2 Ī R.
Siis pisteet ovat samalla suoralla.

2. Mikä on sen ympyrän yhtäl", joka kulkee origon kautta ja jonka keskipiste on 1+i?

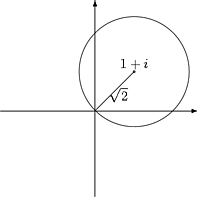
Kuva 21:

Eräs muoto:

|z-1-i| = Ö2
Tätä voidaan muokata:
2 = |z-1-i|2 = (z-1-i)(
z
 
 -1+i) = z
z
 
 +(-1+i)z+(-1-i)
z
 
 +2.
Yhtäl" tulee muotoon
z
z
 
 +(-1+i)z+(-1-i)
z
 
 = 0.
Tässä
a
=
-1+i,
b
=
-1-i,
g
=
0,
joten a = [`(b)] ja g < ab = 2.

Suora pisteiden 1+i ja -1+2i kautta.

z
=
1+i+t(-1+2i-1-i)
=
1+i+t(-2+i)
=
1-2t+i(1+t).
Eliminoidaan t:
ģ
ļ
ķ
ļ
ī
z-1-i = t(-2+i)
z
 
 -1+i = t(-2-i)
Ū z-1-i
z
 
 -1+i
=
-2+i
-2-i
(-2-i)z+2+2i+i-1
=
(-2+i)
z
 
 +2-2i-i-1
(-2-i)z+(2-i)
z
 
 +6i
=
0.
Tämä on tyyppiä 1)b). Kerrotaan yhtäl" i:llä:
(1-2i)z+(1-2i)
z
 
 -6 = 0.
Tämä on yhtäl"n perusmuoto.

4. Olkoon z suoran

(1+i)z+(1-i)
z
 
 +1 = 0
piste. Millä suoralla ovat pisteet z+i?
Merkitään w = z+i. Silloin z = w-i, joten
0
=
(1+i)(w-i)+(1-i)(
w
 
 +i)+1
=
(1+i)w+(1-i)
w
 
 +1-i+1+i+1
=
(1+i)w+(1-i)
w
 
 +3.

5. Oletetaan, että pisteet z1, z2, z3, z4 eivät ole samalla suoralla ja toteuttavat ehdon

z1-z3
z1-z4
 : z2-z3
z2-z4
 Ī R.
Osoitettava, että pisteet ovat samalla ympyrän kaarella.
Koulugeometria: Niiden pisteiden ura, josta annettu jana näkyy annetun kulman suuruisessa kulmassa, on janan päätepisteiden kautta kulkeva ympyräkaari.

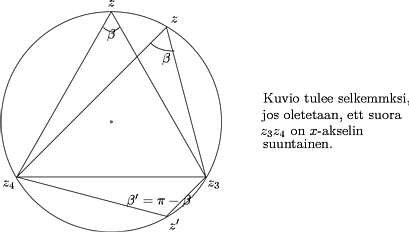
Kuva 22:

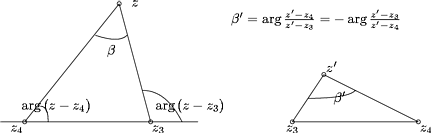
Kuva 23:

Kolmiossa kahden kulman summa=kolmannen vieruskulma. Siis b = arg(z-z3)-arg(z-z4) = arg[(z-z3)/(z-z4)].

z1-z3
z1-z4
 : z2-z3
z2-z4
 Ī R
Ū
arg é
ź
ė 		z1-z3
z1-z4
 : z2-z3
z2-z4
 ł
ś
ū 		= np,  n = 0,±1,±2,¼
Ū
arg z1-z3
z1-z4
 = arg z2-z3
z2-z4
 +np
Ū
z1 ja z2   ympyrällä, josta jana z3z4 näkyy vakiokulmassa.

2.4  Kompleksitason metriikka.

Olkoon d:C×C® R kuvaus, jolle

d(z1,z2) = |z1-z2|.
Täll"in d on metriikka C:ssä, sillä
1.
d(z1,z2) ³ 0 "z1,z2 Ī C
2.
d(z1,z2) = 0 Ū z1 = z2
3.
d(z1,z2) = d(z2,z1) "z1,z2 Ī C
4.
d(z1,z3) = |z1-z3| = |z1-z2+z2-z3|
£ |z1-z2|+|z2-z3| = d(z1,z2)+d(z2,z3) "z1,z2,z3 Ī C.

Esimerkkejä.
1. Määrää lausekkeen |z2+2iz| suurin ja pienin arvo joukossa |z| = 1.

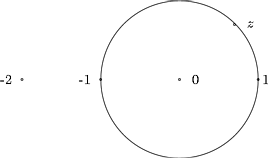
Kuva 24:

|z2+2iz| = |z(z+2i)| = |z||z+2i| = |z+2i| = |z-(-2i)| = d(z1,-2i)
Kolmioepäyhtäl"n perusteella
2 = | |z|-|-2i| | £ |z-(-2i)| £ |z|+|-2i| = 3.
Kun z = i, on |z2+2iz| = 3 eli maksimi.
Kun z = -i, on |z2+2iz| = 1 eli minimi.

Yleisesti epäyhtäl"ssä

| |z1|-|z2| | £ |z1+z2| £ |z1|+|z2|
esiintyy yhtäsuuruus, kun (ja vain kun) z1 ja z2 ovat samalla origon kautta kulkevalla suoralla.
2. Määrää jokin sellainen reaaliluku d > 0, että
|z5+3z2| < 0.1
kun |z| < d. Tämä on tyypillinen e-d -tehtävä.(vrt. seuraava luku.) Tarkastellaan funktion f(z) = z5+3z2 jatkuvuutta origossa. Valitaan e = 0.1. Pyritään l"ytämään d > 0 siten, että
d(z,0) < dŽ |f(z)-f(0)| < 0.1.
|z5+3z2| £ |z|5+3|z|2 £ |z|+3|z| = 4|z|, kun |z| < 1.
4|z| < 0,1, kun |z| < [0,1/4] = 0,025. Valitaan d = 0.025.
3. Olkoot z1, z2, z3 kompleksilukuja. Osoita, että |z1+z2+z3| ³ |z1|-|z2|-|z3|.
Tod.
|z1+z2+z3| \buildrel D-ey
³
| |z1+z2|-|z3| | ³ |z1+z2|-|z3|
\buildrel D- ey
³
| |z1|-|z2| | - |z3| ³ |z1|-|z2|-|z3|.

2.5  Kompleksitason topologia

Pisteen a Ī C r-säteinen ympyräympärist" eli r-ympärist" määritllään joukkona

U(a,r) = { z Ī C \arrowvert  |z-a| < r }.
Piste a on joukon a sisäpiste, jos U(a,r) Ģ A jollakin r > 0. Joukko A Ģ C on avoin, jos jokainen piste a Ī A on a:n sisäpiste.

Joukko F Ģ C on suljettu, jos sen komplementti C\F on avoin. Komplementille ei ole vakiintunut hyvää merkintää. Voimme käyttää esimerkiksi merkintää C(F) = C\F.

Esimerkkejä avoimista joukoista:
(i) C ja Ę ovat avoimia
(ii) Kiekko D = { z  \arrowvert |z-z0| < r } on avoin
(iii) Punkteerattu taso

Ca¢ = {z Ī C \arrowvert  z ¹ a }
on avoin. (Merkintä Ca¢ ei ole aivan yleisesti käyt"ssä.)

Esimerkkejä suljetuista joukoista:
(i) C ja Ę ovat suljettuja
(ii) Suljettu kiekko [`(D)] = { z  \arrowvert  |z-z0| £ r } on suljettu
(iii) Yksi"t { a } ovat suljettuja.

Olkoon A Ģ C. Komplementin C(A) sisäpisteitä sanotaan A:n ulkopisteiksi. Jos piste ei ole A:n sisä- eikä ulkopiste, niin se on A:n reunapiste. Olkoon
IntA = A:n sisäpisteiden joukko
ExtA = A:n ulkopisteiden joukko
BdA = A:n reunapisteiden joukko.
Silloin jokaiselle joukolle A on voimassa

C = IntA ČExtA ČBdA.
Joukot IntA, ExtA ja BdA ovat pistevieraita. Niistä kaksi voi olla tyhjiä joukkoja.

Esimerkki. A = { x+iy  \arrowvert  x,y Ī Q}. Silloin IntA = ExtA = Ę ja BdA = C.

Joukko [`(A)] = A ČBdA on A:n sulkeuma. Joukot IntA ja ExtA ovat avoimia ja [`(A)] ja BdA suljettuja.

Joukko A on pisteen a ympärist", jos a Ī IntA.

Piste a on joukon A kasaantumispiste, jos jokainen a:n ympärist" sisältää a:sta eroavan A:n pisteen.

2.6  Pistejonon suppeneminen

Olkoon z1,z2,¼ = (zn) kompleksitason (päättymät"n) pistejono. Jonoa sanotaan suppenevaksi ja kompleksilukua z sen raja-arvoksi, jos jokaista z:n ympärist"ä U vastaa n0 Ī N siten, että

n > n0 Ž zn Ī U.
Täll"in merkitään z = limn ® „ zn.

Määritelmässä voidaan rajoittua r-ympärist"ihin U(z,r).

Itse asiassa limn ® „|zn-z| = 0.

Esimerkkejä.
1. limn ® „ [(in+1)/(n+i)] = i, sillä (kun n > 1)

ź
ź
ź 		in+1
n+i
 -i ź
ź
ź 		= ź
ź
ź 		in+1-in+1
n+i
 ź
ź
ź 		= 2
|n+i|
 £ 2
n-1
 < r,  kun  n > 1+ 2
r
 .
Laskut sujuivat siis hyvin samalla tavalla kuin reaalisten jonojen tapauksessa.
2.Olkoon zn = xn+iyn ja z = x+iy. Silloin

lim
n ® „ 
 zn = z Ū ģ
ļ
ļ
ķ
ļ
ļ
ī

lim
n ® „ 
 xn = x

lim
n ® „ 
 yn = y
Tod.a)
Oletus: limn ® „zn = z.
Väite: limn ® „xn = x ja limn ® „ = y.
Tod: Koska (D-ey) |xn-x| £ |zn-z| ja |yn-y| £ |zn-z|, on limn ® „xn = x ja limn ® „yn = y.
b)
Oletus: limn ® „xn = x ja limn ® „yn = y.
Väite: limn ® „zn = z.
Tod: Olkoon r > 0. Täll"in on olemassa n0 Ī N siten, että
n > n0 Ž |xn-x| < r
Ö2
   ja  |yn-y| < r
Ö2
 .
Mutta silloin on
|zn-z| =   _____________
Ö(xn-x)2+(yn-y)2
 
 <   ę
 ś
Ö
r2
2
 + r2
2
 
 = r
arvoilla n > n0. Siis limn ® „zn = z.

Kompleksisille jonoille ovat voimassa summan, tulon ja osamäärän raja-arvoa koskevat säänn"t.

Cauchyn konvergenssikriteerio. Jono (zn) suppenee aina ja vain, kun jokaista positiivilukua e vastaa kokonaisluku ne siten, että

|zn+p-zn| < e,  kun  n > ne   ja  p ³ 0.
Todistus.
a) Olkoon jono (zn) suppeneva, sen raja-arvo z ja e > 0. Silloin on olemassa luku ne siten, että
n > ne Ž |zn-z| < e
2
 .
Olkoot p ³ 0 ja n > ne kokonaislukuja. Koska p+n > ne ja n > ne, on
|zn+p-z| < e
2
   ja  |zn-z| < e
2
 .
Mutta täll"in
|zn+p-zn| = |(zn+p-z)-(zn-z)| £ |zn+p-z|+|zn-z| < e
2
 + e
2
 = e.
b) Olkoon lauseen ehto voimassa. Merkitään zn = xn+iyn. Koska
|xn+p-xn|
£
|zn+p-zn|,
|yn+p-yn|
£
|zn+p-zn|,
ovat (xn) ja (yn) reaalisia Cauchyn jonoja. On siis olemassa x = limn ® „xn ja y = limn ® „yn. Täll"in limn ® „zn = z = x+iy.

Esimerkki. Osoitetaan, että suppeneva jono (zn) on rajoitettu.

Olkoon z = limn ® „zn. Valitaan r = 1. Silloin on olemassa n1 siten, että

zn Ī U(z,1),  kun  n > n1.

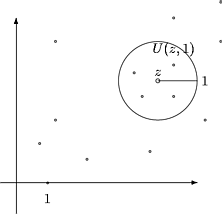
Kuva 25:

Arvoilla n > n1 on siis

|zn| = |zn-z+z| £ |zn-z|+|z| < |z|+1.
Olkoon M = max{|z1|, |z2|, ¼, |zn1|, |z|+1 }. Silloin
|zn| £ M     kaikille  n = 1,2, ¼,
eli zn Ī U(0,M) kaikille n = 1,2,¼.