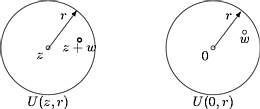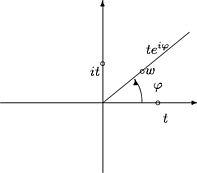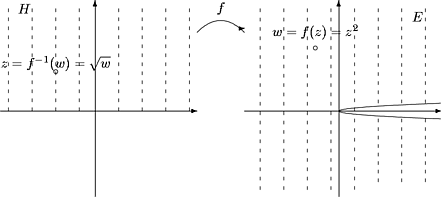3 Analyyttiset funktiot

3.1 Kompleksimuuttujan kompleksiarvoinen funktio

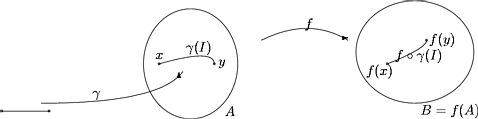
Olkoot A ja B kompleksitason C osajoukkoja. Kuvausta

f:A ® B

sanotaan kompleksimuuttujan kompleksiarvoiseksi funktioksi. Usein on B = C.

1.Vakiokuvaus. Esimerkiksi kuvaus f:C® C, f(z) = 1 "z Î C on kompleksimuuttujan kompleksiarvoinen funktio. Yleisesti olkoon A Ì C ja a Î C. Silloin kuvaus f:A ® C,

f(z) = a "z Î A

on vakiofunktiona kompleksimuuttujan kompleksiarvoinen funktio.

2.Identtinen kuvaus. Olkoon A Ì C ja f(z) = z "z Î A. Silloin f:A ® A on joukon A identtinen kuvaus.

3. Muotoa

S(z) =

az+b

cz+d

;a,b,c,d Î C

olevia kuvauksia sanotaan M"bius-kuvauksiksi. Jos valitaan a = d = 1 ja b = c = 0, on S(z) = z eli S: C® C on identtinen kuvaus. Jos ad-bc = 0 ja |c|+|d| ¹ 0 (eli cz+d ¹ 0), S on vakiokuvaus: Jos c ¹ 0, on

S(z) =

acz+bc

c(cz+d)

acz+ad

c(cz+d)

a(cz+d)

c(cz+d)

Jos d ¹ 0, on vastaavasti

S(z) =

adz+bd

d(cz+d)

bcz+bd

d(cz+d)

b(cz+d)

d(cz+d)

Olkoon D = ad-bc ¹ 0. Erotetaan kaksi tapausta:
a) c ¹ 0. Kuvaus S(z) = [(az+b)/(cz+d)] on määritelty, kun cz+d ¹ 0 eli kun z ¹ -^d/_c. Kuvaus on bijektio

ì
í
î

ü
ý
þ

® C\

ì
í
î

ü
ý
þ

sillä yhtäl"llä

az+b

cz+d

= w

az+b = cwz+dw

(a-cw)z = dw-b

z =

dw-b

a-cw

on täsmälleen yksi ratkaisu z, kun w ¹ ^a/_c. (Voidaan jo nyt havaita, että S(-^d/_c) = ¥ ja S(¥) = ^a/_c. Kuvaus S on siis bijektio CÈ{ ¥} ® CÈ{ ¥}.
b) c = 0. Koska ad-bc ¹ 0, on d ¹ 0. Kuvaus

S(z) =

az+b

cz+d

az+b

on nyt määritelty kaikille z Î C. Kuvaus on bijektio C® C, sillä

az+b

= w

az = dw-b

z =

dw-b

(koska ad-bc ¹ 0 ja c = 0, on a ¹ 0). (Tässä tapauksessa S(¥) = ¥, joten S:CÈ{ ¥} ® CÈ{ ¥} on bijektio.)

4. Määritellään f:C® C asettamalla

f ( re^ij ) =

r+1

e^ij, f(0) = 0.

Koska kuvaus r ® [(r)/(r+1)] on bijektio ]0,¥[ ® ]0,1[ on

f:C® U(0,1)

bijektio. Jos merkitään z = re^ij, on r = |z|. Täll"in

f(z) =

1+r

re^ij =

1+|z|

Kuvaus f(z) = [(z)/(1+|z|)] on siis bijektio C® U(0,1).

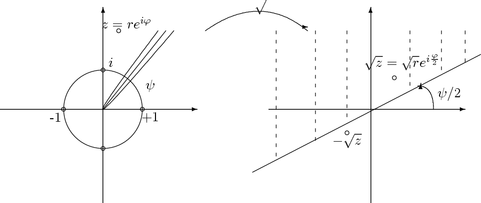
5. Neli"juuri. Tarkastellaan kuvausta f:z ® z². Binomiyhtäl"llä z² = w on kaksi ratkaisua, joille käytetään merkint"jä Öw ja -Öw. Jos w = re^ij, niin

Öw = Öre^i[(j)/2] ja -Öw = Öre^i([(j)/2]+p) = -Öre^i[(j)/2].

Kuvaus f:C® C on siis surjektio, mutta ei injektio, sillä pisteille w ¹ 0 kuvautuu aina kaksi pistettä

z₁ = Öw ja z₂ = -Öw.

(On huomattava, että ei ole mitään yleistä tapaa erottaa, kumpi neli"juurista on z₁ ja kumpi z₂. Jos toista merkitään Öw:llä, niin toinen on -Öw.)

Olkoon A = {z | Im z > 0 } ja B = C\{z | Im z = 0, Re z ³ 0 }. Silloin f:A ® B on bijektio. Sen käänteiskuvausta f^-1:B ® A sanotaan neli"juuren haaraksi, joka on määritelty pitkin positiivista reaaliakselia aukileikatussa tasossa.

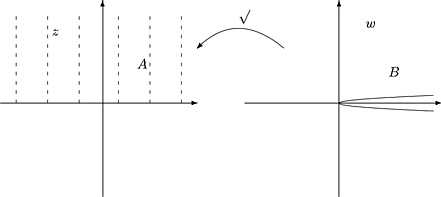
Kuva 26:

Neli"juuri voidaan määritellä jokaisessa origoon päättyvää sädettä pitkin aukileikatussa tasossa. Neli"juuri on yksikäsitteinen, kun sovitaan, miten taso aukileikataan ja kumpaan puolitasoon kuuluva haara valitaan. Ennen kuin voidaan ollenkaan puhua neli"juuresta, on valittava tason aukileikkaus.

Kuva 27:

Esimerkki. Mitä vikaa on seuraavassa päättelyssä?

-1

__
Ö-1

æ
ú
Ö

-1

æ
ú
Ö

-1

__
Ö-1

Ö1

__
Ö-1

æ
è

__
Ö-1

ö
ø

( Ö1 )²

-1

Kuva 28:

Jos Ö määritellään siten, että se kuvaa aukileikatun tason ylemmälle vinolle puolitasolle I, niin -Ö kuvaa sen alemmalle puolitasolle II.
Onko Ö[(-1)] = [(Ö1)/(Ö[(-1)])] ?
Ei ole, sillä Ö[(-1)] = i, Ö1 = 1 ja ¹/_i = -i.
Onko sitten -Ö[(-1)] = [(-Ö[(-1)])/(-Ö1)] ?
Ei ole, sillä -Ö[(-1)] = -i ja -Ö1 = -1 sekä [(-i)/(-1)] = i ¹ -Ö[(-1)].

Haaralle I on siis Ö[(-1)]_I ¹ [(Ö1_I)/(Ö[(-1)]_I)] ja haaralle II on siis Ö[(-1)]_II ¹ [(Ö[(-1)]_II)/(Ö1_II)]. Yhtäl"ä

__
Ö-1

Ö1

__
Ö-1

ei siis voida johtaa yhtäl"stä Ö[(-1)] = Ö[(-1)], määriteltiinpä neli"juuri miten hyvänsä.

Voidaan huomata, että

__
Ö-1

Ö1

ja -

__
Ö-1

-Ö1

__
Ö-1

sillä

i =

ja -i =

-1

-i

Siis

__
Ö-1

Ö1

pätee haaralle I, mutta ei haaralle II.

__
Ö-1

Ö1

__
Ö-1

pätee haaralle II, mutta ei haaralle I.
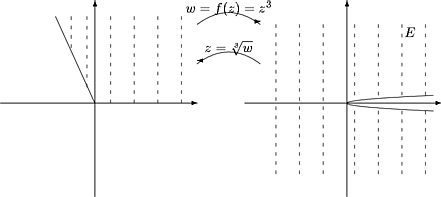
6. Kuutiojuuri. Kuvaus f(z) = z³ on injektio esimerkiksi alueessa 0 < argz < [(2p)/3]. Sen kuva on pitkin positiivista reaaliakselia aukileikattu taso. Kuutiojuurella on tässä alueessa kolme haaraa, joiden kuvana ovat alueet

I: 0 < argz <

II:

< argz <

III:

< argz < 2p

Yleisesti voidaan määritellä ⁿÖ{w}, n = 2,3,4,¼.

Kuva 29:

Kuva 30:

Esimerkki. Määrää suoran z+[`(z)]-1 = 0 kuva M"bius-kuvauksessa S(z) = [(z+1)/(z)].
Mikä suora? Yleinen tapa: x-akselin leikkauspisteessä on z = [`(z)] = x. Siis 2x = 1 eli x = ¹/₂. y-akselin leikkauspisteessä on z = iy, [`(z)] = -iy. Siis iy-iy-1 = 0 ei toteudu. Kyseessä on siis suora x = ¹/₂.

w =

z+1

zw = z+1

z(w-1) = 1

z =

w-1

Kuvan yhtäl":

w-1

-1

-1+w-1-(

-1)(w-1)

+w-2-w

+w-1

-2w-2

Ympyrä: z[`(z)]+az+b[`(z)]+g = 0, a = [`(b)], g < ab
a = b = -2, g = 3, 3 < (-2)(-2) = 4.
Jos a = a-ib ja b = a+ib, niin keskipiste on (-a,-b) ja säde Ö{a²+b²-g}.
Kuvana on siis ympyrä, jonka keskipiste on (2,0) ja säde on 1. Saamme erikoistapauksen yleisestä tuloksesta: M"bius-kuvaus kuvaa suoran ympyräksi (tai suoraksi).

Yleisesti suoran x = n yhtäl" kompleksimuodossa on

2n = 2x = 2Re z = z+

eli

-2n = 0.

Vastaavasti suoran y = n yhtäl" kompleksimuodossa on

2in = 2iy = z-

eli

-2in = 0.

Kertomalla i:llä saadaan yhtäl" normaalimuotoon az+b[`(z)]+g = 0, a = [`(b)] ja g Î R:

iz-i

+2n = 0.

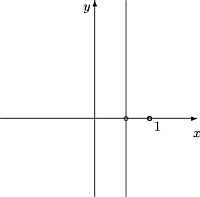
3.2 Kuutiojuuri reaalifunktiona ja kompleksifunktiona

Kuva 31: Funktion x ® x³ kuvaaja

Kuvaus f:x ® ³Ö{x} on määritelty kaikille x Î R. Sen derivaatta

f¢(x) =

3x^²/₃

on määritelty kaikille x ¹ 0. Arvolla x = 0 käyrän tangentti on pystysuora eikä funktiolla ole äärellistä derivaattaa. Jatkossa nähdään, että jo tämä riittää osoittamaan, ettei reaalista kuutiojuurta voida luonnollisella tavalla jatkaa kompleksifunktioksi.

Tarkastellaan kuutiojuurta kompleksifunktiona. Otetaan määrittelyjoukoksi pitkin negatiivista imaginaariakselia aukileikattu taso A = C\{ z | Re z = 0, Im z £ 0 } = C\{ z | argz = [(3p)/2] }.

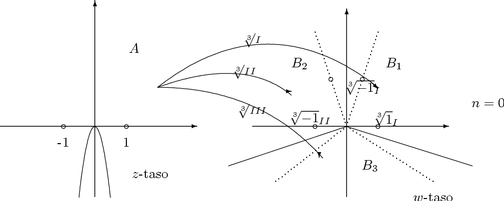
Kuva 32:

Kuutiojuurella on A:ssa kolme haaraa, joiden maaleina ovat sektorialueet

B₁

ì
í
î

w Î C

ê
ê

< argw <

ü
ý
þ

n = 0

B₂

ì
í
î

w Î C

ê
ê

< argw <

ü
ý
þ

n = 1

B₃

ì
í
î

w Î C

ê
ê

< argw <

11p

ü
ý
þ

n = 2

Kuutiojuuren haarat ovat:

3 æ
Ö

A ® B₁

3 æ
Ö

A ® B₂

3 æ
Ö

III

A ® B₃

³Ö{ }_I kuvaa positiivisen reaaliakselin positiiviselle reaaliakselille ja negatiivisen reaaliakselin suoralle argw = [(p)/3].
³Ö{ }_II kuvaa positiivisen reaaliakselin suoralle argw = [(2p)/3] ja negatiivisen reaaliakselin negatiiviselle reaaliakselille (argw = [(3p)/3]).
³Ö{ }_III kuvaa positiivisen reaaliakselin suoralle argw = [(4p)/3] ja negatiivisen reaaliakselin suoralle argw = [(5p)/3].

Reaalinen kuutiojuuri f saadaan siis ottamalla ³Ö{ }_I positiivisella reaaliakselilla ja ³Ö{ }_II negatiivisella reaaliakselilla ja määrittelemällä f(0) = 0.

3.3 Funktion raja-arvo

Olkoot A ja B kompleksitason joukkoja ja f:A ® B kuvaus. Kuvauksella f on pisteessä z₀ Î [`(A)] raja-arvo c, jos jokaista e > 0 vastaa d > 0 siten, että

0 < |z-z₀| < d ja z Î A Þ |f(z)-c| < e.

Raja-arvoa varten riittää tarkastella jonoja z_n ® z₀, z_n Î A\{z₀}. Funktiolla on raja-arvo c, jos ja vain jos kaikille tällaisille jonoille on voimassa

lim
n ® ¥

f(z_n) = c.

Esimerkki.

f(z) =

Re z

on määritelty joukossa A = C\{0} ja 0 Î [`(A)]. Onko olemassa raja-arvoa

lim
z ® 0

f(z) ?

Olkoon z_n = ¹/_n. Silloin Re z_n = ¹/_n = z_n ja f(z_n) = [(Re z)/(z)] = 1, joten lim_{n ® ¥} f(z_n) = 1, limz_n = 0.
Olkoon z_n = ⁱ/_n. Silloin Re z_n = 0 ja f(z_n) = 0, joten lim_{n ® ¥} f(z_n) = 0, lim z_n = 0. Raja-arvoa ei siis ole olemassa.

Funktio f on jatkuva pisteessä z₀ Î A, jos

lim
z ® z₀

f(z) = f(z₀).

Kuvaus f on jatkuva joukossa A, jos se on jatkuva jokaisessa A:n pisteessä. Oletetaan, että A on avoin joukko. Silloin f:A ® B on jatkuva, jos ja vain jos jokaisen avoimen joukon U Ì C alkukuva f^-1(U) on avoin. Funktio f = u+iv on jatkuva, jos ja vain jos u:A ® R ja v:A ® R ovat jatkuvia.

Olkoon I = [0,1] yksikk"väli. Polulla g tarkoitetaan jatkuvaa kuvausta

g: I ® C

g(0) polun alkupiste
g(1) polun loppupiste
g(I) polun kantaja eli jälki.

Jos g(I) Ì A, niin g on joukon A polku. Pisteet g(0) ja g(1) on täll"in yhdistetty polulla g joukossa A.

Jos A:n kaksi pistettä voidaan aina yhdistää polulla A:ssa, niin A on polkuyhtenäinen. Jos A on lisäksi avoin, niin A on alue. Esimerkiksi joukko {z | Im z = 0 } on polkuyhtenäinen, mutta se ei ole avoin. Sen sijaan esimerkiksi yksikk"kiekko U(0,1) on sekä avoin että polkuyhtenäinen, eli siis alue.

Polkuyhtenäisen joukon kuva jatkuvassa kuvauksessa on polkuyhtenäinen.

Kuva 33:

3.4 Analyyttinen funktio

Olkoon f: G ® C kuvaus, G Ì C. Jotta voisimme derivoida, joudumme olettamaan, että G on avoin joukko. Integrointia varten joudumme olettamaan, että G on polkuyhtenäinen. Avoimet ja yhtenäiset joukot ovat alueita. Jatkossa oletamme siis yleensä, että funktioden määrittelyjoukot ovat alueita.

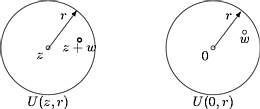
Kuva 34:

Olkoon G alue ja z Î G. Täll"in on olemassa r > 0 siten, että

U(r,z) = { z+w | |w| < r } Ì G.

Funktio

h(w) =

f(z+w)-f(z)

on määritelty punkteeratussa kiekossa

U¢(0,r) = { w | 0 < |w| < r } = U(0,r) \{0}

ja 0 on U¢(0,r):n kasautumispiste. Edellä olleen määritelmän mukaisesti voidaan tutkia raja-arvoa

a =

lim
w ® 0

h(w) =

lim
w ® 0

f(z+w)-f(z)

olemassaoloa. Jos tämä raja-arvo on olemassa, niin f on differentioituva pisteessä z ja luku a = f¢(z) on f:n derivaatta tässä pisteessä.

Funktio, joka on differentioituva alueen G jokaisessa pisteessä, on analyyttinen G:ssä.

Analyyttisyyden määritelmä on erittäin vahva. Siitä seuraa mm., että my"s f¢ on analyyttinen, jolloin edelleen f¢¢ on analyyttinen jne. Analyyttisellä funktiolla on siis kaikkien kertalukujen derivaatat.

Funktio on analyyttinen pisteessä z, jos se on analyyttinen jossakin tämän pisteen ympärist"ssä.

Kompleksifunktion derivaatan määrittely erotusosamäärän avulla on mahdollista, koska kompleksiluvut voidaan jakaa keskenään. Jos tarkastellaan vektorimuuttujan x Î Rⁿ vektoriarvoisia funktioita f:Rⁿ ® Rⁿ, niin derivaatan määrittely tällä tavalla ei onnistu, kun n ³ 3. Tämä johtuu siitä, että lukualuetta ei voida laajentaa tasoa useampiulotteiseksi. (Hamilton ja kvaternionit 1844.)

Kirjoitetaan

e(w) =

f(z+w)-f(z)

- a.

Silloin

f(z+w)-f(z) = aw+w e(w),

(8)

joten a on funktion f derivaatta pisteessä z, jos ja vain jos kehitelmä (8) pätee ja e(w) ® 0, kun w ® 0. Tätä kautta kompleksinen derivaatta a = f¢(z) ja Analyysi4:n yleinen derivaatta (lineaarikuvauksena) liittyvät toisiinsa.

Esimerkkejä. 1. Vakiokuvaus f(z) = c on analyyttinen koko tasossa ja f¢(z) º 0, sillä

f(z+w)-f(z) = 0·w+w·0.

Tässä 0 = f¢(z) ja e(w) º 0.
2. Identtinen kuvaus f(z) º z on analyyttinen koko tasossa ja f¢(z) º 1, sillä

f(z+w)-f(z) = w = 1·w+w·0.

Tässä 1 = f¢(z) ja e(w) º 0.
3. Funktio f(z) = z² on analyyttinen koko tasossa ja f¢(z) = 2z, sillä

f(z+w)-f(z) = (z+w)²-z² = z²+2zw+w²-z² = 2z ·w + w ·w.

Tässä f¢(z) = 2z ja e(w) = w ® 0, kun w ® 0.
4. Funktiolla f(z) = [`(z)] ei ole derivaattaa missään pisteessä z Î C.
Todistus. Tarkastellaan erotusosamäärää

f(z+w)-f(z)

säteillä

ì
í
î

w = t

,t > 0

w = it

, t > 0

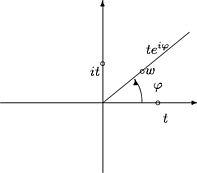
Kuva 35:

f(z+w)-f(z)

1, kun w = t > 0

f(z+w)-f(z)

-it

= -1, kun w = it, t > 0.

Annetaan t ® 0+. Erotusosamäärällä on eri raja-arvot (1 ja -1) näillä säteillä, joten sillä ei ole raja-arvoa kompleksitason topologiassa. On mielenkiintoista huomata, että erotusosamäärällä on raja-arvo jokaisella origosta lähtevällä w-tason säteellä w = te^{i j} :

f(z+w)-f(z)

te^-ij

te^ij

e^-21j = cos2j-isin2j.

Jokaisella origon kautta kulkevalla suoralla saadaan eri raja-arvo.

Kehitelmän (8) avulla voidaan tavalliseen tapaan perustella summan, tulon, osamäärän, käänteisfunktion ja yhdistetyn funktion derivointikaavat kompleksifunktioille. Esimerkiksi, jos

f₁(z+w)-f₁(z)

a₁ w+we₁(w),

f₂(z+w)-f₂(z)

a₂ w+we₂(w),

niin

(f₁+f₂)(z+w)-(z₁+f₂)(z) = (a₁+a₂)w+w(e₁(w)+e₂(w)),

joten

(f₁+f₂)¢(z) = f₁¢(z)+f₂¢(z).

Käänteisfunktion derivaatta: Oletetaan, että funktiolla f on pisteessä z derivaatta f¢(z) ¹ 0 ja että käänteisfunktio f^-1 on määritelty ja jatkuva eräässä pisteen w = f(z) ympärist"ssä V. Silloin f^-1 on differentioituva pisteessä w ja

( f^-1 )¢(w) =

f¢(z)

f¢( f^-1(w) )

Todistus. (Huomaa merkinnän muuttuminen. Nyt on w = f(z). Merkitään siksi z:n lisäystä h:lla.)

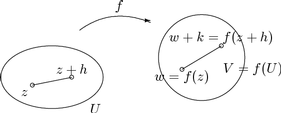
Kuva 36:

f:n jatkuvuuden nojalla k ® 0, kun h ® 0, f:U ® V jatkuva bijektio, jonka käänteiskuvaus f^-1:V ® U on jatkuva ja f^-1:n jatkuvuuden nojalla h ® 0, kun k ® 0. Jos w+k Î V, k ¹ 0, niin merkitään f^-1(w+k) = z+h. Silloin h ¹ 0 ja

f^-1(w+k)-f(w)

z+h-z

f(z+h)-f(z)

f¢(z)h+he(h)

f¢(z)+e(h)

f¢(z)

, kun k ® 0.

Esimerkki. Funktio f(z) = z²

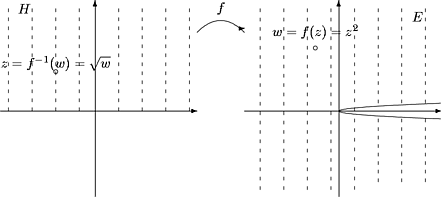
Kuva 37:

on injektio ylemmässä puolitasossa H = { z | Im z > 0 } ja E = f(H) on pitkin positiivista reaaliakselia aukileikattu taso C\[0, ¥[. Neli"juuri voidaan määritellä kuvauksena f^-1:E ® H. Merkitään

f^-1(w) = Öw.

Osoitetaan, että f^-1 on jatkuva E:ssä. Olkoon w₁, w₂ Î E ja

z₁

x₁+iy₁ =

__
Öw₁

z₂

x₂+iy₂ =

__
Öw₂

jolloin y₁ > 0 ja y₂ > 0. Saadaan arvio

|w₂-w₁|

| z₂²-z₁²| = |z₂-z₁||z₁+z₂| = |z₂-z₁|

_______________
Ö(x₁+x₂)²-(y₁+y₂)²

|z₂-z₁|(y₁+y₂) > y₁|z₂-z₁|,

mistä saadaan

|z₂-z₁| <

|w₂-w₁|

y₁

Pidetään w₁ (ja siis my"s y₁) vakiona ja annetaan w₂ ® w₁. Silloin |w₂-w₁| ® 0, joten my"s

|z₂-z₁| =

ê
ê

__
Öw₂

__
Öw₁

ê
ê

® 0.

Näin ollen Öw on jatkuva pisteessä w₁. Koska w₁ (ja w₂) valittiin mielivaltaisesti E:stä, on Öw jatkuva E:ssä.

Käänteisfunktion derivaattaa koskevasta tuloksesta seuraa, että Öw on derivoituva E:ssä ja sen derivatta on

f¢(z)

f¢(Öw)

2Öw

sillä f(z) = z² ja f¢(z) = 2z.

Vastaavalla tavalla nähdään, että kuutiojuuri on jatkuva E:ssä ja sen derivaatta on

f¢(z)

f¢(

3 æ
Ö

)

3 æ
Ö

)²

Tulos yleistyy n:teen juureen ⁿÖ{w}.

Kuva 38:

3.5 Cauchy-Riemannin -yhtäl"t

Olkoon f:A ® C kuvaus ja z Î A joukon A sisäpiste. Oletetaan, että f on differentioituva pisteessä z = x+iy, jolloin

f(z+w)-f(z) = a ·w + w ·e(w),

(9)

missä e(w) ® 0, kun w ® 0. Hajotetaan kaikki termit reaali- ja imaginaariosiinsa:

f(z)

u(x,y)+iv(x,y)

a+ i b

h+ik

e(w)

e₁(w)+ie₂(w).

Yhtäl" (9) hajoaa täll"in kahdeksi reaaliseksi yhtäl"ksi:

u(x+h,y+k)-u(x,y)

ah-bk+he₁(w)-ke₂(w)

v(x+h,y+k)-v(x,y)

bh+ak+ke₁(w)+he₂(w).

Koska

|he₁(w)-ke₂(w)|²

|(h,k) ·(e₁(w),e₂(w))|²

\buildrel Schwarzin ey.

||(h,-k)||² || (e₁(w),e₂(w)) ||² = (h²+k²)(e₁(w)²+e₂(w)²),

lim
Ö[(h²+k²)] ® 0

h e₁(w)-ke₂(w)

_____
Öh²+k²

= 0.

Näin ollen funktio u:A ® R on (Analyysi 3:n ja Analyysi 4:n mielessä) differentioituva pisteessä z = (x,y) ja

D₁u

u_x = a,

D₂u

u_y = -b.

Samalla perusteella v:A ® R on differentioituva pisteessä z = (x,y) ja

D₁v

v_x = b,

D₂v

v_y = a.

Funktiot u ja v toteuttavat siis ns. Cauchy-Riemannin differentiaaliyhtäl"t

ì
í
î

u_x = v_y

u_y = -v_x.

(10)

Oletetaan kääntäen, että funktiot u:A ® R ja v:A ® R ovat differentioituvia joukon A sisäpistessä z = (x,y) ja toteuttavat tässä pisteessä Cauchy-Riemannin differentiaaliyhtäl"t (10). Muodostetaan funktio f = u+iy: A ® C.

Väite: f on differentioituva pisteessä z ja f¢(z) = u_x(x,y)+iv_x(x,y) = v_y(x,y)-u_y(x,y).
Todistus: Differentioituvuuden määritelmän perusteella u:lla ja v:llä on kehitelmät

u(x+h,y+k)-u(x,y)

u_x(x,y)h+u_y(x,y)k+|w|e₁(w)

v(x+h,y+k)-v(x,y)

v_x(x,y)h+v_y(x,y)k+|w|e₂(w),

missä w = h+ik ja e_j ® 0, kun w ® 0, j = 1,2,¼. Yhtäl"iden (10) nojalla on

f(z+w)-f(z)

u_xh+u_yk+iv_xh+iv_yk+|w| e₁(w)+i|w|e₂(w)

u_xh+iv_yk+i(v_xh-iu_yk)+|w|e₁(w)+i|w|e₂(w)

u_xh+iu_xk+i(v_xh+iv_xk)+|w|(e₁(w)+ie₂(w))

u_x(h+ik)+iv_x(h+ik)+|w|(e₁(w)+ie₂(w))

(u_x+iv_x)w+w

|w|

(e₁(w)+ie₂)).

Merkitään

u_x(x,y)+iv_x(x,y)

e(w)

|w|

(e₁(w)+ie₂(w)).

Silloin

f(z+w)-f(z) = aw+we(w),

missä e(w) ® 0, kun w ® 0.

On siis todistettu

Lause 2 Funktio f = u+iv:G ® C on analyyttinen alueessa G, jos ja vain jos funktiot u:G ® R ja v:G ® R ovat G:ssä differentioituvia ja toteuttavat Cauchy-Riemannin yhtäl"t (10).

Oletetaan, että olemme unohtaneet Cauchy-Riemannin yhtäl"t. Miten ne voidaan palauttaa mieleen? Oletetaan, että derivaatta

f¢(z) =

lim
w ® 0

f(z+w)-f(z)

on olemassa pisteessä z Î G. Valitaan w:lle sopivia teitä lähestyä nollaa, w = h+ik = (h,k), z = x+iy = (x,y):
1) w menee reaalisena kohti nollaa. Merkitään w = h = (h,0)

f(z+w)-f(z)

u(x+h,y)+iv(x+h,y)u(x,y)-iv(x,y)

u(x+h,y)-u(x,y)

v(x+h,y)-v(x,y)

u_x(x,y)+iv_x(x,y) = f¢(z).

2) w menee puhtaasti imaginaarisena kohti nollaa. Merkitään w = ik = (0,k).

f(z+w)-f(z)

u(x,y+k)+iv(x,y+k)-u(x,y)-iv(x,y)

-i

u(x,y+k)-u(x,y)

i(v(x,y+k)-v(x,y))

-iu_y(x,y)+v_y(x,y) = v_y(x,y)-iu_y(x,y) = f¢(z).

Oletetaan, että f¢(z) on olemassa. Kohdassa 1 on f:n osittaisderivaatta x:n suhteen:

f_x(x,y) =

lim
h ® 0

f(z+h)-f(z)

= f¢(z), h Î R.

Kohdassa 2 on f:n osittaisderivaatta y:n suhteen vakiolla kerrottuna:

f_y(x,y)

lim
k ® 0

f(z+ik)-f(z)

lim
k ® 0

i(f(z+ik)-f(z))

lim
k ® 0

f(z+ik)-f(z)

= if¢(z).

Siis f_x(x,y) = ¹/_if_y(x,y) = -if_y(x,y). Saadaan Cauchy-Riemannin yhtäl"iden kompleksimuoto

f_x = -if_y.