4 Alkeisfunktioita

4.1 Eksponenttifunktio

Eksponenttifunktio exp: RŽ R on määritelty kehitelmällä

exp(x) = e^x =

Ľ
ĺ
n = 0

xⁿ

Pyrimme laajentamaan määritelmän koko tasoon C siten, että
1^° exp:CŽ C on analyyttinen ja
2^° exp(x) = e^x, kun x Î R.
Itse asiassa tiedämme jo vastauksen Eulerin kaavasta:

e^z = e^x+iy = e^xe^iy = e^x(cosy+isiny).

Asetetaan

ě
í
î

u(x,y) = e^xcosy,

v(x,y) = e^xsiny

ja määritellään (z = x+iy)

e^z = u+iv = e^x(cosy+isiny).

(11)

Funktio exp(z) = e^z toteuttaa ehdon 2^°, sillä jos y = 0, on z = x Î R ja

e^x = e^x(cos0+isin0).

Ehdon 1^° todistaminen on helppoa edellisen lauseen avulla: Funktiot u ja v ovat differentioituvia koko tasossa ja

u_x(x,y)

e^xcosy,

u_y(x,y)

-e^xsiny,

v_x(x,y)

e^xsiny,

v_y(x,y)

e^xcosy,

joten u_x = v_y ja u_y = -v_x eli Cauchy-Riemannin yhtälöt toteutuvat. Kaavalla (11) määritelty funktio

exp(z) = e^z

on siis analyyttinen koko tasossa.

Voidaan osoittaa, että jos f:CŽ C on jokin analyyttinen funktio, jolle

f(x) = e^x, kaikille x Î R,

niin, f(z) = e^z kaikille z Î C. Ehdot 1^° ja 2^° määräävät siis funktion exp yksikäsitteisesti. Eksponenttifunktion ominaisuuksia

1. Derivoimiskaava: Edellä osoitettiin, että

f˘(z) = u_x(x,y)+iv_x( x,y).

Näin ollen

exp˘(z) = e^xcosy+iesiny = e^x(cosy+isiny) = exp(z).

Tuttu derivoimiskaava pätee siis koko tasossa C.
2.Eulerin kaava e^ij = cosj+isinj on e^z:n määritelmän erikoistapaus (valitaan z = ij).
3. Määritelmä e^z = e^x(cosy+isiny) voidaan kirjoittaa muotoon

e^z = e^xe^iy,

joten | e^z | = e^x ja arge^z = y.

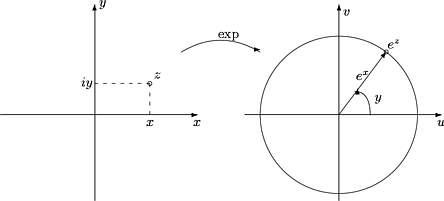Kuva 38:

Kun z liikkuu pitkin y-akselin suuntaista suoraa, e^z kiertää pitkin origokeskeistä ympyrää, jonka säde on e^x.
4. Yhteenlaskukaava:

e^z₁e^z₂ = e^z₁+z₂.

5. Kompleksialueessa ilmenee uusi ominaisuus: Eksponenttifunktio on jaksollinen ja sen jakso on 2pi:

exp(z+n2pi) = exp(z)exp(n2pi) = exp(z).

Joukko { z | 0 Ł Im z < 2p} on exp:n jaksovyö.

Lause 3 exp saa jaksovyössä kaikki kompleksiarvot täsmälleen kerran, lukuunottamatta arvoa 0, jota se ei saa lainkaan.

Todistus. Olkoon w = re^ij, r > 0, 0 Ł j < 2p. Silloin

e^z = re^ij

ě
í
î

e^x = r

e^iy = e^ij

ě
í
î

x = lnr

y = j+ n2p, n Î Z.

Piste x+iy on jaksovyössä, jos ja vain jos n = 0. Arvo w š 0 saavutetaan jaksovyössä siis täsmälleen kerran. Koska | e^z | = e^x > 0, ei exp saa arvoa 0 millään z Î C.

exp(z):lla ei ole raja-arvoja 0 eikä Ľ, kun z Ž Ľ. Kumpaakaan näistä kahdesta arvosta exp(z) ei siis saa edes Ľ:ssä.

Määritelmä 1 Olkoot G ja G˘ alueita. Analyyttista bijektiota f:G Ž G˘ kutsutaan konformikuvaukseksi.

Kompleksianalyysin (=funktioteorian) keskeisiä perustehtäviä on ollut kuvata annettu alue G konformisesti toiselle annetulle alueelle G˘. Tämä ei suinkaan ole aina mahdollista, jos alueet G ja G˘ eivät ole riittävän samansukuisia.

Esimerkki. Olkoon G = { z Î C| 0 < Re z < 1 } ja G˘ = { w Î C| Im w > 0 }. Yritetään muodostaa konformikuvaus f: G Ž G˘.

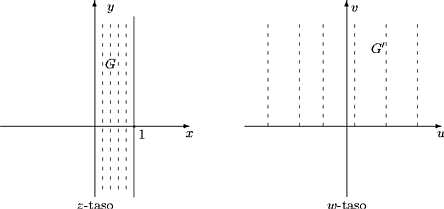Kuva 39:

Eksponenttifunktio kuvaa vaakasuoran viipaleen sektoriksi. Jos viipaleen leveys on p, niin sektori on puolitaso.
Vaiheet:
1. Kierretään G vaakasuoraksi
2. Levennetään G p:n levyiseksi
3. Kuvataan exp:llä puolitasolle

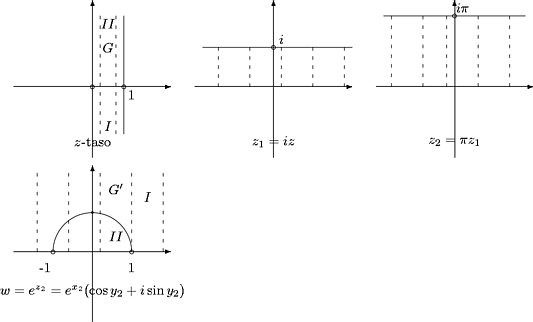Kuva 40:

Haettu konformikuvaus f:G Ž G˘ on siis

f(z) = e^{pi z}.

Kokeillaan reunapisteillä:

z = 0

f(0) = e⁰ = 1

z = 1

f(1) = e^ip = -1.

Jana [0,1] kuvautuu pisteitä 1 ja -1 yhdistäväksi puoliympyräksi.

Kokeillaan sisäpisteellä:

z =

) = e^i[(p)/2] = i.

Janan [0,1] keskipiste kuvautuu puoliympyrän puoliväliin.

Olkoon z = x+iy:

f(z)

e^ipz = e^ip(x+iy) = e^-py+ipx

|f(z)|

e^-py

Jos y < 0, niin e^-py > 1.
Jos y = 0, niin e^-py = 1.
Jos y = 0, niin e^-py < 1.

Siis alueen G ne pisteet, jotka ovat x-akselin alapuolella, kuvautuvat G˘:n pisteille, jotka ovat yksikköympyrän ulkopuolella. Vastaavasti x-akselin yläpuolella olevat G:n pisteet kuvautuvat yksikköympyrän sisäpuolella oleville G˘:n pisteille.

4.2 Logaritmifunktio

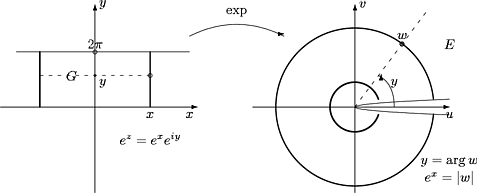Kuva 41:

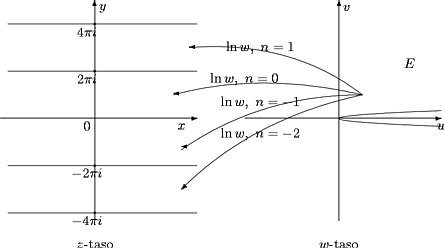
exp on injektio alueessa G = { z | 0 < Im z < 2p}. Tämän alueen kuva on pitkin positiivista reaaliakselia aukileikattu taso E. Käänteiskuvausta exp^-1:E Ž G kutsutaan logaritmifunktion päähaaraksi ja sillä on lauseke

lnw = ln|w|+iargw, 0 Ł argw < 2p,

sillä

e^lnw = e^ln|w|e^iargw = |w|(cos(argw)+isin(argw)) = w.

Koska lnw on jatkuva E:ssä, on

lnw =

ć
ç
č

e^z

ö
÷
ř

z = lnw

Yleisemmin on e^z:n rajoittuma jokaiseen alueeseen n2p < Im z < (n+1)2p, n = 0, ą1,ą2, ź, injektio ja jaksollisuuden takia on kuva-alue aina sama kuin arvolla n = 0 eli E. käänteisfunktiolla on E:ssä lauseke

lnw = ln|w|+iargw+n2pi, 0 Ł argw < 2p

jokaisella arvolla n = 0,ą1,ą2,ź .

Kuva 42:

Logaritmilla on E:ssä äärettömän monta haaraa.

Positiivinen reaaliakseli ei kuulu E:hen. Jos positiivinen reaaliakseli halutaan mukaan logaritmin määritysalueeseen, leikataan w-taso auki (esimerkiksi) pitkin negatiivista reaaliakselia.

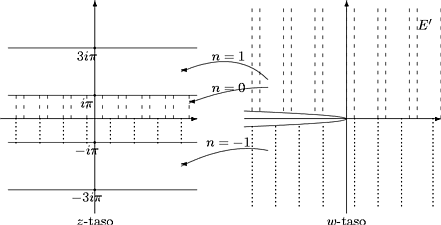Kuva 43:

lnw

ě
í
î

lnw+iargw,

Im w ł 0

lnw+iargw-2pi,

Im w < 0

argw < 2p

Eri haarat saadaan tästä lisäämällä n2pi, n = 0,ą1,ą2,ź.

Logaritmille on voimassa sääntö

ln(z₁+z₂) = lnz₁+lnz₂

vain n2pi:n tarkkuudella.

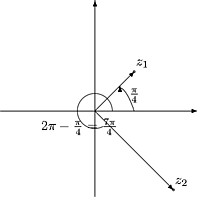
Esimerkkejä 1. Olkoon lnz logaritmin päähaara.

z₁ = -1

lnz₁ = ln|-1|+iarg(-1) = ip

z₂ = -i

lnz₂ = ln|-i|+iarg(-i) = i

z₁z₂ = i

lnz₁z₂ = i

= lnz₁+lnz₂+2pi

2. Olkoon lnz = ln|z|+iargz, 0 Ł argz < 2p logaritmin päähaara ja z₁ = 1+i, z₂ = 2-2i.

Kuva 44:

Silloin

lnz₁

lnÖ2+i

lnz₂

ln2Ö2+i

z₁z₂

2+2+2i-2i = 4

lnz₁+lnz₂

lnÖ2+ln2Ö2+i

= ln4+2pi

lnz₁z₂

ln4.

3. Yhtälön e^z = 3-4i ratkaiseminen.

ln(3-4i)

|3-4i|

____
Ö9+16

= 5

arg(3-4i)

arctan

ć
ç
č

ö
÷
ř

+n2pi

Kuva 45:

4.3 Trigonometriset funktiot

Eulerin kaavan mukaan

e^iy

cosy+isiny,

e^-iy

cosy-isiny,

joten reaalisilla arvoilla y on

ě
ď
ď
ď
ď
í
ď
ď
ď
ď
î

cosy =

( e^iy+e^-iy )

siny =

( e^iy-e^-iy )

Näin ollen meillä on täsmälleen yksi mahdollisuus määritellä sinz ja cosz koko tasossa analyyttisina funktioina.

Määritelmä 2

cosz

e^iz+e^-iz

sinz

e^iz-e^-iz

Siis

coshx =

e^x+e^-x

ja sinhx =

e^x-e^-x

Määritelmästä seuraa, että sinz ja cosz ovat koko tasossa analyyttisiä funktioita ja niiden derivaatat ovat

D(cosz)

( ie^iz-ie^-iz ) =

-1

( e^iz-e^-iz ) = -sinz

D(sinz)

( ie^iz+ie^-iz ) =

( e^iz+e^-iz ) = cosz.

Peruskaavoja.
1.

cos(z₁+z₂)

( e^i(z₁+z₂)+ e^{-i(z₁+z₂)} )

( e^iz₁e^iz₂+ e^-iz₁e^-iz₂ )

cosz₁cosz₂

( e^iz₁+e^-iz₁)

( e^iz₂+e^-iz₂)

(e^iz₁e^iz₂+e^-iz₁e^-iz₂+e^iz₁ e^-iz₂+e^-iz₁ e^iz₂)

sinz₁sinz₂

( e^iz₁-e^-iz₁)

(e^iz₂-e^-iz₂)

( e^iz₁e^iz₂+ e^-iz₁e^-iz₂- e^iz₁e^-iz₂- e^-iz₁e^iz₂)

Siis

cos(z₁ąz₂) = cosz₁cosz₂ -ą(sinz₁sinz₂).

Vastaavalla tavalla voidaan osoittaa, että

sin(z₁ąz₂) = sinz₁cosz₂ącosz₁sinz₂.

cos²z+sin²z = 1.

Todistus.

cos²z+sin²z

( e^iz+e^-iz)²-

(e^iz-e^-iz)²

2 e^ize^-iz+

2 e^ize^-iz = 1.

cos(

-z)

cos

cosz+sin

sinz

sinz.

cos(-z)

cosz

sin(-z)

-sinz

5. Funktioilla cosz ja sinz on ainoastaan jaksot n2p.
Todistus. exp:llä on jaksot n2pi, joten sinillä ja kosinilla on jaksoina n2p, n = 0,ą1,ą2,ź. Osoitamme, että muita jaksoja ei ole. Tarkastellaan funktiota sinz.
a)

sinz = 0

e^iz-e^-iz = 0 Ű e^2iz = 1

e^2iz = e^n2pi Ű 2iz = n2pi

z = np, n = 0,ą1,ą2,ź.

b) Jos w Î C on jakso, niin

sin(z+w) = sinz "z Î C.

Valitaan z = 0:

sinw = sin0 = 0

(12)

Valitaan z = [(p)/2]:

sin

ć
ç
č

ö
÷
ř

sin

= 1

sin

ć
ç
č

ö
÷
ř

cos

ć
ç
č

-w-

ö
÷
ř

cos(-w) = cosw.

Siis cosw = 1.

(13)

(12) Ţ w = np, n = 0,ą1,ą2,ź
(13) Ţ n = 0,ą2,ą4,ź.

4.4 Kuvaus z Ž cosz

Funktioilla e^z ja e^-z on jaksovyönä

ě
í
î

ę
ę

-p < Im z Ł p

ü
ý
ţ

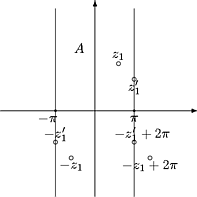
Näin ollen cosz saa joukossa A = { z | -p < Re z Ł p} kaikki mahdolliset arvonsa. Tutkitaan, miten cosz kuvaa joukon A.

Tarkastellaan yhtälöä

cosz = w.

(14)

Sijoitetaan e^iz = t:

e^iz+e^-iz

t²+1

= w

t²-2tw+1 = 0

t²-2tw+w² = w²-1

(t-w)² = w²-1

a) w = ą1

(t-ą1)² = 0 Ű

ě
í
î

t = 1

t = -1

ě
í
î

z = 0

z = p

b) w š ą1

t = ą

____
Öw²-1

Neliöjuuren kaksi eri haaraa antavat kaksi eri t:n arvoa t₁ š 0 ja t₂ š 0.

Yhtälöllä (14) on vastaavasti juuret z₁ Î A ja z₂ Î A, joille e^iz₁ = t₁ ja e^iz₂ = t₂. Koska t₁t₂ = w²-(w²-1) = 1, on e^i(z₁+z₂) = 1 ja z₁+z₂ = n2pŰ z₂ = -z₁+n2p. Yleensä on n = 0, jolloin z₂ = -z₁ Î A. Jos Re z₁ = p, niin z₂ = -z₁+2p Î A. Funktio cosz saa siis kaikki arvot w š ą1 täsmälleen kaksi kertaa joukossa A. Arvot w = 1 ja w = -1 kosini saa pisteissä z = 0 ja z = p.

Kuva 46:

Koska

cosz

cos(x+iy) = cosxcosiy-sinxsiniy

cosxcoshy-isinxsinhy,

on cosz reaalinen suorilla y = 0 ja x = np. Tästä seuraa

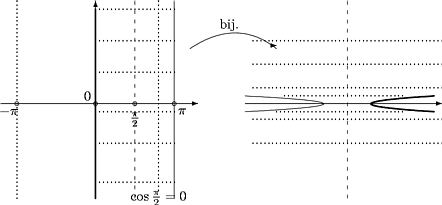Kuva 47:

Esimerkki. Ratkaise yhtälöt
a) sinz = 1
b) cosz = 2i
c) sinz = 100

sinz =

(e^iz-e^-iz ) = 1

e^iz-e^-iz = 2i

(e^iz )²-2ie^iz-1 = 0

e^iz = ią

____
Ö-1+1

= i = e^i[(p)/2]

iz = i

+n2pi

z =

+n2p

cosz =

( e^iz+e^-iz ) = 2i

e^iz+e^-iz-4i = 0

( e^iz )²-4ie^iz+1 = 0

e^iz = 2ią

____
Ö-4-1

= 2iąiÖ5

ě
í
î

e^iz = (2+Ö5)i

e^iz = (Ö5-2)(-i)

ě
í
î

e^-ye^ix = (2+Ö5)e^i[(p)/2]

e^-ye^ix = (Ö5-2)e^-i[(p)/2]

ě
ď
ď
ď
ď
ď
ď
ď
ď
í
ď
ď
ď
ď
ď
ď
ď
ď
î

ě
ď
ď
í
ď
ď
î

x₁ =

+n2p

y₁ = -ln(Ö5+2)

ě
ď
ď
í
ď
ď
î

x₂ = -

+n2p

y₂ = -ln(Ö5-2)

sinz =

(e^iz-e^-iz ) = 100

(e^iz)²-200i e^iz-1 = 0

e^iz = 100ią

________
Ö-10000+1

= i(100ą

____
Ö9999

)

e^-ye^ix = (100ą

____
Ö9999

)e^ip

ě
ď
í
ď
î

x = p+n2p

y = -ln(100ą

____
Ö9999

)

Mitä on sini ja cosi?

sinz

(e^iz-e^-iz)

sini

(e^-1-e¹) = -i

-e

= i

e²-1

Toinen tapa:

siniy

isinhy

sini

isinh1 = i

(e¹-e^-1)

Vastaavasti

cosiy

coshy

cosi

cosh1 =

ć
ç
č

ö
÷
ř