Sisältö

7  Käyräintegraalit

Figure 1: Pinta-ala

Kuvan 1 väritetyn alueen pinta-ala on ò_a^b f(x) dx.

Olkoon j: [ a, b ] ® R² (tai Rⁿ) jatkuva. Joukko j([ a, b ]) Ì R² on käyrä, jota merkitään esimerkiksi G. Kuvaus j on G:n parametriesitys.

Jos käyrällä on parametriesitys, joka on injektio, sitä sanotaan kaareksi. Valitsemalla toinen päätepiste alkupisteeksi ja toinen loppupisteeksi, saadaan suunnistettu kaari. Kaari on säännöllinen, jos sillä on jatkuvasti derivoituva parametriesitys.

Määritelmä 7.1Olkoon G Ì R² säännöllinen suunnistettu kaari ja olkoon j = (j₁, j₂) jatkuvasti derivoituva parametriesitys (siis G = j([ a, b ])). Jos f: G® R ja g: G® R ovat jatkuvia, niin määritellään

ó õ G f dx + g dy : =  b ó õ a æ è f(j(t)) j1¢(t) +g(j(t)) j2¢(t)  ö ø  dt.

Yleisesti:

G Ì Rn,     g: [ a, b ] ® Rn,    g([ a, b ]) = G,     g = (g1, ¼, gn)

jatkuvasti derivoituva. Olkoon f_j : G® R, j = 1, 2, ¼, n. Määritellään

ó õ G f1 dx1 + f2 dx2 + ¼+ fn dxn: =  b ó õ a æ è f1(g(t))g1¢+ ¼+ fn(g(t))gn¢(t)  ö ø  dt

Merkitään myös

ó õ G f1 dx1 + f2 dx2 + ¼+ fn dxn: =  ó õ G f   ·d r   ,

missä [`]f : = (f<sub>1</sub>, ¼, f<sub>n</sub>) ja d[`(r)] : = (dx₁, ¼, dx_n).

Lause Määritelmän 7.1 (sivu pageref) käyräintegraali ei riipu G:n parametriesityksestä.

Todistus.  Sivuutetaan.     ^[¯]

Esimerkki 1 Laske

ó õ G x2 dx + xy dy,

kun G on yksikköympyrän kaari pisteestä (1, 0) pisteeseen (0, 1).

Ratkaisu. Käytetään G:lle tuttua parametrisointia

ì í î x = j1(t) = cost y = j2(t) = sint ,    0 £ t £  p 2 .

Tällöin

j1¢(t)  = -sint, j2¢(t)  = cost dx = j1¢(t) dt,  dy = j2¢(t) dt

ja

ó õ G x2 dx + xy dy =  p/2 ó õ 0 æ è cos2 t ·(-sint) + cost sint cost ö ø  dt = 0.

Toinen mahdollisuus on käyttää G:lle parametriesitystä

ì ï í ï î x = -t y = Ö   1 - t2   ,     t Î [ -1, 0 ].

Tällöin j: [ -1, 0 ] ® R² ja

j(t) =  æ è j1(t), j2(t)  ö ø = (-t,  Ö   1 - t2   ).

Huomaa, että

Ö   x(t)2 + y(t)2   =  Ö   t2 + (1 - t2)   = 1.

Tällä parametriesityksellä

ó õ G x2 dx + xy dy =  0 ó õ -1 æ ç è t2 ·(-1) + (-t)  Ö   1 - t2   ·  -t Ö 1 - t2 ö ÷ ø dt =  0 ó õ -1 (-t2 + t2) dt = 0,

sillä j₁¢(t) = -1 ja

j2¢(t) =   1 2 (1 - t)-[ 1/2] ·(-2t) =   -t Ö 1 - t2

Käyräintegraalin käsite liittyy läheisesti fysiikkaan.

Esimerkki Tarkastellaan massapistettä, joka liikkuu pitkin R³:n käyrää G. Kappaleeseen vaikuttaa voima

F   (x, y, z) = F1(x, y, z) i   + F2(x, y, z) j   + F3(x, y, z) k

missä [`(F)] : R<sup>3</sup> ® R<sup>3</sup>, [`(F)] = (F₁, F₂, F₃).

Massapisteen sijainti ajan t funktiona (aikaväli on a £ t £ b) on

r   (t) = (x(t), y(t), z(t)) = x(t) i   + y(t) j   + z(t) k   ,

katso kuva 2.

Figure 2: Massapisteen sijainti

Kun aika muuttuu (vähän) hetkestä t hetkeen t + Dt, massapisteen paikan muutos on

D r   = r   (t + Dt) - r   (t) =  æ è x(t + Dt) - x(t), y(t + Dt) - y(t), z(t + Dt) - z(t)  ö ø @ æ è x¢(t) Dt, y¢(t) Dt, x¢(t) Dt ö ø = Dt r¢(t).

Tällä välillä tehty työ on

DW @ F   ( r   (t)) ·D r   =  F   ( r   (t)) ·r¢(t) Dt.

Halutaan laskea työ, joka tehdään, kun massapiste siirtyy pisteestä A pisteeseen B. Jaetaan aikaväli [ a, b ] osaväleihin [ t_{k - 1}, t_k ], k = 1, ¼, n. Työksi osavälillä [ t_{k - 1}, t_k ] saadaan

DW @ F   ( r   (tk - 1)) ·r¢(tk - 1)(tk - tk - 1).

Koko työ on

DW @ n å k = 1 F   ( r   (tk - 1)) ·r¢(tk - 1)(tk - tk - 1)

joka suppenee aikajaon tihentyessä kohti integraalia

b ó õ a F   ( r   (t)) · r   ¢(t) dt.

Tässä

b ó õ a F   ( r   (t)) · r   ¢(t) dt = b ó õ a æ è F1(r(t))r1¢(t) + F2(r(t))r2¢(t) + F3(r(t))r3¢(t)  ö ø  dt = ó õ G F1 dx + F2 dy + F3 dz,

eli tehty työ on edellämainitun käyräintegraalin arvo.

Käyräintegraalit voidaan määritellä helposti myös yleisemmille integroimisteille. Olkoot G_i ja G_k suunnistettuja säännöllisiä kaaria siten, että G_i:n loppupiste on G_{i + 1}:n alkupiste. Silloin G_i:t muodostavat paloittain säännöllisen tien G. (G = È_{i = 1}^k G_i.) Määritellään

ó õ G f1 dx1 + ¼+ fn dxn: =  n å i = 1 ó õ Gi f1 dx1 + ¼+ fn dxn.

Esimerkki Tutkitaan integraalia

ó õ G y dx - x dy + dz.

a) G on jana jonka alkupiste on (1, 0, 0) ja loppupiste (0, 1, 1). G:n parametrisointi:

j(t) = (1 - t)(1, 0, 0) + t(0, 1, 1) = (1 - t, t , t) = : (j1, j2, j3),     t Î [ 0, 1 ].

Nyt

j1¢(t) = -1,     j2¢(t) = 1 = j3¢(t)

joten

ó õ G y dx - x dy + dz = 1 ó õ 0 æ è j2(t) j1¢(t) - j1(t) j2¢(t) + j3¢(t)  ö ø  dt = 1 ó õ 0 æ è t ·(-1) - (1 - t) ·1 + 1  ö ø  dt = t ó õ 0 -t - 1 + t + 1 dt = 0.

b) G on ruuviviiva

G =  ì í î (cost, sint,   2 p t)  ê ê  t Î é ë 0,   p 2 ù û ü ý þ ,

Nyt

j1(t)  = cost,  j2(t)  = sint,  j3(t)  =  2 p t j1¢(t)  = -sint,  j2¢(t)  = cost,  j3¢(t)  =  2 p

joten

ó õ G y dx - x dy + dz = p/2 ó õ 0 æ è j2(t) j1¢(t) + j1(t) j2¢(t) + j3¢(t)  ö ø  dt = p/2 ó õ 0 æ è -sin2 t - cos2 t +   2 p ö ø  dt = p/2 ó õ 0 (-1+   2 p ) dt = -  2 p + 1 ¹ 0.

7.1  Vektorikentän potentiaali

Määritelmä 7.2Olkoon A Ì °  R² alue ja f : A ® R², f = (f₁, f₂) vektorikenttä. Jos on olemassa differioituva funktio u : A ® R (skalaariarvoinen!) siten, että Ñu = f (eli f₁ = D₁u, f₂ = D₂u) niin u on funktion f potentiaali. Sanotaan myös, että lauseke

f1 dx1 + f2 dx2

on eksakti ja u on sen integraalifunktio.

Huomautus 1 Kaikilla vektorikentillä ei ole olemassa potentiaalia.

Huomautus 2 Potentiaali on yksikäsitteinen lisättävää vakiota vaille: Jos u on funktion f potentiaali, niin v : A ® R on funktion f potentiaali jos ja vain jos on olemassa vakio c Î R siten, että v = u + c.

Esimerkki 1 Olkoon

f(x, y) = (3x2y + cos(x + y), x3 + cos(x + y)),     f : R2 ® R2.

Tällöin

u(x, y) = x3y + sin(x + y),

ja pätee Ñu = f.

Esimerkki 2 Olkoon

f(x, y) = (10x2, cosx + ey).

Tällä ei ole potentiaalifunktiota. Tähän tapaukseen palaamme myöhemmin.

Edellä oleva Määritelmä 7.2 (sivu pageref) toimii myös avaruudessa Rⁿ: Olkoon f : A ® Rⁿ, missä A Ì Rⁿ on alue. Tällöin u : A ® R on funktion f potentiaali, jos Ñu = f.

Esimerkki Olkoon

f(x, y, z) =  æ è  x r3 ,   y r3 ,   z r3 ö ø ,    f : R3 \{ 0   } ® R3,

missä

r   = (x, y, z) = x i   + y j   + z k   ,  r = ê ê   r     ê ê =  Ö   x2 + y2 + z2   .

Voidaan kirjoittaa f(x, y, z) = [([`(r)])/(r³)]. Tällä on potentiaali u(x, y, z) = -[ 1/(r)], sillä

D1 u =   ¶ ¶x (-(x2 + y2 + z2)-[ 1/2]) =   1 2 (x2 + y2 + z2)-[ 3/2] ·2x =   x r3 = f1jne.

Lause 7.3Olkoon f : A ® Rⁿ jatkuva vektorikenttä, A Ì °  Rⁿ alue ja f = (f₁, ¼, f_n). Olkoon u : A ® R funktion f potentiaali. Jos [`(a)] = (a<sub>1</sub>, ¼, a<sub>n</sub>) Î A, [`(b)] = (b₁, ¼, b_n) Î A ja G Ì A paloittain säännöllinen tie alkupisteenä [`(a)] ja loppupisteenä [`(b)], niin

ó õ G f1 dx1 + ¼+ fn dxn = u( b   ) - u( a   ).

Katso kuva 3.

Figure 3: Kaari G

Todistus.  Oletetaan aluksi, että G on säännöllinen kaari, toisin sanoen, on olemassa jatkuvasti derivoituva parametriesitys

j = (j1, ¼, jn),     j: [ a, b] ® Rn.

Ketjusäännöstä seuraa, että

(u °j)¢(t) =  n å i = 1 (Di u)(j(t)) ji¢(t) =  n å i = 1 fi (j(t)) ji¢(t),    t Î [ a, b] Ì R.

Käyräintegraalin määritelmästä seuraa

ó õ G f1 dx1 + ¼+ fn dxn = b ó õ a [ f1(j(t))j1¢(t) + ¼+ fn(j(t))jn¢(t) ] dt = b ó õ a (u °j)¢(t) dt = [ u °j]t = ab = u(j(b)) - u(j(a)) = u( b   ) - u( a   ).

    ^[¯]

Jos G on säännöllinen tie, jaetaan tarkastelu säännöllisiin osakaariin.

Esimerkki Laske

ó õ G yz dx + xz dy + xy dz (*) ,

kun G on ruuviviiva,

ì ï í ï î x = cost y = sint z = t ,    t Î [ 0, 2p].

Alkupiste on (1, 0, 0) ja loppupiste (1, 0, 2p),

Ratkaisu. Määritellään u(x, y, z) = xyz. Tällöin

Ñu(x, y, z) = (yz, xz, xy).

Siten (*) on eksakti funktio ja Lauseen 7.3 (sivu pageref) nojalla

ó õ G yz dx + xz dy + xy dz = u(1, 0, 2p) - u(1, 0, 0) = 1 ·0 ·2p- 1 ·0 ·0 = 0.

Lause 7.4Olkoon A Ì °  R² ympyrä (kiekko), f : A ® R² jatkuvasti derivoituva ja f = (f₁, f₂). Tällöin funktiolla f on potentiaali jos ja vain jos

D1 f2 = D2 f1(integroituvuusehto).

Huomautus Lause 7.4 (sivu pageref) ei päde kaikilla alueille A; se voidaan kyllä yleistää niin sanotuille yhdesti yhtenäisille alueille. Katso kuva 4.

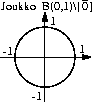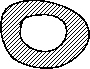Yhdesti yhtenäinen  Yhtenäisiä, mutta eivät yhdesti yhtenäisiä

Lauseen 7.4 (sivu pageref) todistus. Väite: Funktiolla f on potentiaali jos ja vain jos D₂ f₁ = D₁ f₂.

Todistus.  1. Oletetaan, että funktiolla f on potentiaali u, eli

ì í î D1 u = f1 D2 u = f2 .

Derivointijärjestys on vaihdannainen, joten

D1 (D2 u)  = D2 (D1 u)  Þ D1 f2 = D2 f1.

2. Oletetaan, että D₂ f₁ = D₁ f₂. Merkitään pisteellä (a, b) alueen A keskipistettä. Olkoon nyt (x, y) Î A mielivaltainen piste. Määritellään

u(x, y) : =  y ó õ b f2 (a1, x2)  dx2 +  x ó õ a f1(x1, y)  dx1 æ è =  ó õ G f1  dx1 + f2  dx2 ö ø .

Lasketaan

D1 u(x, y) =    D1 y ó õ b f2(a, x2)  dx2 = 0     + D1 x ó õ a f1(x1, y)  dx1 = f1(x, y),

ja

D2 u(x, y)  = D2 y ó õ b f2(a, x2)  dx2 + D2 x ó õ a f1(x1, y)  dx1 = f2(a, y) +  x ó õ a D2 f1(x1, y)  dx1 = f2(a, y) +  x ó õ a D1 f2(x1, y)  dx1 = f2(a, y) + [ f2(x1, y) ]x1 = ax = f2(a, y) + f2(x, y) - f2(a, y)  = f2(x, y).

Perustelu sille, että tässä voidaan derivoida integraalimerkin alla, sivuutetaan.     ^[¯]

Esimerkki Laske

ó õ G  2x(1 - ey) (1 + x2)2  dx +   ey 1 + x2  dy,

kun

G =  ì í î (x, y)  ê ê  x = cost, y = sint, t Î é ë 0,   p 2 ù û ü ý þ .

Tien alkupiste on (1, 0) ja loppupiste (0, 1). Merkitään

f1(x, y)  =  2x(1 - ey) (1 + x2)2 f2(x, y)  =  ey 1 + x2

Tällöin

D2 f1(x, y)  = D2 é ë  2x (1 + x2)2 -  2xey (1 + x2)2 ù û = -  2x (1 + x2)2 ey D1 f2(x, y)  = D1  ey 1 + x2 = -  ey ·2x (1 + x2)2 ,

eli D₂ f₁ = D₁ f₂. (Yhtälö D₂ f₁ = D₁ f₂ pätee koko tasossa R², esimerkiksi joukossa B(0, 10⁶).) Siten vektorikentällä f : = (f₁, f₂) on potentiaali u ja Lauseen 7.3 (sivu pageref) mukaan

u(0, 1) - u(1, 0) =  ó õ G f1 dx + f2 dy.

Tämä voidaan tulkita myös niin, että integraalin arvo ei riipu integroimistiestä. Valitsemme uuden integroimistien [(G)\tilde] siten, että kuljetaan pisteestä (0, 1) pisteeseen (1, 0) koordinaattiakselien suuntaisia janoja pitkin origon kautta. Lasketaan

ó õ [(G)\tilde] f1 dx + f2 dy =  ó õ G1 f1 dx + f2 dy +  ó õ G2 f1 dx + f2 dy

Tässä G₁ : j(t) = (1 - t, 0), t Î [ 0, 1 ] ja j₁¢ = -1, j₂¢ = 0, joten

ó õ G1 f2 dy = 0 ja   f1(x, 0) =   2x(1 - e0) (1 + x2)2 = 0.

Siten

ó õ G1 = 0.

G₂:n parametriesitys: j(t) = (0, t), t Î [ 0, 1 ] ja j₁¢ = 0, j₂¢ = 1.

ó õ G2 ¼ =  1 ó õ 0  et 1 + 0 j2¢(t) dt =  1 ó õ 0 et dt = e - 1.

Vastaus on siis -1.

Esimerkki Lause 7.4 (sivu pageref) ei päde kaikille alueille A!

Olkoon

f(x, y) =  æ è  -y x2 + y2 ,   x x2 + y2 ö ø ,    f: A ® R2,  A = R2 \{0, 0}.

Edelleen

D2 f1 =  -(x2 + y2) + 2y2 (x2 + y2)2 =   y2 - x2 (x2 + y2)2 D1 f2 =  x2 + y2 - 2x2 (x2 + y2)2 =   y2 - x2 (x2 + y2)2

siten D₂ f₁ = D₁ f₂ joukossa A. Tarkastellaan integraalia

ó õ f1 dx + f2 dy,

kun

G = { (x, y)  ê ê  x = cost, y = sint; t Î [ 0, 2p] }

(eli G on yksikköympyrän reuna).

Jos funktiolla f on potentiaali u koko tasossa R², niin Lauseen 7.3 (sivu pageref) nojalla

ó õ f1 dx + f2 dy = u( b   ) - u( a   ) = 0,

koska G:n loppupiste [`(b)] ja G:n alkupiste [`(a)] ovat sama (1, 0).

Lasketaan käyräintegraali suoraan:

j(t) = (cost, sint),     j1¢ = -sint, j2¢ = cost.

Näin ollen

ó õ G f1 dx + f2 dy = 2p ó õ 0 é ë  -sint 1 (-sint) +   cost 1 ·cost ù û  dt = 2p ó õ 0 [ sin2 t + cos2 t ] dt = 2p ó õ 0 1 dt = 2p ¹ 0.

Lause 7.4 (sivu pageref) ei näin ollen voi päteä.

Huomautus Jos G on suljettu (umpinainen) integroimistie (alku- ja loppupiste samat), niin

ó õ G f1 dx + f2 dy

(f kuten edellä) on "2p kertaa G:n kierrosluku nollan suhteen".

Lause 7.5 Olkoon A ympyrä, f: A ® R jatkuva. Funktiolla f on potentiaali u : A ® R, jos ja vain jos

ó õ G f1 dx + f2 dy = 0, (pyörteettömyys)

kun G on mielivaltainen umpinainen paloittain säännöllinen tie.

Potentiaalin laskeminen

Jos esimerkiksi valitaan G:ksi murtoviiva (a, b) ® (a, y) ® (x, y) sekä u(a, b) = 0, saadaan u:n arvo pisteessä (x, y) kaavasta

u(x, y) =  y ó õ b f2(a, x2) dx2 +  x ó õ a f1(x1,y) dx1.

Vaihtoehtoisesti, jos G on murtoviiva (a, b) ® (x, b) ® (x, y), saadaan

u(x, y) =  x ó õ a f1(x1, b) dx1 +  y ó õ b f2(x, x2) dx2.

Katso kuva 5.

Figure 5: Murtoviiva

Esimerkki Laske vektorikentän

f : = (5x4y4, 4x5y3 + 1)

potentiaali.

Ratkaisu. 1) Tarkastellaan, onko potentiaalia: Pätee

D1 f2(x, y) = 20x4 y3 = D2 f1(x, y),     "(x, y) Î R2,

joten potentiaali u on olemassa koko tasossa.

2) Valitaan u(0, 0) = 0 ja G: (0, 0) ® (x, 0) ® (x, y). Saadaan

u(x, y)  = x ó õ 0 f1(x1, 0) dx1 +  y ó õ 0 f2(x, x2) dx2 = x ó õ 0 5x14 ·0 dx1 +  y ó õ 0 (4x5 x23 + 1) dx2 = 0 + [ x5 x24 + x2 ]x2 = 0y = x5 y4 + y.

Tarkistus:

Ñu(x, y) = (5x4 y4, 4x5 y3 + 1).

Potentiaalin laskeminen avaruudessa Rⁿ

Lauseen 7.4 (sivu pageref) integroituvuusehto avaruudessa Rⁿ:

Di fj = Dj fi,      " i, j = 1, ¼, n,     i ¹ j.

Esimerkki Olkoon

f(x, y, z) =  æ è y - sin(x + z), x, -sin(x + z)  ö ø .

Integroituvuus ehdot

D1 f2 = 1 = D2 f1 D1 f3 = -cos(x + z) = D3 f1 D2 f3 = 0 = D3 f2

toteutuvat, joten

u(x, y, z) = xy + cos(x + z).

Tapauksessa n = 3 merkitään

Ñ×f :=   ê ê ê ê ê ê i   j   k   D1 D2 D3 f1 f2 f3 ê ê ê ê ê ê   =  i     ê ê ê D2 D3 f2 f3 ê ê ê  + j     ê ê ê D1 D3 f1 f3 ê ê ê  + k     ê ê ê D1 D2 f1 f2 ê ê ê   = (D2 f3 - D3 f2) i   + (D1 f3 - D3 f1) j   + (D1 f2 - D2 f1) k   .

Integroituvuusehto pätee jos ja vain jos Ñ×f = [`0] alueessa A.

Sanomme, että vektorikenttä f on pyörteetön, jos

ó õ G f1 dx1 + ¼+ fn dxn = 0

jokaiselle umpinaiselle G.

7.2  Integrointi kaaren pituuden suhteen

Figure 6: Kaaren pituus

Väliä [ a, t ] vastaava kaaren pituus

s = l(t) =  t ó õ a Ö   j1¢(t)2 + j2¢(t)2    dt.

Funktio on l: [ a, b ] ® [ 0, L ] jatkuvasti derivoituva bijektio, koska

l¢(t) =  Ö   j1¢(t)2 + j2¢(t)2   > 0.

l(t) on kaaren pituus pisteestä j(a) pisteeseen j(t) ja l on aidosti kasvava.

Määritellään y: = (y₁, y₂) : [ 0, L ] ® R², y(s) = j°l^-1(s). Funktion y on mittatarkka parametrisaatio polulle G, katso kuva 7.

Figure 7: Parametrisaatio polulle G

ì í î x = j1(t)  = j1(l-1(s))  = y1(s)  y = j2(t)  = j2(l-1(s))  = y2(s) ,     0 £ s £ L.

Olkoon f : G® R jatkuva. Määritellään funktion f integraali kaaren pituuden suhteen

ó õ G f ds : =  L ó õ 0 f(y(s)) ds.

Laskujen helpottamiseksi suoritetaan muuttujan vaihto:

s = l(t) =  t ó õ a Ö   j1¢(t)2 + j2¢(t)2    dt,   ds dt =  d dt t ó õ 0 Ö   j1¢(t)2 + j2¢(t)2   : =  Ö   j1¢(t)2 + j2¢(t)2   .

Saadaan

ó õ G f ds =  L ó õ 0 f(y(s)) ds =  b ó õ a f(j(t))  Ö   j1¢(t)2 + j2¢(t)2    dt.

Integraalin geometrinen tulkinta: se on funktion f kuvaajan ja x-y-tasossa olevan käyrän G väliin jäävän liuskan pinta-ala. Katso kuva 8.

Figure 8:

Avaruudessa R³:

ó õ G f ds =  b ó õ a f(y(s)) ds =  b ó õ a f(j(t))  Ö   j1¢(t)2 + ¼+ jn¢(t)2    dt,

missä j: [ a, b ] ® Rⁿ, on G:n parametriesitys.

Esimerkki (Katso kuva 9.)

Figure 9:

Jos kaarella G on massa, jonka tiheys r(x, y), niin painopisteen koordinaatit ovat:

X = ó õ G xr(x, y),ds ó õ G r(x, y) ds , Y = ó õ G yr(x, y),ds ó õ G r(x, y) ds .

Esimerkki Oletetaan, että r on vakio=:r ja G on puoliympyrä

{ (x, y)  ê ê  x2 + y2 = 1, y ³ 0 }.

Reunalla G on parametriesitys

ì í î x = cost = : j1(t)  y = sint = : j2(t) ,     t Î [ 0, p].

Lasketaan

ó õ G r(x, y) ds =  p ó õ 0 r0 Ö   sin2(t) + cos2(t)    dt = r0p

ja

ó õ G xr(x, y) ds = p ó õ 0 r0 j1(t)  Ö   j1¢(t)2 + j2¢(t)2    dt =  p ó õ 0 r0 cost dt = 0  ó õ G yr(x, y) ds = p ó õ 0 r0 sint dt = 2r0

eli

X =   0 pr0 = 0,     Y =   2r0 pr0 =   2 p .