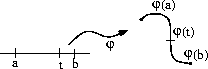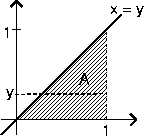\LARGE{Analyysi II}

Analyysi II

Jari Taskinen

Sep 27, 2002

Sisältö

1  Vektoriavaruudet \@mathbf R2, \@mathbf R3, \@mathbf R4
    1.1  Geometrinen havainnollistus
    1.2  Tason topologiaa
2  Useamman muuttujan funktiot
3  Differentiaalilaskenta
    3.1  Osittaisderivaatta
    3.2  Korkeamman kertaluvun derivaatat
    3.3  Differentioituvuus
    3.4  Gradientti ja suunnatut derivaatat
    3.5  Yhdistettyjen kuvausten derivoiminen
4  Käyrät, tasa-arvopinnat ja tangenttitaso
    4.1  Pinnat
    4.2  Tangenttitasot
5  Väliarvolause
    5.1  Implisiittifunktiolause
6  Ääriarvojen teoriaa
    6.1  Taylorin kaava
    6.2  Ääriarvoista
7  Käyräintegraalit
    7.1  Vektorikentän potentiaali
    7.2  Integrointi kaaren pituuden suhteen
8  Pintaintegraalit
    8.1  Muuttujien vaihto pintaintegraaleissa
    8.2  Käyrä- ja pintaintegraalien yhteys
    8.3  Integrointi yli pinnan
9  Avaruusintegraalit
    9.1  Muuttujan vaihto avaruusintegraalissa
    9.2  Pinta-ja avaruusintegraalien välinen yhteys

1  Vektoriavaruudet R2, R3, R4

Merkitään
R2
: =
ì
í
î 		(x, y)   ê
ê 		 x Î R, y Î R ü
ý
þ
R3
: =
ì
í
î 		(x, y, z)   ê
ê 		 x, y, z Î R ü
ý
þ
Rn
: =
ì
í
î 		(x1, ¼, xn)   ê
ê 		 xj Î R,  " j = 1, ¼, n ü
ý
þ 		(tässä n Î N)
Näiden joukkojen alkioita sanotaan pisteiksi tai vektoreiksi ja niitä merkitään esimerkiksi
x
 
=
(x1, x2) Î R2
y
 
=
(y1, y2, y3) Î R3
a
 
=
(a1, a2, a3, a4) Î R4
Lukua x1 sanotaan pisteen [`(x)]:n 1. komponentiksi/koordinaatiksi, lukua x2 pisteen [`(x)]:n 2. komponentiksi/koordinaatiksi, jne. Nollavektori on [`0] = (0, 0) Î R2, [`0] = (0, 0, 0) Î R3¼ sitä sanotaan myös origoksi.

Tarkastellaan avaruutta R2. Vektorien [`(x)] = (x1, x2) ja [`(y)] = (y1, y2) yhteenlasku määritellään kaavalla
x
 
 +
y
 
 = (x1 + y1, x2 + y2).

Esimerkki 1
(1, 10) + (3, p) + (-4, 0) = (1 + 3 + (-4), 10 + p+ 0) = (0, 10 + p).

Vektorin [`(x)] = (x1, x2) kertominen reaaliluvulla a määritellään
a
x
 
 = (ax1, ax2).

Esimerkki 2
5(e, e2) = (5e, 5e2).

Vektorien [`(x)] ja [`(y)] erotus määritellään
x
 
 -
y
 
 =
x
 
 + (-
y
 
 ),
missä -[`(y)] = -1 ·(y1, y2) = (-y1, -y2).

Merkitään [`(e)]1 = (1, 0), [`(e)]2 = (0, 1) (kantavektorit). Jos vektori [`(x)] = (x1, x2) Î R2, niin se voidaan kirjoittaa muodossa
x
 
 = x1
e
 
1 
 + x2
e
 
2 
tai
e
 
1 
 =
i
 
     ja    
e
 
2 
 =
j
 
 .
Siis myös
x
 
 = x1
i
 
 + x2
j
 
 .

Jos n Î N, niin määritelmät ovat analogisia. Olkoon a Î R ja
x
 
=
(x1, x2, ¼, xn) Î Rn
y
 
=
(y1, y2, ¼, yn) Î Rn.
Määritellään
x
 
 +
y
 
:=
(x1 + y1, x2 + y2, ¼, xn + yn) Î Rn,
a
x
 
:=
(ax1, ax2, ¼,axn) Î Rn,
-
x
 
:=
(-x1, -x2, ¼, -xn) Î Rn
ja kantavektorit
e
 
1 
=
(1, 0, 0, ¼, 0),
e
 
2 
=
(0, 1, 0, ¼, 0),
:
e
 
n 
=
(0, 0, 0, ¼, 1).

Jos [`(x)] = (x1, ¼, xn), niin
x
 
 = x1
e
 
1 
 + ¼+ xn
e
 
n 
 = n
å
j = 1 
 xj
e
 
j 
 .
Olkoon [`(x)] = (x1, ¼, xn) Î Rn, [`(y)] = (y1, ¼, yn) Î Rn. Niiden sisätulo (skalaari-, pistetulo) määritellään
x
 
 ·
y
 
 : = x1 y1 + x2 y2 + ¼+ xn yn Î R.

Esimerkki 3 Tapauksessa n = 4, lasketaan sisätulo
(1, 0, -2,  1
2
 ) ·(1, 0, 1, 0) = 1 ·1 + 0 ·0 + (-2) ·1 +  1
2
 ·0 = -1.

Lause 4 Jos [`(x)],[`(y)] Î Rn ja a, b Î R, niin

Esimerkki 5 Jos n = 3, [`(x)] = (1, 1, 0), [`(y)] = (0, 3, -1), [`(z)] = (0, 1, 2), a = 1 ja b = 2, niin
x
 
 ·(a
y
 
 + b
z
 
 ) = (1, 1, 0) ·[ (0, 3, -1) + (0, 2, 4) ] = (1, 1, 0) ·(0, 5, 3) = 5.
Toisaalta
a
x
 
 ·
y
 
 + b
x
 
 ·
z
 
 = (1, 1, 0) ·(0, 3, -1) + 2(1, 1, 0) ·(0, 1, 2) = 3 + 2 = 5.

Vektorin [`(x)] Î Rn pituus eli normi määritellään
ê
ê 		 
x
 
   ê
ê 		=   æ
Ö
x
 
 ·
x
 
 
 =
Ö
 
x12 + x22 + ¼xn2
 
 .

Lause 6

Merkitään vielä
d(
x
 
 ,
y
 
 ) : = ê
ê 		 
x
 
 -
y
 
   ê
ê 		=
Ö
 
(x1 - y1)2 + ¼+ (xn - yn)2)
 
(pisteiden [`(x)] ja [`(y)] etäisyys).

Jos [`(x)],[`(y)] Î Rn ja [`(x)] ·[`(y)] = 0, niin sanotaan, että [`(x)] ja [`(y)] ovat kohtisuorassa toisiaan vastaan, merkitään [`(x)] ^[`(y)].

1.1  Geometrinen havainnollistus

Taso R2: Katso kuvat 1 ja 2. Avaruus R3: Katso kuva 3.

GeomHav1.png
Figure 1: Taso R2

GeomHav2.png
Figure 2: Taso R2

GeomHav3.png
Figure 3: Avaruus R3

1.2  Tason topologiaa

Määritelmä 1 Olkoon ([`(x)]k)k = 1¥ jono vektoreita R2:ssa. Jono suppenee kohti pistettä [`(x)] Î R2, jos

lim
k ® ¥ 
 ê
ê 		 
x
 
k 
 -
x
 
   ê
ê 		= 0
(1)
Tällöin merkitään

lim
k ® ¥ 
x
 
k 
 =
x
 
 .

Ehto (1) tarkoittaa: Kaikilla r > 0 voidaan löytää luku N Î N seuraavasti:
ê
ê 		 
x
 
k 
 -
x
 
   ê
ê 		< r, jos k > N.

Esimerkki 2 Olkoon
x
 
k 
 = æ
è 		2 +  1
k
 ,  k - 3
k
 ö
ø 		,     k Î N.
Suppeneeko jono
(
x
 
k 
 )k=1¥ Ì R2?

Ratkaisu.
x
 
1 
=
( 2 +  1
1
 ,  1 - 3
1
 ) = ( 3, -2 )     ( ¹ x1)
x
 
2 
=
( 2 +  1
2
 ,  2 - 3
2
 ) = ( 2  1
2
 , -  1
2
 )
x
 
3 
=
( 2  1
3
 , 0 )
x
 
4 
=
( 2  1
4
 ,  1
4
 )
x
 
5 
=
( 2  1
5
 ,  2
5
 )
:
Väite:

lim
k ® ¥ 
x
 
k 
 = (2, 1) = :
x
 

Todistus. 
ê
ê 		 
x
 
k 
 -
x
 
   ê
ê
=
ê
ê 		 (2 +  1
k
 ,  k - 3
k
 ) - (2, 1)  ê
ê 		= ê
ê 		 (  1
k
 ,  k - 3 - k
k
 )  ê
ê
=
ê
ê 		   1
k
 ,  -3
k
   ê
ê 		= ê
ê 		   1
k
 (1, -3)  ê
ê 		=  1
k
 | (1, -3) | =

Ö
10
k
 .
Tämä lähestyy nollaa, kun k lähestyy ääretöntä.     [¯]

Lause 3 Olkoon ([`(x)]k)k = 1¥ Ì R2 jono vektoreita, xk = (x1k, x2k) ja [`(x)] = (x1, x2) Î R2. Tällöin

lim
k ® ¥ 
x
 
k 
 =
x
 
 Û ì
ï
ï
í
ï
ï
î

lim
k ® ¥ 
 x1k
=
x1

lim
k ® ¥ 
 x2k
=
x2.

Esimerkki 4 Olkoon
x
 
k 
 = æ
è 		sin æ
è 		 1
k
 ö
ø 		,cos æ
è 		 1
k
 ö
ø 		ö
ø 		,      " k Î N.
Tässä x1k = sin([ 1/(k)]) ja x2k = cos([ 1/(k)]).

Pätee:

lim
k ® ¥ 
 x1k
=

lim
k ® ¥ 
 sin(  1
k
 ) = 0

lim
k ® ¥ 
 x2k
=

lim
k ® ¥ 
 cos(  1
k
 ) = 1,
joten lauseen 1.2.3 nojalla

lim
k ® ¥ 
x
 
k 
 = (0, 1) Î R2.

Lause 5 Jos limk ® ¥[`(x)]k = [`(x)], limk ® ¥[`(y)]k = [`(y)] ja (ak)k = 1¥ Ì R on sellainen jono, että limk ® ¥ ak = a, niin

Olkoon [`(a)] : = (a1, a2) Î R2, r > 0.

Määritelmä 6 [`(a)]-keskeinen r-säteinen avoin pallo (kiekko) on joukko
B(
a
 
 , r) = ì
í
î
y
 
 Î R  ê
ê 		  ê
ê 		 
y
 
 -
a
 
   ê
ê 		< r ü
ý
þ 		.
Huomaa, että
ê
ê 		 
y
 
 -
a
 
   ê
ê 		=
Ö
 
(y1 - a1)2 + (y2 - a2)2
 
on pisteiden [`(y)] ja [`(a)] etäisyys! Katso kuva 4. Joukkoa B([`(a)], r) sanotaan myös [`(a)]:n (r-säteiseksi) palloympäristöksi.

Vastaavasti määritellään suljettu kiekko
B(
a
 
 , r) : = ì
í
î
y
 
   ê
ê 		  ê
ê 		 
y
 
 -
a
 
   ê
ê 		£ r ü
ý
þ
(sisältää kiekon reunan) ja punkteerattu kiekko
B(
a
 
 , r) : = ì
í
î
y
 
   ê
ê 		 0 < ê
ê 		 
y
 
 -
a
 
   ê
ê 		< r ü
ý
þ 		.
Vielä toistamme, että
y
 
 Î B(
a
 
 , r) Û (y1 - a1)2 + (y2 - a2)2 < r2.

TasTop2.png
Figure 4: B([`(a)], r)

Määritelmä 7 Joukko A Ì R2 on avoin, jos jokaista [`(x)] Î A kohti on olemassa sellainen kiekko B([`(x)], r), että B([`(x)], r) Ì A.

Esimerkki 8 Osoitetaan että joukko
A : = ì
í
î 		(x1, x2) Î R2   ê
ê 		 x1 > 2 ü
ý
þ
on avoin. Katso kuva 5.

TasTop3.png
Figure 5: Avoin joukko

Ratkaisu. Olkoon [`(x)] Î A. Silloin x1 > 2. Valitaan r : = [(x1 - 2)/20]. On osoitettava, että jos [`(y)] Î B([`(x)], r), niin [`(y)] Î A. Pätee
|  y1 - x1  | =
Ö
 
(y1 - x1)2
 
 £
Ö
 
(y1 - x1)2 + (y2 - x2)2
 
 £ r =  x1 - 2
20
 .
Tarkastellaan kahta tapausta 1. Jos y1 ³ x1, niin y1 > 2 (sillä x1 > 2), eli [`(y)] Î A

2. Jos y1 < x1, niin
|  y1 - x1  |
£
 x1 - 2
20
Û
x1 -  x1 - 2
20
£
y1
Û
2 + (x1 - 2) -  x1 - 2
20
£
y1
Û
2 + [1 -  1
20
 ] ·(x1 - 2)
£
y1
Þ
2
<
y1,
eli taas [`(y)] Î A.

Lause 9 Avoin pallo on aina avoin joukko. Avoin suorakulmio
ì
í
î
x
 
 Î R2   ê
ê 		 a < x1 < b, c < x2 < d ü
ý
þ
on avoin joukko.

Tässä a,b,c,d Î R, a < b, c < d. Katso kuva 6.

TasTop4.png
Figure 6: Avoin suorakulmio

Määritelmä 10 Joukko A Ì R2 on suljettu, jos (komplementti) R2 \A on avoin. Katso kuva 7.

TasTop5.png
Figure 7: Suljettu joukko

Jana
ì
í
î 		(x, 0)   ê
ê 		 0 £ x £ 10 ü
ý
þ 		=: A
on suljettu. Merkitään B : = R2 \A. Joukko B sisältää kahdenlaisia pisteitä [`(y)] : = (y1, y2):

Todistetaan, että joukko B on avoin. Olkoon [`(y)] Î B.

Tapaus 1° Valitaan esimerkiksi r = [(|y2|)/2]. Tällöin B([`(y)], r) Ì B.

Tapaus 2° Pätee y1 < 0 Úy1 > 10. Jos y1 < 0, valitaan r = [(|y1|)/2] mistä seuraa B([`(y)], r) Ì B. Jos y1 > 10, valitaan r = [(y1 - 10)/2] mistä seuraa B([`(y)], r) Ì B.

Esimerkki 11 Joukko
A : = ì
í
î 		(x, 0)   ê
ê 		 0 < x < 10 ü
ý
þ
ei ole avoin eikä suljettu.

Selitys. Joukko A ei ole avoin, koska jos valitaan [`(x)] = (5, 0) ja r > 0 mielivaltainen, niin B(x, r) \not Ì A. Joukko A ei ole suljettu koska jos merkitään B = R2 \A, piste (0, 0) Î B. Nyt B ei ole avoin. Olkoon r > 0 mielivaltainen. Joukko B(0, r) sisältää A:n pisteitä B(0, r) \not Ì B joten B ei ole avoin. Näin ollen A ei ole suljettu.

Heuristisesti: Katso kuva 8.

TasTop6.png
Figure 8: Joukot A ja K

Esimerkki 12 Olkoon
A : = ì
í
î 		x = (x1, x2) Î R2   ê
ê 		 0 £ x1 £ 1, 0 < x2 < 1 ü
ý
þ 		.
Joukko A ei ole avoin eikä suljettu. Katso kuva 9.

TasTop7.png
Figure 9: Joukko A

Määritelmä 13 Olkoon A Ì R2, [`(x)] Î R2. Piste [`(x)] on joukon A kasaantumispiste, jos jokainen [`(x)]:n ympäristö sisältää vähintään yhden A:n pisteen [`(y)], [`(y)] ¹ [`(x)].

Esimerkki 14 Olkoon
A : = ì
í
î 		æ
è 		 1
k
 ,  1
k
 ö
ø 		  ê
ê 		 k Î N ü
ý
þ 		.
Piste [`0] on A:n kasaantumispiste. Katso kuva 10.

TasTop8.png
Figure 10: Kasaantumispiste

Lause 15 Jos [`(x)] on A:n kasaantumispiste, niin jokainen B([`(x)], r) sisältää äärettömän monta A:n pistettä. Lisäksi on olemassa jono ([`(x)]k)k = 1¥ Ì A siten, että limk ® ¥[`(x)]k = [`(x)].

Määritelmä 16 Joukon A sulkeuma on joukko
A
 
 : = {
x
 
 Î R2   ê
ê 		 
x
 
 Î A tai
x
 
 on A:n kasaantumispiste }.

Lause 17 Jos A Ì R2, niin [`(A)] on suljettu joukko. Jos B on suljettu joukko, niin [`(B)] = B.

Seuraus 18 A on suljettu, jos ja vain jos A sisältää kaikki kasaantumispisteensä.

Esimerkki 19 Joukko
B : = ì
í
î 		æ
è 		1, 3 +  1
k
 ö
ø 		  ê
ê 		 k Î N ü
ý
þ
ei ole suljettu. Joukko
C : = B È{ (1, 3) }
on suljettu.

Määritelmä 20 Piste [`(x)] on joukon A sisäpiste jos on olemassa ympäristö B([`(x)], r), r > 0 siten, että B([`(x)], r) Ì A.

Piste [`(x)] on joukon A ulkopiste, jos [`(x)] Î R2 \A ja on olemassa s > 0 siten, että B([`(x)], s) Ì R2 \A.

Piste [`(x)] on joukon A reunapiste, jos sen jokainen ympäristö B([`(x)], r), r > 0 sisältää sekä A:n että R2 \A:n pisteitä.

Esimerkki 21 Olkoon joukko
C : = { (x, y)   ê
ê 		 1 < x £ 3, 2 < y £ 4 }
Piste (1 + [ 1/100], 2 + [ 1/1000]) Î C on sisäpiste, (2, 4) Î C ei ole sisäpiste. Piste (3[ 1/2], 3) on joukon C ulkopiste, (2, 2) Î R2 \C ei ole ulkopiste. Pisteet (2, 2) ja (2, 4) ovat joukon C reunapisteitä.

Todistus.  Tapaus (2, 2): Olkoon r > 0 mielivaltainen.

1° Joukko B( (2, 2), r ) sisältää C:n pisteitä: määritellään r¢ = min(1, r) ja [`(b)] = (2, 2 + [(r¢)/2]). Tällöin [`(b)] Î B( (2, 2), r);
ê
ê 		  (2, 2) -
b
 
   ê
ê 		= ê
ê 		  (2, 2) - æ
è 		2, 2 +  r¢
2
 ö
ø 		  ê
ê 		= ê
ê 		  æ
è 		0,  r¢
2
 ö
ø 		  ê
ê 		=   æ
Ö
02 + æ
è 		 r¢
2
 ö
ø 		2

 
 
 =  r¢
2
 £  r
2
Toisaalta [`(b)] Î C, koska [`(b)] = (2, 2 + [(r¢)/2]).

2° Joukko B( (2, 2), r) sisältää joukon R2 \C pisteitä, esimerkiksi
c
 
 = æ
è 		2, 2 -  r
2
 ö
ø 		Î (R2 \C)ÇB æ
è 		(2, 2), r ö
ø 		.
Todistus harjoitustehtävä.     [¯]

Joukon A reuna on se joukko
A : = {
x
 
 Î R2   ê
ê 		 
x
 
 on A:n reunapiste }.
Jos [`(x)] Ï A, niin [`(x)] on joukon A reunapiste jos ja vain jos [`(x)] on joukon A kasaantumispiste.

Seuraus 22 [`(A)] = A ÈA.

Joukko A on suljettu jos ja vain jos se sisältää kaikki reunapisteensä.

2  Useamman muuttujan funktiot

Olkoon m, n Î N, A Ì Rm. Funktiota f : A ® R sanotaan m:n muuttujan reaalifunktioksi.

Funktio f : A ® Rn on m:n muuttujan vektoriarvoinen tai Rn-arvoinen funktio. (Jos m = n ³ 2, niin f on vektorikenttä.)

Esimerkki 23 Kahden muuttujan reaaliarvoisia funktioita:
f(x, y)
=
sin(x, y)
f(x, y)
=
x2 + 3x2y - y3
g(x, y)
=
 1
x2 + y2
 -  1
y
h(x, y)
=
tanx1 ·sinx2
h(
x
 
 )
=
ê
ê 		 
x
 
   ê
ê 		+ 3 ê
ê 		 
x
 
   ê
ê 		2
 
g(x1, x2)
=
ì
í
î
1,
x1 ³ x2
sinx1,
x1 < x2
missä x, y Î R ja x1, x2 Î R.

Esimerkki 24 Kahden muuttujan R2-arvoisia funktioita:
f : A ® R2,    f(
x
 
 ) = æ
è 		f1(
x
 
 ), f2(
x
 
 ) ö
ø 		= f1(
x
 
 )
i
 
 + f2(
x
 
 )
j
 
 ,
missä f1 : A ® R, f2 : A ® R ja [`(x)] Î R2. Esimerkiksi
f(x, y)
=
( x2 + y2,  1
x
 +  1
y
 ); x, y Î R    x,y ¹ 0
g(x1, x2)
=
( sinx1 + cosx2, sinx2 - cosx1 ).

Esimerkki 25 Kahden muuttujan R3-arvoisia funktioita:
f(
x
 
 ) = æ
è 		f1(
x
 
 ), f2(
x
 
 ), f3(
x
 
 ) ö
ø 		,
x
 
 Î A Ì R2, fj : A ® R, j = 1, 2, 3,¼
Esimerkiksi
g(x, y)
=
( 2x + y, 3y2, 2x2 )
f(
x
 
 )
=
( sinx1, cos(x1 + x2), tanx2 ).

Yleisesti: Funktio f : A ® Rn, A Ì Rm on muotoa
f(
x
 
 ) = æ
è 		f1(
x
 
 ), f2(
x
 
 ), ¼, fn(
x
 
 ) ö
ø 		,
missä [`(x)] Î A Ì Rm, ja fj : A ® R on funktion f j:s komponenttifunktio.

Esimerkki 26 Ratkaise yhtälö
f(
x
 
 ) = 0, kun f : R3 ® R,    f(x1, x2, x3) = x3 + x12 - 3x23
siis yhtälö
x3 + x12 - 3x23 = 0 Û x3 = 3x23 - x12 (pinta R3:ssa)
Ratkaisu on pinta!

Esimerkki 27 Ratkaise yhtälö
g(
x
 
 ) = (1, 2, 0),    g : R2 ® R3,    g(
x
 
 ) = (x1 + x22, x22, x1)

Ratkaisu. Yhtälöt:
ì
ï
í
ï
î
x1
+
x22
=
1
x23
=
2
x1
=
0
 Û ì
ï
í
ï
î
x23
=
2
x2
=
2
x1
=
0
 Û ì
ï
ï
í
ï
ï
î
x1
=
0
x2
=
3
Ö
 
2
 
x2
=
±1
Yhtälöllä ei siis ole ratkaisua.

Määritelmä 28 Olkoon A Ì R2, [`(a)] Î R2 siten, että B¢([`(a)], r) Ì A. Luku b Î R on funktion f : A ® R raja-arvo pisteessä [`(a)], jos jokaista r > 0 kohti voidaan löytää s > 0 siten, että
ê
ê 		 f(
x
 
 ) - b  ê
ê 		< r,
jos | [`(x)] -[`(a)] | < s, [`(x)] ¹ [`(a)]. Merkitään
b =
lim
[`(x)] ®[`(a)] 
 f(
x
 
 ).

Määritelmä 29 Olkoon joukko B Ì R2 ja piste [`(a)] joukon B kasaantumispiste. Luku b Î R on funktion g : B ® R raja-arvo pisteessä [`(a)] joukossa B, jos jokaista r > 0 vastaa s > 0 siten, että
ê
ê 		 g(
x
 
 ) - b  ê
ê 		< r,
kun [`(x)] Î B ja | [`(x)] -[`(a)] | < s, [`(x)] ¹ [`(a)]. Merkitään
b =
lim
[( [`(x)] ®[`(a)]) || ([`(x)] Î B)]  
 f(
x
 
 ).

Esimerkki 30 Olkoon funktio
f(x, y) : =  x2y2
x2 + y2
määritelty joukossa R2 \{ (0, 0) }. Mikä on funktion f raja-arvo pisteessä 0? Vastaus: 0.

Todistus.  Olkoon r > 0. Arvioidaan lauseketta
ê
ê 		 f(
x
 
 ) - b  ê
ê 		= ê
ê 		 f(
x
 
 )  ê
ê 		.
On näytettävä, että tämä on pienempi kuin r, kunhan [`(x)] on riittävän lähellä origoa. Arvioidaan
ê
ê 		 f(
x
 
 )  ê
ê 		= ê
ê 		   x2y2
x2 + y2
   ê
ê 		£  (x2 + y2)2
x2 + y2
 = (x2 + y2) = ê
ê 		 
x
 
   ê
ê 		2
 
(2)
Valitaan s = min([(r)/2], 1). Olkoon | [`(x)] -[`(a)] | < s eli | [`(x)] | < s. Silloin
ê
ê 		 
x
 
 2
 
   ê
ê 		= ê
ê 		 
x
 
   ê
ê 		· ê
ê 		 
x
 
   ê
ê 		£ ê
ê 		 
x
 
   ê
ê 		< s £  r
2
    [¯]

Esimerkki 31 Määritellään funktio
f(x, y) =  (y2 - x)2
y4 + x2
 ,     (x, y) ¹ (0, 0)
Jos x = y2, niin
f(x, y) =  (y2 - y2)2
y4 + y4
 = 0.
Jos y = kx, k Î R, niin
f(x, y) =  k4 x4 - 2k2 x3 + x2
k4 x4 + x2
 =  1 + k4 x2 - 2k2 x
1 + k2 x2
 ® 1,
kun x ® 0.

Lause 32 Olkoon [`(a)] joukon A kasaantumispiste, sekä joukko B Ì A ja oletetaan, että [`(a)] on myös joukon B kasaantumispiste. Olkoon f : A ® R. Jos on olemassa luku b Î R siten, että

lim
[( [`(x)] ®[`(a)]) || ([`(x)] Î A)]  
 f(
x
 
 ) = b,
niin pätee myös

lim
[( [`(x)] ®[`(a)]) || ([`(x)] Î B)]  
 f(
x
 
 ) = b.

Esimerkki 33 Raja-arvon laskeminen käyriä pitkin. Olkoon g : R2 \{ (0, 0) } ® R ja tarkastellaan raja-arvoa joukossa A Ì R2 \{ (0, 0) }, eli lauseketta

lim
[`(x)] ®[`0],[`(x)] Î A 
 g(
x
 
 )
(3)
a) A : = { (t, kt)  | t Î R, t > 0 } (k kiinteä). Silloin
(3) =
lim
t ® 0+ 
 g(t, kt)
(katso esimerkki 2.0.31).

b) A : = { (t2, t)  | t Î R} Silloin
(3) =
lim
t ® 0 
 g(t2, t).

Esimerkki 34 Olkoon funktio
g(x, y) =  (y2 - x)2
y4 + x2
 .
Nyt

lim
[( [`(x)] ®[`0]) || ([`(x)] ® A)]  
 g(
x
 
 ) =
lim
t ® 0 
 g(t2, t) =
lim
t ® 0 
  (t2 - t2)2
t4 + t4
 = 0.

Huomautus 35 Lauseen 2.0.32 seurauksena funktiolla
f(x, y) =  (y2 - x)2
y4 + x2
ei ole raja-arvoa pisteessä [`0].

Määritelmä 36 Olkoon A Ì Rn ja [`(a)] Î Rn siten, että B¢([`(a)], r) Ì A jollakin r > 0. Funktiolla f : A ® Rm on raja-arvo [`(b)] = (b1, ¼, bn) pisteessä [`(a)] jos jokaista r > 0 vastaa s > 0 siten, että
ê
ê 		 f(
x
 
 ) -
b
 
   ê
ê 		< r, kun ê
ê 		 
x
 
 -
a
 
   ê
ê 		< s,   
x
 
 Î A,
x
 
 ¹
a
 
 .
Vastaavasti määritellään raja-arvo joukossa A, jos piste [`(a)] on joukon A kasaantumispiste.

Lause 37 Olkoon A,[`(a)],[`(b)], f : = { f1, ¼, fm }, kuten Määritelmässä 2.0.36. Piste [`(b)] on funktion f raja-arvo pisteessä [`(a)], jos ja vain jos

lim
[`(x)] ®[`(a)] 
 fk(
x
 
 ) = bk,     1 £ k £ m.

Todistus.  Oletetaan

lim
[`(x)] ®[`(a)] 
 f(
x
 
 ) =
b
 
 .
(4)
Olkoon k Î { 1, ¼, m }. On osoitettava että

lim
[`(x)] ®[`(a)] 
 fk(
x
 
 ) =
b
 
k 
 .
Olkoon r > 0. On löydettävä s > 0 siten, että | fk([`(x)]) - bk | < r, kun | [`(x)] -[`(a)] | < s. Koska (4) pätee, niin on olemassa s > 0 siten, että | f([`(x)]) -[`(b)] | < r, kun | [`(x)] -[`(a)] | < s. Tällöin
ê
ê 		 fk(
x
 
 ) - bk  ê
ê 		=   æ
Ö
ê
ê 		 fk(
x
 
 ) - bk  ê
ê 		2
 
 
 £   æ
Ö
m
å
j = 1 
 ê
ê 		 fj(
x
 
 ) - bj  ê
ê 		2
 
 
 = ê
ê 		 f(
x
 
 ) -
b
 
   ê
ê 		< r.

Oletetaan toisaalta, että

lim
[`(x)] ®[`(a)] 
 fk(
x
 
 ) = bk
(5)
pätee kaikille k. Olkoon r > 0. Valitaan sk > 0 siten, että | fk([`(x)]) - bk | < [(r)/(m)], kun | [`(x)] -[`(a)] | < sk. Valitaan s = min1 £ k £ m sk. Jos | [`(x)] -[`(a)] | < s, niin
ê
ê 		 f(
x
 
 ) -
b
 
   ê
ê 		=   æ
Ö
m
å
k = 1 
 ê
ê 		 fk(
x
 
 ) - bk  ê
ê 		2
 
 
 £ m
å
k = 1 
 ê
ê 		 fk(
x
 
 ) - bk  ê
ê 		< m
å
k = 1 
  r
m
 = m  r
m
 = r.
    [¯]

Esimerkki 38 Olkoon joukko A = R\{ (0, 1, 0) }, m = 2, ja
f(x1, x2, x3)
=
æ
è 		x1 + sin(x2 x3),  x14(x2 - 1)4 x34
x12 + (x2 - 1)2 + x32
 ö
ø
f1(x1, x2, x3)
=
x1 + sin(x2 x3)     (A ® R)
f2(x1, x2, x3)
=
 x14(x2 - 1)4 x34
x12 + (x2 - 1)2 + x32
     (A ® R).
Tässä f1 ja f2 ovat kuvauksia A ® R. Laske lim[`(x)] ® (0, 1, 0) f([`(x)]).

Lauseen 2.0.37 mukaan on syytä tarkastella komponenttifunktioita erikseen:

lim
[`(x)] ® (0, 1, 0) 
 f1(x1, x2, x3) =
lim
[`(x)] ® (0, 1, 0) 
 x1 + sin(x2 x3) = 0 + sin0 = 0.
Voidaan olettaa, että | x1 | £ 1, | x2 - 1 | £ 1 ja | x3 | £ 1. Tästä seuraa
| x14(x2 - 1)4 x34 | = | x1 |4 | x2 - 1 |4 | x3 |4 £ | x1 |2 | x2 - 1 |2 | x3 |2 £ (x12 + (x2 - 1)2 + x32))3.
Siis,
ê
ê 		   x14(x2 - 1)4 x34
x12 + (x2 - 1)2 + x32
   ê
ê
£
ê
ê 		   (x12 + (x2 - 1)2 + x32))3
x12 + (x2 - 1)2 + x32
   ê
ê 		= (x12 + (x2 - 1)2 + x32))2
=
ê
ê 		 
x
 
 - (0, 1, 0)  ê
ê 		4
 
 ® 0,
kun [`(x)] ® (0, 1, 0), eli | [`(x)] - (0, 1, 0) | ® 0. Näin ollen

lim
[`(x)]® (0, 1, 0) 
 f(
x
 
 ) = 0

Lause 39 Oletetaan, että kuvauksille f, g : A ® Rn pätee

lim
[`(x)] ®[`(a)] 
 f(
x
 
 ) =
b
 
 ,   
lim
[`(x)] ®[`(a)] 
 g(
x
 
 ) =
c
 
 .
Tällöin

Määritelmä 40 Olkoon A Ì Rm ja f : A ® Rn. Sanotaan, että funktio f on jatkuva pisteessä [`(a)] Î A, jos annetulle mielivaltaiselle r > 0 voidaan löytää s > 0 seuraavasti:
ê
ê 		 f(
x
 
 ) - f(
a
 
 )  ê
ê 		< r, kun ê
ê 		 
x
 
 -
a
 
   ê
ê 		< s,
x
 
 Î A.
Funktio f on jatkuva joukossa A jos se on jatkuva jokaisessa joukon A pisteessä.

Esimerkki 41 Funktio f(x, y) = x2 + 3yx + y10, f : R2 ® R on jatkuva. Yleisesti n:n muuttujan reaaliarvoinen polynomi on jatkuva.

Esimerkki 42 Funktio
g : =  3xy + y + px2
x2 - y2
 ,     g : A ® R,    A = { (x, y)   ê
ê 		 x2 ¹ y2 }
on jatkuva joukossa A.

Lause 43 Kuvaus f = (f1, ¼, fn) : A ® Rn on jatkuva pisteessä [`(a)] jos ja vain jos fk : A ® R on jatkuva pisteessä [`(a)] kaikilla k = 1, ¼, n.

Esimerkki 44 Olkoon funktio f(x, y, z) = (x2 z2, y + 3z). Tässä f1(x, y, z) = x2 z2 on jatkuva ja f2(x, y, z) = y + 3z on jatkuva, joten funktio f on jatkuva R:ssä.

Analogisesti Lauseen 2.0.39 kanssa, kahden jatkuvan funktion summa, skalaaritulo, jne... ovat jatkuvia.

Huomautus 45 Olkoot f : A ® B, g : B ® C, missä A, B, C ovat joukkoja:
g °f(x) : = g ( f(x) ),
kun x Î A. Siis g °f : A ® C.

Lause 46 Olkoon A Ì Rn, B Ì Rn, f : A ® Rn siten, että f(A) Ì B ja g : B ® Rk. Oletetaan edelleen että joukko B on avoin, piste [`(a)] Î A, funktio f on jatkuva pisteessä [`(a)] ja funktio g on jatkuva pisteessä f([`(a)]). Silloin funktio g °f on jatkuva pisteessä [`(a)].

Esimerkki 47 Määritellään funktio f(x, y) = (x2, y), R2 ® R2. Se on jatkuva ja sen iteraateille pätee

Kaikki nämä ovat jatkuvia.

Esimerkki 48 Määritellään funktio f(x, y) = (y, x2), R2 ® R2 joka on jatkuva.

3  Differentiaalilaskenta

3.1  Osittaisderivaatta

Määritelmä 1 Olkoon [`(a)] = (a1, a2) Î R2 ja f reaaliarvoinen funktio, joka on määritelty ainakin [`(a)]:n jossakin ympäristössä. Jos on olemassa raja-arvo

lim
h ® 0 
  f(a1 + h, a2) - f(a1, a2)
h
 ,
niin tätä sanotaan funktion f osittaisderivaataksi 1. muuttujan suhteen (tai x:n suhteen) pisteessä [`(a)]. Merkitään
D1f(
a
 
 ),      f
x1
 (
a
 
 ),     f
x
 (
a
 
 ),     fx1(
a
 
 ),    f¢x1(
a
 
 ).
Vastaavasti määritellään f:n osittaisderivaatta toisen muuttujan suhteen raja-arvona

lim
h ® 0 
  f(a1, a2 + h) - f(a1, a2)
h
Tätä merkitään
D2 f(
a
 
 ),      f
x2
 (
a
 
 ),     f
y
 (
a
 
 ) jne.
Sanotaan, että funktio f on derivoituva pisteessä [`(a)], jos derivaatat D1 f ([`(a)]) ja D2 f ([`(a)]) ovat olemassa. Jos funktio f on derivoituva joukon A jokaisessa pisteessä, niin f on derivoituva joukossa A.

Esimerkki 2 Olkoon
f(x, y) = ì
ï
í
ï
î
0
kun (x, y) = (1, 0)
 xy3
(x - 1)2 + y2
 ,
kun (x, y) ¹ (1, 0)
Tällöin
D1 f (1, 0) =
lim
h ® 0 
  f(1 + h, 0) - f(1, 0)
h
 =
lim
h ® 0 
  0 - 0
h
 = 0
ja
D2 f (1, 0) =
lim
h ® 0 
  f(1, h) - f(1, 0)
h
 =
lim
h ® 0 
  h3
h2h
 =
lim
h ® 0 
 1 = 1.
Olkoon f kuten yllä. Pitäen muuttujaa y kiinteänä määritellään x:n funktio g(x) : = f(x, y). Silloin
g¢(x) =
lim
h ® 0 
  g(x + h), y) - g(x)
h
 =
lim
h ® 0 
  f(x + h, y) - f(x, y)
h
 =  f
x
 (x, y).

Näemme siis, että osittaisderivaatta x:n suhteen voidaan muodostaa tuttuja derivoimissääntöjä käyttäen (pitämällä y vakiona).

Esimerkki 3 Jos
f(x, y) = x3y2 + x4 siny,
on osittaisderivaatta
D1 f(x, y) = 3y2 x2 + 4 x3 siny.
Jos
g(x, y) = y2 + exy,
on osittaisderivaatta
D1 g(x, y) = 0 + exy ·  (xy)
x
 = exyy.
Vastaavasti [()/(y)] muodostetaan pitämällä x:ää vakiona (f ja g kuten yllä):
D2 f(x, y)
=
2x3y + x4 cosy,
D2 g(x, y)
=
2y + xexy.

Useamman muuttujan funktion osittaisderivaatat

Olkoon funktio g määritelty pisteen [`(a)] =(a1, ¼, an) Î Rn ympäristössä, ja j Î { 1, ¼, n }. Raja-arvot
 g
xj
 =
lim
h ® 0 
  g(a1, ¼, aj + h, ¼, an) - g(a1, ¼, aj, ¼, an)
h
on osittaisderivaatta j:nen muuttujan suhteen, ja sitä merkitään Dj g([`(a)]).

Esimerkki 4 Määritellään funktio
f(x1, x2, x3, x4) = x12 x3 + sin(x2 + x4) + ex1 + x4.
Sen osittaisderivaatat ovat
D1 f
=
2x1 x3 + 0 + ex1 + x4 ·

D1(x1 + x4)
= 1 
 = 2x1 x3 + ex1 + x4
D2 f
=
0 + cos(x2 + x4) + 0 = cos(x2 + x4)
D3 f
=
x12
D4 f
=
cos(x2 + x4) + ex1 + x4.

Huomautamme, että derivoituvan funktion ei tarvitse olla jatkuva.

Esimerkki 5 Funktio
f(x, y) = ì
ï
í
ï
î
1,
kun x = 0 Ú
y = 0
0,
muulloin
ei ole jatkuva pisteessä [`0] = (0, 0), mutta
D1 f(0, 0) =
lim
h ® 0 
  f(h, 0) - f(0, 0)
h
 =
lim
h ® 0 
  1 - 1
h
 = 0,    D2 f(0, 0) = 0.

3.2  Korkeamman kertaluvun derivaatat

Jos derivaatta Dj f on olemassa pisteen [`(a)] ympäristössä ja Dj f on derivoituva k:nen muuttujan suhteen, saadaan 2. kertaluvun osittaisderivaatta
Djk f(
a
 
 ) = æ
è 		Dk (Dj f) ö
ø 		(
a
 
 )
(j, k Î { 1, ¼, n }, kun f on n:n muuttujan funktio). Merkitään myös
 2 f
xj xk
 (
a
 
 ).
Vastaavasti määritellään funktion f korkeamman kertaluvun osittaisderivaatat
Djki f : = Di (Djk f)
ja niin edelleen. Sanotaan, että f on m kertaa jatkuvasti derivoituva, jos kaikki enintään kertalukua m olevat osittaisderivaatat ovat olemassa ja jatkuvia.

Esimerkki 1 Funktion
f(x, y, z) : = x3y2 + x4siny + cos(xz)
osittaisderivaatat ovat
D1 f
=
3y2x2 + 4x3siny - zsin(xz)
D2 f
=
2x3y + x4cosy
D3 f
=
-xsin(xz).
Päteekö D12 = D21?
D11 f
=
6xy2 + 12x2siny - z2cos(xz)
D22 f
=
2x3 - x4siny
D33 f
=
-x2cos(xz)
D12 f
=
D2(D1 f) = 6x2y + 4x3cosy
D21 f
=
D1(D2 f) = 6x2y + 4x3cosy
D13 f
=
D3(D1 f) = -sin(xz) - xz cos(xz)
D31 f
=
D1(D3 f) = -sin(xz) - xz cos(xz)
D23 f
=
0
D32 f
=
0.

Esimerkki 2 Määritellään funktio
f(x, y) : = ì
ï
ï
í
ï
ï
î
 xy(x2 - y2)
x2 + y2
 ,
kun (x, y) ¹
0
 
0
kun (x, y) =
0
 
 .
Kun (x, y) ¹ (0, 0):
D1 f = D1 æ
è 		 xy(x2 - y2)
x2 + y2
 ö
ø
=
 (3x2y - y3)(x2 + y2) - 2x(x3y - xy3)
(x2 + y2)2
=
 4x2y3 + x4y - y5
(x2 + y2)2
(6)
ja
D2 f = ¼ =  x5 - 4x3y2 - xy4
(x2 + y2)2
 .
(7)
Tuloksesta (6) seuraa
D1 f(0, y) =  0 ·y3 + 0 ·y - y5
(02 + y2)2
 =  -y5
y4
 = -y,     kun y ¹ 0,
(8)
ja tuloksesta (7)
D2 f(x, 0) = ¼ = x,     x ¹ 0.
(9)
Osittaisderivaatat origossa ovat
D1f(0, 0) =
lim
h ® 0 
  f(h, 0) - f(0, 0)
h
 =
lim
h ® 0 
 h ·0 ·(h2 - 02)
h2 + 0
 - 0
h
 =
lim
h ® 0 
  0
h
 = 0
(10)
ja
D2 f(0, 0) =
lim
h ® 0 
  f(0, h) - f(0, 0)
h
 = ¼ = 0.
(11)
Nyt tuloksien (8) ja (10) avulla saadaan
D12 f(0, 0) = D2(D1 f)(0, 0) =
lim
h ® 0 
  D1 f(0, h) - D1 f(0, 0)
h
 =
lim
h ® 0 
  -h - 0
h
 = -1
ja tuloksista (9) ja (11)
D21 f(0, 0) = D1(D2 f)(0, 0) =
lim
h ® 0 
  D2 f(h, 0) - D2 f(0, 0)
h
 =
lim
h ® 0 
  h - 0
h
 = 1.
On kuitenkin vain erikoistapaus, että osittaisderivaatat saavat eri arvot.

Lause 3 Olkoon funktio f reaaliarvoinen kuvaus, joka on määritelty pisteen (a, b) Î R2 ympäristössä. Oletetaan, että D12 f ja D21 f ovat olemassa pisteen (a, b) ympäristössä ja jatkuvia ainakin pisteessä (a, b). Silloin
D12 f(a, b) = D12 f(a, b).

Todistus sivuutetaan.

Esimerkki 4 Olkoon
f(x, y) = x2y + exy.
Osittaisderivaatat
D1
=
2xy + yexy
D2
=
x2 + xexy
D21
=
2x + exy(1 + xy)
D12
=
2x + exy(1 + xy)

Olkoon f = (f1, ¼, fn) pisteen [`(a)] Î Rm ympäristössä määritelty vektoriarvoinen kuvaus. Määritellään funktion f osittaisderivaatta xj:n suhteen pisteessä [`(a)] raja-arvona
Dj f(
a
 
 ) =
lim
h ® 0 
  f(a1, ¼, aj + h, ¼, am) - f(a1, ¼, am)
h
mikäli raja-arvo on olemassa. Ei ole vaikea osoittaa, että osittaisderivaatta saadaan derivoimalla komponenttifunktiot:
Dj f(
a
 
 ) = æ
è 		Dj f1(
a
 
 ), ¼, Dj fn(
a
 
 ) ö
ø 		.

Esimerkki 5 Olkoon m = 2, n = 3 ja
f(x, y) = æ
è 		sin(x + y), x2, exy ö
ø 		.
Osittaisderivaatat ovat
D1 f(x, y)
=
æ
è 		cos(x + y), 2x, yexy ö
ø
D2 f(x, y)
=
æ
è 		cos(x + y), 0, xexy ö
ø 		.

Lause 6 Olkoon funktio f määritelty pisteessä [`(a)] Î Rm, reaaliarvoinen. Jos osittaisderivaatat Dij f ja Dji f, i < j, ovat olemassa pisteen [`(a)] ympäristössä ja jatkuvia pisteessä [`(a)], niin
Dij f(
a
 
 ) = Dji f(
a
 
 ),     i, j Î {1, ¼, m}.

Todistus.  Olkoon [`(a)] = (a1, ¼, am). Määritellään
g(x, y) : = f(a1, ¼, ai - 1, x, ai + 1, ¼, aj - 1, y, aj + 1, ¼, am)
joka on kahden muuttujan funktio. Funktiolle g pätee: x on määritelty pisteen [`(a)]¢ = (ai, aj) Î R2 ympäristössä, D1 g, D2 g määritelty [`(a)]¢:n ympäristössä jne... Sovelletaan lausetta 3.2.3.
Dij f(
a
 
 ) = D12 g(ai, aj) = D21 g(aj, ai) = Dji f(
a
 
 ).
    [¯]

Esimerkki 7 Jos h : R4 ® R ja kaikki osittaisderivaatat kertalukuun 5 asti ovat jatkuvia, niin
D1234 h = D4321 h = D1432 h = ¼
Mutta tietenkään ei päde esimerkiksi D213 h = D223 h.

3.3  Differentioituvuus

Yhden muuttujan funktio f on derivoituva pisteessä x0 Î R jos ja vain jos on olemassa a Î R siten, että
f(x0 + h) - f(x0) = ah + he(h),
missä e on reaalimuuttujan funktio, määritelty 0:n ympäristössä ja e(h) ® 0, kun h ® 0. Silloin a = Df(x0).

Tutkitaan samaa asiaa kahden muuttujan funktioille. Olkoon [`(a)] = (a1, a2) tarkastelupiste ja oletetaan, että funktio f on määrätty pisteen [`(a)] jossakin ympäristössä U. Oletetaan, että [`(h)] Î R siten, että [`(a)]+ [`(h)] Î U.

Määritelmä 1 Funktio f on differentioituva pisteessä [`(a)], jos on olemassa luvut a1 ja a2 siten, että
f(
a
 
 +
h
 
 ) - f(
a
 
 ) = a1 h1 + a2 h2 + ê
ê 		 
h
 
   ê
ê 		e(
h
 
 ),
(12)
missä e on jossain origon ympäristössä V määritelty funktio V ® R ja e([`(h)]) ® 0 kun [`(h)]®[`0]. Jos merkitään [`(a)] = (a1, a2), niin (12) voidaan kirjoittaa muodossa
f(
a
 
 +
h
 
 ) - f(
a
 
 ) =
a
 
 ·
h
 
 + ê
ê 		 
h
 
   ê
ê 		e(
h
 
 ).

Määritelmä 2 Olkoon A Î R2. Funktio f: A ® R on differentioituva joukossa A, jos se on differentioituva jokaisessa pisteessä [`(a)] Î A.

Lause 3 Jos funktio f on differentioituva pisteessä [`(a)], niin se on jatkuva pisteessä [`(a)].

Todistus.  Olkoon s > 0. On löydettävä r > 0 siten, että
ê
ê 		 f(
x
 
 ) - f(
a
 
 )  ê
ê 		< s, kun ê
ê 		 
x
 
 -
a
 
   ê
ê 		< r.
Olkoon e kuten kaavassa (12), samoin [`(a)] = (a1, a2). Voidaan löytää s¢ siten, että | e(h) | < 1, kun | [`(h)] | < s¢. Valitaan r = min( s¢, [(s)/(| [`(a)] | + 1)] ). Olkoon nyt [`(x)] sellainen, että | [`(x)]- [`(a)] | < r. Tällöin (merkitään [`(h)] = [`(x)]- [`(a)])
ê
ê 		 f(
x
 
 ) - f(
a
 
 )  ê
ê
=
ê
ê 		 f(
a
 
 +
h
 
 ) - f(
a
 
 )  ê
ê 		= ê
ê 		 
a
 
 ·
h
 
 + ê
ê 		 
h
 
   ê
ê 		e(
h
 
 )  ê
ê
£
ê
ê 		 
a
 
 ·
h
 
   ê
ê 		+ ê
ê 		 
h
 
   ê
ê 		ê
ê 		 e(
h
 
 )  ê
ê 		£ ê
ê 		 
h
 
   ê
ê 		æ
è 		ê
ê 		 
a
 
   ê
ê 		+ ê
ê 		 e(
h
 
 )  ê
ê 		ö
ø
£
ê
ê 		 
x
 
 -
a
 
   ê
ê 		æ
è 		ê
ê 		 
a
 
   ê
ê 		+ 1 ö
ø 		< r æ
è 		ê
ê 		 
a
 
   ê
ê 		+ 1 ö
ø 		£  s
ê
ê 		 
a
 
   ê
ê 		+ 1
 æ
è 		ê
ê 		 
a
 
   ê
ê 		+ 1 ö
ø 		= s.
    [¯]

Lause 4 Jos funktio f on differentioituva pisteessä [`(a)], niin f on derivoituva ja
Dj f(
a
 
 ) = aj,     j = 1, 2

Todistus.  Tapaus j = 1.
f(
a
 
 +
h
 
 ) - f(
a
 
 ) = a1 h1 + a2 h2 + ê
ê 		 
h
 
   ê
ê 		e(
h
 
 ),
missä e([`(h)]) ® 0 kun [`(h)]® 0. Tämä pätee, kun [`(h)] on jossakin [`0]:n ympäristössä. Erityisesti voidaan tarkastella tapausta [`(h)] = (h1, 0), missä h1 > 0. Muodostetaan
f(
a
 
 +
h
 
 ) - f(
a
 
 )
h1
=
 f(a1 + h1, a2) - f(a1, a2)
h1
 =  a1 h1
h1
 +
ê
ê 		 
h
 
   ê
ê
h1
 e(
h
 
 )
=
a1 +
ê
ê 		 
h
 
   ê
ê
h1
 e(
h
 
 ) ® a1,
kun [`(h)]®[`0]. Tämä todistaa, että D1 f([`(a)]) = a1, koska osittaisderivaatan määritelmän mukaan on toisaalta

lim
h1 ® 0 
  f(a1 + h1, a2) - f(a1, a2)
h1
 = D1 f(
a
 
 ).
Toinen muuttuja käsitellään vastaavasti.     [¯]

Differentioituvuus ja muut edellä mainitut tulokset määritellään ja todistetaan samalla tavalla n:n muuttujan funktioille.

Esimerkki 5 Funktion
f(x, y) = ì
ï
ï
í
ï
ï
î
 xy

Ö
x2 + y2
 ,
kun (x, y) ¹ (0, 0)
0,
kun (x, y) = (0, 0).
molemmat osittaisderivaatat D1 f(x, y), D2 f(x, y) saavat origossa arvon 0. Voidaan kuitenkin osoittaa, ettei f ole differentioituva origossa.

Lause 6 Jos funktio f on derivoituva jossakin pisteen [`(a)] ympäristössä ja osittaisderivaatat ovat jatkuvia pisteessä [`(a)], niin f on differentioituva pisteessä [`(a)].

Esimerkki 7 Onko funktio f(x, y, z) : = x2y| z | + xy differentioituva pisteessä (2, 0, 0)?

Ratkaisu.
D1 f(x, y, z)
=
2xy| z | + y
D2 f(x, y, z)
=
x2| z | + x
D3 f(x, y, z)
=

lim
h ® 0 
  f(2, 0, n) - f(2, 0, 0)
h
 =
lim
h ® 0 
  0 - 0
h
 = 0
D1 f(2, 0, 0)
=
0
D2 f(2, 0, 0)
=
2
Funktio f on siis derivoituva pisteessä (2, 0, 0). Funktio f on differentioituva pisteessä (2, 0, 0), jos
f(2 + h1, h2, h3) - f(2, 0, 0) = D1 f(2, 0, 0)h1 +D2 f(2, 0, 0)h2 + D3 f(2, 0, 0)h3 + ê
ê 		 
h
 
   ê
ê 		e(
h
 
 ),
missä e® 0 kun | [`(h)] | ® 0. Ratkaistaan tästä e ja tutkitaan sen käyttäytymistä, kun | [`(h)] | ® 0.
e(
h
 
 )
=
 f(2 + h1, h2, h3) - f(2, 0, 0) - 2h2
ê
ê 		 
h
 
   ê
ê
=
 (2 + h1)2h2| h3 | + (2 + h1)h2 - 2h2

Ö
h12 + h22 + h32
=
(2 + h1)2| h3 |  h2

Ö
h12 + h22 + h32
 + h1  h2

Ö
h12 + h22 + h32
£
(2 + h1)2 | h3 | + | h1 | ® 0
kun [`(h)]® 0. Tässä
 | h2 |

Ö
h12 + h22 + h32
 £ 1,
joten funktio f on differentioituva.

Lauseke
D1 f(
a
 
 )h1 + D2 f(
a
 
 )h2 + ¼+ Dn f(
a
 
 )hn
on nimeltään funktion f differentiaali pisteessä [`(a)], merkitään d f([`(a)])([`(h)]). Pätee siis
\triangle f = f(
a
 
 +
h
 
 ) - f(
a
 
 ) » d f(
a
 
 )(
h
 
 ),
kun [`(h)] on "pieni".

Esimerkki 8 Funktion f(x, y) = x3y2 osittaisderivaatat ovat
D1 f = 3x2y2     ja     D2 f = 2x3y.
Kun [`(a)] = (a1, a2) = (1, 2) ja [`(h)] = (h1, h2) = (-0.04, 0.05) on funktion f differentiaali
d f(
a
 
 )(
h
 
 ) = D1 f(1, 2) ·(-0.04) + D2 f(1, 2) ·0.05 = ¼ = -0.28
ja
\triangle f = f(0.96, 2.05) - f(1, 2) = 0.963 ·2.05 - 4 » -0.2819¼

Esimerkki 9 (Virhearviointi) Pyritään määräämään maan vetovoiman kiihtyvyys (g) kokeellisesti, mittaamalla putoamisaikaa t ja putoamismatkaa s.
s =  1
2
 gt2 Þ g =  2s
t2
 .
Mittaustulokset s ja t eroavat jonkin verran todellisista arvoista s + h1, s + h2. Tällöin g:n virhe
\triangle g = g(s + h1, t + h2) - g(s, t) » d g(s, t)(
h
 
 ) =  g
s
 h1 +  g
t
 h2 =  2
t2
 h1 -  4s
t3
 h2.
Jos tiedetään mittaustarkkuudet eli | h1 | £ d (jokin vakio) ja | h2 | £ t (myös jokin vakio), niin
ê
ê 		 dg(s, t)(
h
 
 )  ê
ê 		£  2
t2
 d+  4| s |
t3
 t.

(Huomatus! Osittaisderivaatan jatkuvuudesta seuraa siis differentioituvuus, josta taas seuraa osittaisderiviutuvuuden olemassaolo.)

3.4  Gradientti ja suunnatut derivaatat

Määritelmä 1 Olkoon A Ì °  R2 ja f: A ® R, differentioituva. Tällöin funktion f gradientti on vektoriarvoinen funktio A ® R2, Merkitään
gradf = Ñf : = (D1 f, D2 f) = D1 f
^
i
 
 + D2 f
^
j
 
 .
Yleensä, jos A Ì °  Rn, f : A ® R niin määritellään
Ñf : = (D1 f, D2 f, ¼, Dn f).
Pätee
df(
a
 
 )(
h
 
 ) = D1 f (ya)h1 + D2 f(
a
 
 )h2 = æ
è 		D1 f(
a
 
 ), D2 f(
a
 
 ) ö
ø 		·(h1, h2) = Ñf (
a
 
 ) ·
h
 
 ,
missä [`(h)] = (h1, h2). Myös avaruudessa Rn
df(
a
 
 )(
h
 
 ) = Ñf(
a
 
 ) ·
h
 
 .

Olkoon [`(a)] = (a1, a2) Î R2 siten, että | [`(a)] | = 1 = Ö{a12 + a22}. Olkoon funktio f pisteen [`(a)] = (a1, a2) ympäristössä määritelty reaaliarvoinen funktio. Joukko
ì
í
î
a
 
 + t
a
 
   ê
ê 		 t Î R ü
ý
þ
on pisteen [`(a)] kautta kulkeva [`(a)]:n suuntainen suora.

Määritelmä 2 Jos on olemassa raja-arvo

lim
t ® 0 
f(
a
 
 + t
a
 
 ) - f(
a
 
 )
t
 ,
niin sitä kutsutaan derivaataksi suuntaan [`(a)] (pisteessä [`(a)]), merkitään [`(a)] f([`(a)]).

Huomautus 3 Jos [`(a)] = (0, 1) = [^(j)], niin [`(a)] f([`(a)]) = D2 f.

Huomautus 4 Määritelmä 3.4.2 on sama Rn:ssä.

Lause 5 Jos f on differentioituva pisteessä [`(a)], niin [`(a)] f([`(a)]) on olemassa jokaiseen suuntaan [`(a)] ja
[`(a)] f(
a
 
 ) = D1 f(
a
 
 ) a1+ D2 f(
a
 
 ) a2 + ¼+ Dn f(
a
 
 ) an = Ñf(
a
 
 ) ·
a
 
 .

Lause todistetaan myöhemmin.

Esimerkki 6 Laske funktion
f(x, y, z) : = x4 + x3y + 2x2z
derivaatta pisteessä (1, 2, 5) vektorin (4, -2, 2) suuntaan.

Ratkaisu. Lasketaan vektorin (4, -2, 2) = [`(v)] suuntainen yksikkövektori
a
 
 =
v
ê
ê 		 
v
 
   ê
ê
=  (4, -2, 2)

Ö
42 + 22 + 22
 = æ
è 		 2
Ö6
 ,  -1
Ö6
 ,  1
Ö6
 ö
ø 		.
Osittaisderivaatat ovat
D1 f
=
4x3 + 3x2y + 4xz;
D1 f(1, 2, 5)
=
30
D2 f
=
x3;
D2 f(1, 2, 5)
=
1
D3 f
=
2x2;
D3 f(1, 2, 5)
=
2,
mistä seuraa
Ñf(1, 2, 5)
=
(30, 1, 2)
[`(a)] f(1, 2, 5)
=
(30, 1, 2) · æ
è 		 2
Ö6
 , -  1
Ö6
 ,  1
Ö6
 ö
ø 		=  61
Ö6
 .

Lauseen 3.4.5 todistus:

Olkoon [`(a)] tarkastelupiste, jossa funktio f on differentioituva ja olkoon [`(a)] Î Rn, | [`(a)] | = 1 ja t Î R. Koska funktio f on differentioituva, niin
f(
a
 
 + t
a
 
 ) - f(
a
 
 ) = D1 f(
a
 
 )ta1 + ¼+ Dn f(
a
 
 )tan+ | t | ê
ê 		 
a
 
   ê
ê 		e(t
a
 
 ).
Siis erotusosamäärä
f(
a
 
 + t
a
 
 ) - f(
a
 
 )
t
 = D1 f(
a
 
 )a1 + ¼+ Dn f(
a
 
 )an+  | t |
t
 e(t
a
 
 )

®D1 f(
a
 
 )a1 + ¼+ Dn f(
a
 
 )an
kun t ® 0. Raja-arvo on siis olemassa, joten on olemassa suunnattu derivaatta, joka on
D1 f(
a
 
 )a1 + ¼+ Dn f(
a
 
 )an = Ñf(
a
 
 ) ·
a
 
 .        [¯]

Huomautus 7 Suunnatulle derivaatalle saadaan arvio
ê
ê 		 [`(a)] f(
a
 
 )  ê
ê
=
ê
ê 		 Ñf(
a
 
 ) ·
a
 
   ê
ê
£
ê
ê 		 Ñf(
a
 
 )  ê
ê 		ê
ê 		 
a
 
   ê
ê 		= ê
ê 		 Ñf(
a
 
 )  ê
ê
=
  æ
Ö
(D1 f(
a
 
 )a1)2 + ¼+ (Dn f(
a
 
 )an)2
 
 .
Erityisesti, jos Ñf([`(a)]) = 0, niin [`(a)] f([`(a)]) = 0 kaikkiin suuntiin a. Jos Ñf([`(a)]) ¹ 0, niin voidaan kysyä, mihin suuntaan [`(a)] saadaan suurin derivaatta. Vastaus: Kun [`(a)] ­­ Ñf([`(a)]) eli
a
 
 =
Ñf(
a
 
 )
ê
ê 		 Ñf(
a
 
 )  ê
ê
;
silloin pätee
[`(a)] f(
a
 
 ) = Ñf(
a
 
 ) ·
a
 
 = Ñf(
a
 
 ) ·
Ñf(
a
 
 )
ê
ê 		 Ñf(
a
 
 )  ê
ê
=
ê
ê 		 Ñf(
a
 
 )  ê
ê 		2
 
ê
ê 		 Ñf(
a
 
 )  ê
ê
= ê
ê 		 Ñf(
a
 
 )  ê
ê 		.

3.5  Yhdistettyjen kuvausten derivoiminen

Määritelmä 1 Vektoriarvoista funktiota
g : = (g1, ¼, gn),     g : Rm ® Rn, gj : Rm ® R
sanotaan differentioituvaksi pisteessä [`(a)], jos jokainen komponenttifunktio gj on differentioituva pisteessä [`(a)].

Lause 2 (Ketjusääntö) Olkoon g : Rm ® Rn, g = (g1, ¼, gn) pisteessä [`(a)] differentioituva funktio ja f : U ® R, g([`(a)]) Î U Ì °  Rn pisteessä g([`(a)]) differentioituva funktio. Tällöin f °g on differentioituva pisteessä [`(a)] ja
Di (f °g) = n
å
j = 1 
 æ
è 		Dj f ö
ø 		æ
è 		g(
a
 
 ) ö
ø 		æ
è 		Di gj ö
ø 		(
a
 
 ),
missä i = 1, ¼, m.

Esimerkki 3 Olkoot funktiot f : R® R ja g : R® R. Nyt
D(f °g)(a) = f¢ æ
è 		g(a) ö
ø 		·g(a).

Esimerkki 4 Olkoot m = 1, n = 2, f : R2 ® R, g : R® R2, f(x, y) = x2 + ey + exy ja g(t) = (t, 1 - t) = (g1(t), g2(t)). Nyt
f °g : R® R,     f °g(t) = t2 + e1 - t + et(1 - t)
ja
D(f °g)(t) = 2t - e1 - t + (1 - 2t)et - 2t.
Lauseen 3.5.2 avulla:
ì
í
î
D1 f(x, y)
=
2x + yexy
D2 f(x, y)
=
ey + xexy
 ,     ì
í
î
Dg1(t)
=
1
Dg2(t)
=
-1,
joten
D(f °g)(t)
=
(D1 f) æ
è 		g(t) ö
ø 		·(Dg1)(t) + (D2 f) æ
è 		g(t) ö
ø 		·(Dg2)(t)
=
æ
è 		2t + (1 - t)et(1 - t) ö
ø 		·1 + æ
è 		e1 - t + tet(1 - t) ö
ø 		·(-1)
=
2t - e1 - t + (1 - 2t)et - 2t.
Jos g (sisäfunktio) on yhden muuttujan funktio, niin f °g on myös yhden muuttujan funktio ja
D æ
è 		f °g ö
ø 		= n
å
j = 1 
 (Dj f) æ
è 		g(t) ö
ø 		g¢(t).

Esimerkki 5 Oletetaan että n = 1, n Î N ja funktio f on yhden muuttujan funktio, g skalaariarvoinen funktio. Tällöin f °g on m:n muuttujan funktio,
f °g (x1, ¼, xm) = f æ
è 		g(x1, ¼, xm) ö
ø
ja
Di f °g (
x
 
 ) = f¢ æ
è 		g(
x
 
 ) ö
ø 		·Di g(
x
 
 ),     i = 1, ¼, m,
x
 
 = (x1, ¼, xn) Î Rn.

Esimerkki 6 Määritellään funktiot f ja g siten, että
f : R® R,
f(x)
=
x2 + sinx
g : R3 ® R,
g(
x
 
 )
=
x1 - x2 + x32.
Nyt n = 1, m = 3 ja [`(x)] = (x1, x2, x3) Î R3. Yhdistetty kuvaus f °g : R3 ® R on
f °g(
x
 
 ) = (x1 - x2 + x32)2 + sin(x1 - x2 + x32).
Lasketaan tämän osittaisderivaatat:
f¢(x) = 2x + cosx
ja
D1 g(
x
 
 ) = 1,     D2 g(
x
 
 ) = -1 ja D3 g(
x
 
 ) = 2x3,
joten
D1(f °g)(
x
 
 )
=
æ
è 		2(x1 - x2 + x32) + cos(x1 - x2 + x32) ö
ø 		·1
D2(f °g)(
x
 
 )
=
-2(x1 - x2 + x32) - cos(x1 - x2 + x32)
D3(f °g)(
x
 
 )
=
2x3 ·2(x1 - x2 + x32) + 2x3 cos(x1 - x2 + x32).

Lauseen 3.5.2 todistuksen idea:

Valitaan [`(a)] Î Rm tarkastelupiste, [`(h)] Î Rm "pieni muutos".
(f °g)(
a
 
 +
h
 
 ) - (f °g)(
a
 
 ) = f æ
è 		g(
a
 
 +
h
 
 ) ö
ø 		- f æ
è 		g(
a
 
 ) ö
ø 		= f æ
è 		g(
a
 
 ) +
k
 
 ö
ø 		- f æ
è 		g(
a
 
 ) ö
ø 		,
(13)
missä [`(k)] = g([`(a)]+ [`(h)]) - g([`(a)]). Kaikilla j = 1, ¼, n:
kj = gj(
a
 
 +
h
 
 ) - gj(
a
 
 ).
Koska gj on differentioituva
kj = D1 gj(
a
 
 )h1 + ¼+ Dn gj(
a
 
 )hm + ê
ê 		 
h
 
   ê
ê 		ej (
h
 
 ) = m
å
i = 1 
 Di gj (
a
 
 ) hi + ê
ê 		 
h
 
   ê
ê 		ej (
h
 
 ).
(14)
Toisaalta myös f on differentioituva pisteessä g([`(a)]), joten
f æ
è 		g(
a
 
 ) +
k
 
 ö
ø 		- f æ
è 		g(
a
 
 ) ö
ø
=
D1 f æ
è 		g(
a
 
 ) ö
ø 		k1 + ¼+ Dn f æ
è 		g(
a
 
 ) ö
ø 		kn + ê
ê 		 
k
 
   ê
ê
~
e
 
 (
k
 
 )
=
n
å
j = 1 
 (Dj f) æ
è 		g(
a
 
 ) ö
ø 		kj + ê
ê 		 
k
 
   ê
ê
~
e
 
 (
k
 
 ).
(15)
Yhdistämällä kaavat (13), (14) ja (15) saadaan
f °g (
a
 
 +
h
 
 ) - f °g(
a
 
 ) = m
å
i = 1 
 æ
è

n
å
j = 1 
 Dj f æ
è 		g(
a
 
 ) ö
ø 		Di gj (
a
 
 )
(*)
 
 
 ö
ø 		hi + h.
Pitkähkö tarkastelu osoittaa, että h®[`0] riittävän nopeasti, kun [`(h)]® 0 (tarkemmin sanoen [(h([`(h)]))/(| [`(h)] |)] ® 0 kun [`(h)]® 0). Tämän jälkeen Differentioituvuuden määritelmästä seuraa
(*) = Di(f °g)(
a
 
 ).

Esimerkki 7 Olkoon f(x, y) = x2y - y3. Laske funktion t ® f(2t3 - 5t, t4 + 3t + 7) derivaatta, kun t = -2.

Ratkaisu. Merkitään
h(t) = f(2t3 - 5t, t4 + 3t + 7) = f °g(t),
missä
g(t) = (2t3 - 5t, t4 + 3t + 7) = : æ
è 		g1(t), g2(t) ö
ø 		.
Lauseesta 3.5.2 seuraa
h¢(t) = D1 f æ
è 		g(t) ö
ø 		g¢1(t) + D2 f æ
è 		g(t) ö
ø 		g¢2(t).
Nyt
g1¢
=
6t2 - 5;
g2¢
=
4t3 + 3
D1 f(x, y)
=
2xy;
D2 f(x, y)
=
x2 - 3y2
g(-2)
=
(-6, 3)
D1 f(-6, 3)
=
-36 ;
D2 f(-6, 3)
=
9
g1¢(-2)
=
19;
g2¢(-2)
=
-29
Joten
h¢(-2) = -36 ·19 + 9 ·(-29) = -945.

Esimerkki 8 Olkoon f : R3 ® R differentioituva ja h : R2 ® R määritelty kaavalla
h(x, y) = f(x2 - y2, xy2, 2y);     x, y Î R.
Laske D1h ja D2h funktion f derivaattojen avulla.

Ratkaisu. Pätee h = f °g, missä
g(x, y) = (x2 - y2, xy2, 2y).
Ketjusääntö: (h:n osittaisderivaatta x:n suhteen i = 1 ketjusäännössä)
D1 h(x, y)
=
D1 f æ
è 		g(x, y) ö
ø 		D1 g1(x, y) + D2 f æ
è 		g(x, y) ö
ø 		D1 g2(x, y)
+ D3 f æ
è 		g(x, y) ö
ø 		D1 g3(x, y)
=
2x D1 f æ
è 		g(x, y) ö
ø 		+ y2 D2 f æ
è 		g(x, y) ö
ø 		.
Vastaavalla laskulla kun i = 2
D2 h(x, y) = -2y D1 f æ
è 		g(x, y) ö
ø 		+ 2xy D2 f æ
è 		g(x, y) ö
ø 		+ 2 D3 f æ
è 		g(x, y) ö
ø 		.

4  Käyrät, tasa-arvopinnat ja tangenttitaso

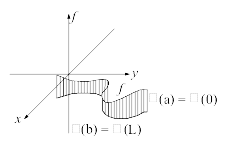
Määritelmä 9 Olkoon D Ì R väli (rajoitettu tai rajoittamaton) ja f : D® R2 jatkuva. Silloin joukko G: = f(D) on jatkuva käyrä. Yhtälöpari
ì
í
î
x
=
f1(t)
y
=
f2(t)
 ,     t Î D
on käyrän G parametriesitys, t parametri.

Esimerkki 10 Määritellään
f1(t)
=
2 + 3t
f2(t)
=
1 + 2t
 ,     t Î [ 0, 1 ] = : D.
Sillon G on jana, katso kuva 11. Jos
f1(t)
=
x1 + (x2 - x1)t
f2(t)
=
y1 + (y2 - y1)t,
niin G on jana, jonka päätepisteet ovat (x1, y1) ja (x2, y2).

kayrat1.png
Figure 11: jana G

Esimerkki 11 Määritellään
f1(t)
=
10 cost
f2(t)
=
10 sint
 ,     t Î [ 0, 2p]
Nyt G on ympyrä jonka keskipiste on [`0] ja säde 10.

Huomautus 12 Sanotaan, että G on rajoitettu, jos se sisältyy johonkin kiekkoon B(0, R) (jollekin R Î R+), muuten G on rajoittamaton.

Jos D on suljettu ja rajoitettu, niin f:n jatkuvuudesta seuraa, että G on rajoitettu. (Tämän asian todistus jätetään väliin.)

Esimerkki 13 Määritellään
f1(t)
=
t
f2(t)
=
 1
t
    ja     D = ] 0, 1 [
Katso kuva 12.

kayrat2.png
Figure 12: käyrä f(t) : = (t, [ 1/(t)])

Olkoon D = [ a, b ]. Jos f(a) = f(b), niin käyrä on umpinainen. Jos f on injektio, niin käyrää G sanotaan kaareksi.

Olkoon t: = [ a, b] ® [ a, b ] sellainen jatkuva surjektio, että t(a) = a ja t(b) = b. Silloin
G = g([ a, b]),
missä g : = f °t. Sanotaan, että käyrälle G on tehty parametrin vaihto.

Esimerkki 14 Määritellään
f1(t)
=
10cost
f2(t)
=
10sint
 ,     t Î [ 0, 2p].
ja
t: [ 0, 1 ] ® [ 0, 2p]        t(s) = 2ps.
Tällöin
g = f °t: [ 0, 1 ] ® R2
ja
g1(s)
=
10cos2ps
f2(s)
=
10sin2ps
 ,     s Î [ 0, 1 ].

Parametrin vaihto on sallittu muulloinkin kuin suljetun välin tapauksessa.

Vastaavasti määritellään avaruuskäyrät: Jos
f : D® R3
on jatkuva, niin käyrä G on joukko G = f(D). Edellä mainitut termit käyvät myös tässä.

Olkoon
ì
í
î
x
=
x(t)
y
=
y(t)

Määritelmä 15 Olkoon L pisteen f(s) kautta kulkeva suora, suuntavektori [`(a)]. Tällöin L on G:n tangentti pisteessä f(s), jos pisteiden f(s) ja f(r) kautta kulkevan suoran Lr suuntavektorille [`(b)](r) pätee:

lim
r ® s 
b
 
 (r) =
a
 
 .

Lause 16 Yllä olevassa tilanteessa
a
 
 = æ
è 		x¢(s), y¢(s) ö
ø 		,
(mikäli ainakin toinen komponenteista ¹ 0).

Todistus. 
b
 
 (r) ­­ æ
è 		x(r) - x(s), y(r) - y(s) ö
ø 		Þ
b
 
 (r) ­­ æ
è 		 x(r) - x(s)
r - s
 ,  y(r) - y(s)
r - s
 ö
ø 		,
ja viimeksi mainittu vektori lähestyy vektoria
æ
è 		x¢(s), y¢(s) ö
ø 		,
kun r ® s.     [¯]

R3:ssa [`(x)] on pisteen [`(x)]0 kautta kulkevan suoran S piste jos ja vain jos [`(x)] = t[`(a)] + [`(x)]0, missä [`(a)] ¹ 0 on suoran suuntavektori.

Avaruuskäyrän t ® [`(x)](t) tangentti(suora) määritellään kuten määritelmässä 4.0.15 ja pisteessä [`(x)](s) tangentti on vektorin
æ
è 		x1¢(s), x2¢(s), x3¢(s) ö
ø
suuntainen.

Esimerkki 17 Olkoon t Î [ 1, 10 ] ja [`(x)](t) : = (t, t2, t3). Kun t = 2, on tangentin suuntavektori
æ
è 		x1¢(2), x2¢(2), x3¢(2) ö
ø 		= (1, 4, 12).
Katso kuva 13.

kayrat4.png
Figure 13: Tangentin suuntavektori

Palataan tasokäyriin. Jatkuva käyrä esitetään usein muodossa
f(x, y) = 0,
missä piste (x, y) Î R2 kuuluu käyrälle ja funktio f on jossain A Ì R2 määritelty jatkuva funktio.

Esimerkki 18 Nollakeskeinen R-säteinen ympyrä tasossa:

Vastaavasti, jos f : A ® R, A Ì R2 jatkuva, niin joukko
ì
í
î 		(x, y) Î R2   ê
ê 		 f(x, y) = c ü
ý
þ
on käyrä, kun c Î R ja f toteuttaa tiettyjä ehtoja. Näitä käyriä sanotaan funktion f tasa-arvokäyriksi.

Osoitamme seuraavaksi, että funktion f gradientti on kohtisuorassa tasa-arvokäyrää vastaan:

Oletetaan, että c Î R on kiinteä ja että vastaavalla tasa-arvokäyrällä on parametriesitys
t ® æ
è 		x(t), y(t) ö
ø 		,    t Î D.
Oletetaan, että x(t) ja y(t) ovat derivoituvia. Koska
f æ
è 		x(t), y(t) ö
ø 		= c      " t Î D,
niin
0
=
df æ
è 		x(t), y(t) ö
ø
dt
=
(D1 f) æ
è 		x(t), y(t) ö
ø 		x¢(t) + (D2 f) æ
è 		x(t), y(t) ö
ø 		y¢(t)
=
(Ñf) æ
è 		x(t), y(t) ö
ø 		· æ
è 		x¢(t), y¢(t) ö
ø 		.
Näin ollen tangenttivektori on kohtisuorassa funktion f gradientti vektoria vastaan (jos x¢(0) ¹ 0 tai y¢(t) ¹ 0). Katso kuva 14.

kayrat5.png
Figure 14: Gradientti

4.1  Pinnat

Määritelmä 1 Avaruuden R3 suljettu osajoukko S on pinta, jos jokaisella [`(a)] Î S on ympäristö V joka on homeomorfinen neliön ] 0, 1 [ ×] 0, 1 [ (=: I2) kanssa. On olemassa jatkuva bijektio V ® I2.

Tarkastellaan nyt pintoja, jotka voidaan esittää muodossa
S : = ì
í
î 		(x, y, z)   ê
ê 		 f(x, y, z) = 0 ü
ý
þ 		,
missä f : A ® R jatkuva, A Ì R3.

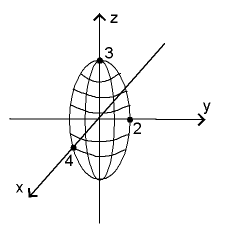
Esimerkki 2 Ellipsoidi


 x2
42
 +  y2
22
 +  z2
32
 - 1
=: f
 
 
 = 0.
Katso kuva 15.

pinnat1.png
Figure 15: Ellipsoidi

Esimerkki 3 Jos g : B ® R, B Ì R2, niin yhtälö
g(x, y) = z
määrittelee pinnan. Tämä voidaan näet kirjoittaa muodossa


g(x, y) - z
=: f 
 = 0.
Pinta on nimeltään g:n kuvaaja.

4.2  Tangenttitasot

Olkoon S pinta
{ f(x, y, z) = 0 }.
Olkoon (a, b, c) Î S pinnan piste. (Huom! f(a, b, c) = 0). Tarkoituksemme on johtaa tässä pisteessä olevan pinnan S tangenttitason yhtälö. Tarkastellaan käyrää G Ì S, joka kulkee pisteen (a, b, c) kautta. Oletetaan, että G:lla on derivoituva parametriesitys
t ® ì
ï
í
ï
î
x(t)
y(t)
z(t)
,     t Î D.
Olkoon t0 Î D sellainen piste, että
æ
è 		x(t0), y(t0), z(t0) ö
ø 		= (a, b, c).
Koska G Ì S, niin
f æ
è 		x(t), y(t), z(t) ö
ø 		= 0  " t Î D,
ja tästä saadaan
0
=
d f æ
è 		x(t), y(t), z(t) ö
ø
dt
=
(D1t) æ
è 		x(t), y(t), z(t) ö
ø 		x¢(t) + (D2t) æ
è 		x(t), y(t), z(t) ö
ø 		y¢(t)
+ (D3t) æ
è 		x(t), y(t), z(t) ö
ø 		z¢(t)
=
(Ñf) æ
è 		x(t), y(t), z(t) ö
ø 		· æ
è 		x¢(t), y¢(t), z¢(t) ö
ø 		.
Kun t = t0, saadaan
(Ñf) (a, b, c) · æ
è 		x¢(t), y¢(t), z¢(t) ö
ø 		= 0
joten kaikkien yllä mainittujen käyrien tangentit ovat kohtisuorassa gradienttia (Ñf) (a, b, c) vastaan.

Tangenttitason yhtälö

Merkitään
r
 
0 
 : = (a, b, c) = a
i
 
 + b
j
 
 + c
k
 
 .
Olkoon [`(r)] = (x, y, z) tangenttitason T piste. Siis
(x, y, z) Î T
Û
r
 
 -
r
 
0 
 ^Ñf(a, b, c)
Û
Ñf(a, b, c) ·(
r
 
 -
r
 
0 
 ) = 0
Û
D1 f(a, b, c) (x - a) + D2 f(a, b, c) (y - b)+ D3 f(a, b, c) (z - c) = 0.
Tämä on T:n yhtälö.

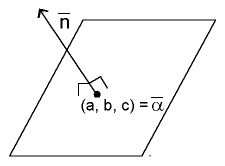
Esimerkki 1 Määritellään pinta
 x2
42
 +  y2
22
 +  x2
32
 - 1 = 0.
Haluamme muodostaa tangenttitason yhtälön pisteessä (a, b, c) = (2, 1, [ 3/(Ö2)]).
(Ñf) (x, y, z)
=
æ
è 		 x
8
 ,  y
2
 ,  2z
9
 ö
ø
(Ñf) (2, 1,  3
Ö2
 )
=
æ
è 		 1
4
 ,  1
2
 ,  Ö2
3
 ö
ø 		.
T:n yhtälö
 1
4
 (x - 2) +  1
2
 (y - 1)+  Ö2
3
 æ
è 		z -  3
Ö2
 ö
ø 		= 0
eli
 x
4
 +  y
2
 +  Ö2
3
 z -2 = 0.

Esimerkki 2 Olkoon g : A ® R, A Î R2, g differentioituva. Tarkastellaan pintaa S, joka on funktion g kuvaaja,
S = { (x, y, z)   ê
ê 		 

g(x, y) - z
=: f(x, y, z) 
 = 0 }
Nyt
(Ñf)(a, b, c) = æ
è 		(D1 g)(a, b), (D2 g)(a, b), -1 ö
ø 		.
Pisteen ( a, b, g(a, b) ) kautta kulkevan tangenttitason yhtälö on näin ollen
D1 g(a, b) (x - a) + D2 g(a, b)(b - y) = z - c.

Tason T yhtälö R3:ssa yleisesti

ttaso1.png
Figure 16: Taso T

T:n määrää:

Oletetaan että nämä annettu: Olkoon [`(x)] Î R3 mielivaltainen tason T piste. Silloin [`(x)] toteuttaa yhtälön:
(
x
 
 -
a
 
 ) ·
n
 
 = 0
eli
x1 n1 + x2 n2 + x3 n3 - Î R
a
 
 ·
n
 


 
 = 0.
Yleisesti siis tason yhtälö on muotoa
Ax + By + Cz + D = 0,
missä A, B, C, D Î R.

Esimerkki 3 Määritellään [`(a)] = (2, 2, 1) ja [`(n)] = [`(k)] = (0, 0, 1). Nyt n1 = n2 = 0, [`(a)] ·[`(n)] = 1. Yhtälö:
z = 1.
(Piste (x, y, z) kuuluu tasoon, jos ja vain jos z = 1).

Suoran yhtälö R3:ssa

Pisteen [`(a)] kautta kulkevan, vektorin [`(b)] suuntaisen suoran L yhtälö on
x
 
 = t
b
 
 +
a
 
 ,     t Î R.
(16)
Toisin sanoen, [`(x)] Î L jos ja vain jos on olemassa luku t siten, että (16) toteutuu.

Voidaan kirjoittaa myös muodossa
 x1 - a1
c1
 =  x2 - a2
c2
 =  x3 - a3
c3
jollekin cj Î R.

5  Väliarvolause

Lause 4 Olkoon A Ì °  R2 ja f : A ® R differentioituva, ja olkoot [`(a)], [`(b)] Î A sellaisia pisteitä, että niiden yhdysjana sisältyy A:han. Tällöin on olemassa q Î [ 0, 1 ], jolle
f(
b
 
 ) - f(
a
 
 ) = Ñf æ
è
a
 
 + q(
b
 
 -
a
 
 ) ö
ø 		·(
b
 
 -
a
 
 ).
(17)

Huomautus 5 1) Lause 5.0.4 pätee, kun R2 muutetaan Rn:ksi.

2) Jos merkitään [`(b)]- [`(a)] = [`(h)], niin (17) pätee jos ja vain jos
f(
a
 
 -
h
 
 ) - f(
a
 
 ) = Ñf(
a
 
 + q
h
 
 ) ·
h
 
 .

Lauseen 5.0.4 todistus:

Todistus.  Olkoon pisteiden [`(a)] ja [`(b)] yhdysjana
J = {
a
 
 + th   ê
ê 		 0 £ t £ 1 }.
Määritellään derivoituva funktio g : [ 0, 1 ] ® R,
g(t) = f(
a
 
 + t
h
 
 )     æ
è 		=f(
a
 
 + t(
b
 
 -
a
 
 ) ö
ø 		.
Ketjusäännön mukaan
g¢(t) = D1f(
a
 
 + t
h
 
 )h1 + D2(
a
 
 + t
h
 
 )h2 = Ñf(
a
 
 + t
h
 
 ) ·
h
 
 .
Toisaalta väliarvolauseesta seuraa, että on olemassa q Î ] 0, 1 [, jolle
g(1) - g(0) = g¢(q)(1 - 0) = g¢(q).
Saamme
f(
a
 
 +
h
 
 ) - f(
a
 
 ) = g(1) - g(0) = g¢(q) = Ñf(
a
 
 + q
h
 
 ) ·
h
 
 .
    [¯]

Esimerkki 6 Jos | Ñf([`(a)]) | £ M tarkastelualueessa (ainakin janalla J), missä M on jokin positiivinen vakio, niin
ê
ê 		 f(
b
 
 ) - f(
a
 
 )  ê
ê
=
ê
ê 		 Ñf(
a
 
 + q(
b
 
 -
a
 
 ) ) ·(
b
 
 -
a
 
 )  ê
ê
£
ê
ê 		 Ñf(a + q(
b
 
 -
a
 
 ) )  ê
ê 		ê
ê 		 
b
 
 -
a
 
   ê
ê
£
M ê
ê 		 
b
 
 -
a
 
   ê
ê 		.
Kaavaa voidaan soveltaa fysiikan virhearvioinneissa: [`(b)] on jokin mitattu suure, [`(a)] sen tarkka arvo, | [`(b)]- [`(a)] | mittausvirhe (josta on jonkinlainen käsitys olemassa). Lauseke f([`(a)]) on etsitty suure, ja edellä mainitun kaavan mukaan M| [`(b)]- [`(a)] | on yläraja arvio virheelle, joka tehdään, kun f([`(a)]):n likiarvo f([`(b)]) lasketaan mittaustuloksen [`(b)] perusteella.

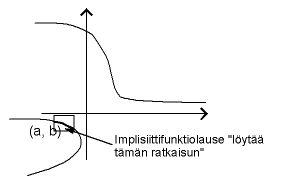
5.1  Implisiittifunktiolause

Lause 1 Olkoon A Ì °  R2 ja f: A ® R jatkuvasti derivoituva. Olkoon (a, b) piste, joka on f:n nollakohta, f(a, b) = 0. Oletetaan, että D2 f(a, b) ¹ 0. Tällöin on olemassa sellainen suorakulmio
D = { (x, y)   ê
ê 		 a1 < x < a2, b1 < y < b2 } Ì R2,
(a, b) Î D, että jokaista x Î ] a1, a2 [ kohti yhtälöllä
f(x, y) = 0
on yksikäsitteinen ratkaisu y(x) Î ] b1, b2 [. Funktio x ® y(x) on jakuvasti derivoituva välillä ] a1, a2 [.

Huomautus. Siis funktio x ® y(x) toteuttaa f(x, y(x)) = 0,  " x Î ] a1, a2 [. Katso kuva 17.

impli1.png
Figure 17: Suorakulmio D

Esimerkki 2 Funktion
f(x, y) = y5 + xy - 4 = 0
ratkaisupisteet tasossa: Katso kuva 18.

impli2.png
Figure 18: Ratkaisupisteet

Yhtälön koko ratkaisu ei ole minkään yhden muuttujan funktion kuvaaja!

Lauseen 5.1.1 todistus.

Todistus.  Oletetaan että D2 f(a, b) > 0. Koska D2f on jatkuva, tästä seuraa että on olemassa r > 0 siten, että D2 f(x, y) > 0, kun (x, y) Î B([`(a)], r) (tässä [`(a)] : = (a, b)). Tarkastellaan funktioita y ® f(a, y); yllä olevan nojalla se on aidosti kasvava b:n n-ympäristössä. Olkoon b1, b2 Î R sellaisia, että
b -  r
2
 < b1 < b < b2 < b +  r
2
 .
Tällöin
f(a, b1) < 0 = f(a, b) < f(a, b2).
Koska f jatkuva, niin on olemassa sellaiset luvut a1, a2,
a -  r
2
 < a1 < a < a2 < a +  r
2
 ,
että
f(x, b1) < 0,     f(x, b2) > 0,
kun a1 < x < a2. Olkoon x Î ] a1, a2 [. Nyt pätee

Tästä seuraa, että on olemassa y = y(x) Î ] b1, b2 [, jolle j(y(x)) = 0 eli f(x, y(x)) = 0. Todistus sille, että y(x) on derivoituva, sivuutetaan.     [¯]

Olkoon f: A ® R, A Ì °  R2, f(a, b) = 0 ja D2 f(a, b) ¹ 0. Implisiittifunktiolauseesta siis seuraa, että yhtälöllä f(x, y) = 0 on yksikäsitteinen ratkaisu y(x) jokaista x Î ] a1, a2 [ kohti. Funktio x ® y(x) on jatkuvasti derivoituva. Derivaatan y¢(x) laskeminen:

Pätee f(x, y(x) ) = 0, joten
0 =  d
dx
 f(x, y(x) ) = D1 f(x, y(x) ) ·1 +(D2 f)(x, y(x)) ·y¢(x)
mistä seuraa
y¢(x) =  -D1 f(a, b)
D2 f(a, b)
 .

Esimerkki 3 Tarkastellaan yhtälöä
xy - sin(x + y) = 0
(18)
Tällä on ratkaisu x = y = 0. Osoitetaan, että kyseessä oleva yhtälö määrittelee y:n x:n funktiona jossakin pisteen nolla ympäristössä ja lasketaan y¢(0).

Ratkaisu. Pätee f(0, 0) = 0 (Lause 5.1.1 kun a = 0, b = 0) ja D2 f(x, y) = x - cos(x + y), D2 f(0, 0) = -1 ¹ 0. Lause 5.1.1 soveltuu, joten yhtälö (18) määritteöee y:n x:n funktiona.
y¢(0) =  D1 f(0, 0)
D2 f(0, 0)
 =  -1
1
 = -1.
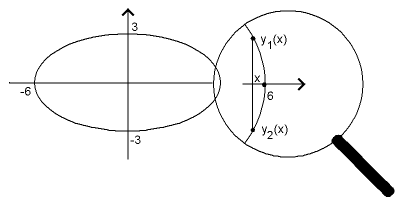
ja
D1 f = y - cos(x + y).

Tapaus, jossa implisiittilause EI toimi:

Tarkastellaan yhtälöä
æ
è 		 x
2
 ö
ø 		2

 
 + y2 - 9 = 0
(19)
pisteessä (x, y) = (6, 0). Nyt
D2 f(x, y) = 2y,     D2 f(6, 0) = 0,
joten implisiittifunktiolauseen oletukset eivät ole voimassa.

Huomautus 4 Yhtälön (19) ratkaisupisteet muodostavat ellipsin tasoon. Katso kuva 19. Eli y ei ole yksikäsitteinen x:n funktio.

impli3.png
Figure 19: Ellipsi

Lause 5 Olkoon A Ì °  Rn + 1 ja f: A ® R jatkuvasti derivoituva funktio, jolle pisteessä ([`(a)], b) Î A Ì Rn + 1
f(
a
 
 , b) = 0,     Dn + 1 (
a
 
 , b) ¹ 0.
Tällöin on olemassa [`(a)]:n ympäristö B([`(a)], r) Ì Rn ja avoin väli ] b1, b2 [ ' b siten, että jokaisella [`(x)] Î B([`(a)], r) yhtälöllä f([`(x)], y) = 0 on yksikäsitteinen ratkaisu y([`(x)]) Î ] b1, b2 [.

Derivaatoille pätee:
Di y(
x
 
 ) = -
Di f(
x
 
 , y(
x
 
 ))
Dn + 1f(
x
 
 , y(
x
 
 ))
     i = 1, ¼, n.
Lausetta 5.1.5 voidaan käyttää, kun halutaan varmistaa, että yhtälön f(x, y, z) = 0 ratkaisut muodostavat pinnan R3:ssa (vertaa luku 4).

Esimerkki 6 Yhtälö
f(x, y, z) = zex2 + y2 + z2 = 0
määrittelee z:n muuttujien x ja y funktiona eräässä (0, 0, 0):n ympäristössä, sillä
f(0, 0, 0) = 0 ·e0 = 0,
eli yhtälö toteutuu. Nyt
D3 f(x, y, z)
=
ex2 + y2 + z2 + z ·2zex2 + y2 + z2
D3 f(0, 0, 0)
=
1 ¹ 0
D1 f(x, y, z)
=
2xzex2 + y2 + z2.
Siis voidaan ratkaista z = z(x, y), kun (x, y) on pisteen (0, 0) jossain ympäristössä. Derivaatalle saadaan
 z
x
 (0, 0) = D1 z(0, 0) = -  D1 f(0, 0, 0)
D3 f(0, 0, 0)
 = -  0
1
 = 0.

6  Ääriarvojen teoriaa

Tutkitaan aluksi neliömuotoja kahden muuttujan x, y tapauksessa:
P(x, y) = ax2 + 2bxy + cx2,
(20)
missä a, b, c Î R annettuja kertoimia.

Esimerkki 7 Määritellään
P(x, y) = 2x2 - 10xy + 3y2.
Nähdään että P(0, 0) = 0

  1. Jos P(x, y) ¹ 0 aina, kun (x, y) ¹ (0, 0), niin P on definiitti.

      a) Jos P(x, y) > 0 aina, kun (x, y) = (0, 0), niin P on positiivisesti definiitti.
      b) Jos P(x, y) < 0 aina, kun (x, y) = (0, 0), niin P on negatiivisesti definiitti.

  2. Jos P(x, y) ³ 0  " (x, y) Î R2 tai jos P(x, y) £ 0  " (x, y) Î R2, niin P on semidefiniitti. (Huomautus! Jos P on definiitti, on se myös semidefiniitti.)

  3. Jos P saa positiivisia ja negatiivisia arvoja, se on indefiniitti.

Yleisemmin, neliömuoto Rn:ssä on muotoa
P(
x
 
 ) =
x
 
 T
 
 A
x
 
 = n
å
i = 1 
 aiixi2 +
å
1 £ i < j £ n 
 2aijxi xj,
missä A on n ×n matriisi (aij)i, j = 1n.

Lause 8 Neliömuoto (20) on

Merkitään D : = ac - b2.

Todistus.  Oletetaan, että D > 0. Silloin a ¹ 0 ja P(x, y) voidaan kirjoittaa muodossa
P(x, y) =  1
a
 [ (ax + by)2 + Dy2 ].
Jos P(x, y) = 0, niin
0 = aP(x, y) = (ax + by)2 + Dy2.
Tämä on mahdollista vain jos Dy2 = 0 ja (ax + by)2 = 0 eli y = 0 ja (ax + 0)2 = 0 eli y = 0 ja x = 0 (koska a ¹ 0).

Oletetaan nyt D < 0 ja a ¹ 0. Tällöin
P(x, y) =  1
a
 æ
è 		(ax + by)2 + Dy2 ö
ø 		=  1
a
 æ
è 		(ax + by) -
Ö
 
| D |
 
 y ö
ø 		æ
è 		(ax + by) +
Ö
 
| D |
 
 y ö
ø 		.
Nähdään, että P häviää xy-tason suorilla
ax + (b -
Ö
 
| D |
 
 )y = 0 ja ax + (b +
Ö
 
| D |
 
 )y = 0.
Siis P on indefiniitti.

Tapaus a = 0, D < 0. Tällöin
P(x, y) = y(2bx + cy).
Koska D = ac - b2 < 0 ja a = 0, niin täytyy olla b ¹ 0. Otetaan y = 1:
P(x, 1) = 2bx + c,
joka saa negatiivisia ja positiivisia arvoja kun x Î R. P on siis indefiniitti.

Tapaus D = 0.

  1. Jos a ¹ 0, niin P(x, y) = [ 1/(a)](ax + by)2,

  2. Jos a = 0, niin P(x, y) = cy2 Þ b = 0.
Selvästikin P on semidefiniitti.     [¯]

Esimerkki 9 Määritellään
P(x, y) = x2 - 6xy + 2y2.
Nyt a = 1, b = -3, c = 2 ja D = 2 - 9 = -7, eli P on indefiniitti. P(x, y) häviää suorilla
y = æ
è 		 1
3 ±Ö7
 ö
ø 		x.
Esimerkiksi
P(1, 1)
=
1 - 6 + 2 = -3 < 0
P(1, -1)
=
1 + 6 + 2 = 9 > 0.

Esimerkki 10 Määritellään
P(x, y) = 4xy - 4x2 - y2.
Nyt a = -4, b = 2, c = -1 ja D = 4 - 4 = 0 (semidefiniitti). Itseasiassa P(x, y) = -(2x - y)2, mistä nähdään

Esimerkki 11 Määritellään
P(x, y) = 2xy - 3x2 - y2.
Nyt a = -3, b = 1, c = -1 ja D = 2 > 0 (definiitti). Esimerkiksi P(1, 1) = -2 < 0. Siis P(x, y) < 0, kun (x, y) ¹ [`0].

6.1  Taylorin kaava

Olkoon A Ì °  R2, f : A ® R funktio, jolla on kaikkien kertalukujen jatkuvat osittaisderivaatat. Olkoon [`(x)] Î A tarkastelupiste ja [`(h)] Î R2 siten, että jana
J : = {
x
 
 + t
h
 
   ê
ê 		 t Î [ 0, 1 ] } Ì A.
J on jana, jonka päätepisteet ovat [`(x)] ja [`(x)]+ [`(h)]. Määritellään
g
:
[ 0, 1 ] ® A
g(t)
=
x
 
 + t
h
 
g(0)
=
x
 
g(1)
=
x
 
 +
h
 
 .
Tarkastellaan funktiota
f °g : [ 0, 1 ] ® R,
joka on mielivaltaisen monta kertaa derivoituva yhden muuttujan funktio.

Ketjusäännön mukaan
(f °g)¢ = (D1 f) °g ·g1¢+ (D2 f) °g2¢ = h1 (D1 f) °g + h2 (D2 h) °g.

Huomautus 1
g(t) = æ
è 		g1(t), g2(t) ö
ø 		= (x1 + th1, x2 + th2),
missä [`(x)] = (x1, x2), [`(h)] = (h1, h2) ja g1¢ = h1, g2¢ = h2. Edelleen
(f °g)¢¢
=
h1  d
dt
 (D1 f °g) + h2  d
dt
 (D2 f °g)
=
h1 æ
è 		h1 (D11 f) °g + h2 (D12 f) °g ö
ø 		+ h2 æ
è 		h1 (D21 f) °g + h2 (D22 f) °g ö
ø
=
h12 (D11 f) °g + 2h1 h2 (D12 f) °g + h22 (D22 f) °g
=
æ
è 		(h1D1 + h2D2)2 f ö
ø 		°g,
missä D12 = D11, D1D2 = D12 = D2D1 ja D22 = D22. Induktiolla voidaan todistaa kaava
(f °g)(k) = æ
è 		(n1 D1 + h2 D2)k f ö
ø 		°g.

Taylorin kaavasta yhden muuttujan funktiolle F : B ® R, missä [ 0, 1 ] Ì B Ì °  R, saadaan
F(1) = n - 1
å
k = 0 
  1
k!
 F(k)(0) +  1
n!
 F(n)(q),
(21)
missä q Î ] 0, 1 [ (jos n = 1, tämä on väliarvolause).

Jos F toteuttaa tietyt (ankarat) vaatimukset, sille pätee kehitelmä
F(x) = ¥
å
k = 0 
  1
k!
 F(k)(0)xk,
missä x Î B(0, r).

Taylorin kehitelmä (21) pätee funktiolle F, jos se on n kertaa jatkuvasti derivoituva. Sovelletaan tätä, kun F : = f °g:
(f °g)(1) = n - 1
å
k = 0 
  (f °g)(k)(0)
k!
 +  (f °g)(n)(q)
n!
 .
Sijoittamalla k:nen derivaatan lauseke ja ottamalla huomioon
g(0) =
x
 
 ,     g(1) =
x
 
 +
h
 
 ,     g(q) =
x
 
 + q
h
 
 ,
saadaan
f(
x
 
 +
h
 
 )
=
f(g(1)) = f °g (1)
=
n - 1
å
k = 0 
  1
k!
 (h1D1 + h2D2)k f(
x
 
 ) +  1
n!
 (h1D1 + h2D2)n f(
x
 
 + q
h
 
 ),
missä q Î ] 0, 1 [. Tämä kehitelmä pätee, kun f on n kertaa jatkuvasti derivoituva. Arvolla n = 2 kehitelmästä seuraa

Lause 2 Olkoon f: A ® R, A Ì °  R2, kaksi kertaa jatkuvasti derivoituva. Olkoon [`(x)] Î A, [`(h)] Î R2 ja [`(h)] Î B([`0], r), missä r on niin pieni, etä [`(x)]+ B([`0], r) Ì A. Tällöin
f(
x
 
 +
h
 
 ) - f(
x
 
 )
=
h1D1f(
x
 
 ) + h2D2f(
x
 
 )
+  1
2
 æ
è 		h12 D11 f(
x
 
 ) + 2h1h2 D12 f(
x
 
 ) + h22 D22 f(
x
 
 ) ö
ø
+ ê
ê 		 
h
 
   ê
ê 		2
 
 e(h),
missä e([`(h)]) ® 0, kun [`(h)]®[`0].

6.2  Ääriarvoista

Olkoon f: A ® R, A Ì °  Rm, m Î N. Tällöin

Lause 1 Olkoon f: A ® R, A Ì °  Rm, kerran derivoituva. Jos [`(a)] Î A on f:n ääriarvopiste, niin Di f([`(a)]) = 0, kun i = 1, ¼, m.

Esimerkki 2 Määritellään
f(x, y) = x2 + y2.
Nyt
D1 f(x, y)
=
2x
D2 f(x, y)
=
2y
Dj f(0, 0)
=
0,     kun j = 1, 2
Tunnetusti f:llä on lokaali minimi pisteessä [`0].

Esimerkki 3 Määritellään
f(x, y) = x2 - y2.
Nyt pätee D1 f(0, 0) = 0 = D2 f(0, 0). Toisaalta (0, 0) ei ole ääriarvopiste:
f(0, r)
=
-r2 < 0
f(r, 0)
=
r2 > 0

Lauseen 6.2.1 todistus:

Todistus.  Tehdään antiteesi: Oletetaan että [`(a)] Î A on A:n ääripiste ja Dk f([`(a)]) ¹ 0, jollekin k Î {1, ¼, m}. Määritellään funktio
g(x) = f(a1, ¼, ak - 1, x, ak + 1, ¼, am)
(22)
missä x Î B(ak, r) Ì R jollakin r > 0.

Nyt
 dg
dx
 (ak) = Dk f(
a
 
 ) ¹ 0.
Näin ollen g saa ak:n ympäristössä sekä suurempia että pienempiä arvoja kuin g(ak). Kohdan 22 nojalla sama pätee funktiolle f, joten [`(a)] ei ole funktion f ääriarvopiste.     [¯]

Lause 4 Olkoon A Ì °  R2, f: A ® R. Oletetaan että funktiolla f on jatkuvat kertaluvun 1. ja 2. osittaisderivaatat. Jos pisteessä [`(a)] Î A pätee
D1 f(
a
 
 ) = 0 = D2 f(
a
 
 )
ja
D : = D11f(
a
 
 ) D22f(
a
 
 ) - D12(
a
 
 )2 > 0,
(23)
niin [`(a)] on oleellinen ääriarvopiste;

Määritelmä 5 Satulapiste. Olkoon A, [`(a)], f kuten lauseen 6.4 oletuksessa.
D1 f(
a
 
 ) = D2 f(
a
 
 ) = 0.
Jos f saa [`(a)]:n mielivaltaisessa ympäristössä sekä suurempia että pienempiä arvoja kuin f([`(a)]), niin [`(a)] on satulapiste.

Esimerkki 6 Määritellään
f(x, y) = x2 - y2.
Derivaatat ovat
D1
=
2x
D2
=
-2y
D11
=
2
D22
=
-2
D12
=
0
joten
D1 f(x, y) = 0
Û
2x = 0
Û
x = 0
D2 f(x, y) = 0
Û
-2y = 0
Û
y = 0.
Pisteessä [`(a)] = (0, 0)
D11 f(
a
 
 ) D22 f(
a
 
 ) - D12 f(
a
 
 )2 < 0.

Esimerkki 7 Määritellään
f(x, y) = x2 + xy + y2 + x - y.
Tehtävänä on etsiä ääriarvo- ja satulapisteet.

Ratkaisu. Osittaisderivaatat
D1 f
=
2x + y + 1
D2 f
=
x + 2y - 1.
Jos (x, y) on kriittinen piste (eli derivaattojen nollakohta), niin
ì
í
î
2x
+
y
+
1
=
0
x
+
2y
-
1
=
0
Þ ì
í
î
y
=
1
x
=
-1.
Pisteessä (-1, 1) pätee
D11
=
2
D22
=
2
D12
=
1
ü
ï
ý
ï
þ 		Þ D(-1, 1) > 0,
eli kyseessä on ääriarvopiste (minimi).

Esimerkki 8 Määritellään
f(x, y) = x3 - y3 + 3xy.
Derivaatat ovat
D1 f
=
3x2 + 3y
D2 f
=
-3y2 + 3x.
Kriittiset pisteet ovat
ì
í
î
3x2
+
3y
=
0
-3y2
+
3x
=
0
Û
ì
í
î
x
=
x4
y
=
-x2
Û
(x, y) = (0, 0) tai (x, y) = (1, -1).
Edelleen
D11 f = 6x,     D22 f = -6y,     D12 f = 3,
joten
D(0, 0)
=
-9 < 0    (satulapiste eli ei ääriarvopiste)
D(-1, 1)
=
6 ·1 ·(-6) ·(-1) - 9 = 36 - 9 > 0    (minimi.)

Lauseen 6.2.4 todistuksesta:

Olkoon [`(h)] Î B(0, r), r > 0. Lauseen 6.1.2 mukaan pätee
f(
a
 
 +
h
 
 ) - f(
a
 
 )
=
D1f(
a
 
 )h1 + D2f(
a
 
 )h2
+  1
2
 æ
è 		D11 f(
a
 
 )h12 + 2D12 f(
a
 
 )h1h2
+ D22 f(
a
 
 )h22 ö
ø 		+ ê
ê 		 
h
 
   ê
ê 		e(
h
 
 ),
missä e([`(h)]) ® 0, kun [`(h)]® 0. Koska [`(h)] on pieni ja D1f([`(a)]) = D2f([`(a)]) = 0, määrää lauseke
D11 f(
a
 
 )h12 + 2D12 f(
a
 
 )h1h2 + D22 f(
a
 
 )h22
(24)
erotuksen f([`(a)]+ [`(h)]) - f([`(a)]) etumerkin. Lauseke (24) on neliömuoto P(h1, h2), kertoimet a = D11 f([`(a)]), b = D12 f([`(a)]), c = D22 f([`(a)]). Ylläolevista määritelmistä seuraa, että [`(a)] on ääriarvopiste jos ja vain jos neliömuoto P on definiitti. Huomaa, että
D > 0 Û D(
a
 
 ) > 0.
Yllä olevat tarkastelut olivat lokaaleja.

Esimerkki 9 Funktion suurin tai pienin arvo joukossa B Ì R2. Olkoon B kompakti (eli rajoitettu ja suljettu). Nyt pätee: Jos f: B ® R on jatkuva, niin f saa B:ssä suurimman ja pienimmän arvon. Esimerkiksi jos C : = [ 0, ¥[, niin funktio f(x) = [ 1/(x)] ei saa joukossa C pienintä arvoaan. Mutta C ei olekaan kompakti joukko.

Huomautus 10 Se, että funktio f: B ® R saa pienimmän arvonsa pisteessä [`(x)]0 Î B, tarkoittaa, että
f(
y
 
 ) ³ f(
x
 
0 
 )  " y Î B.

Olkoon B kompakti, f: B ® R jatkuva ja kaksi kertaa jatkuvasti derivoituva. Ainoat pisteet, joissa f voi saada suurimman tai pienimmän arvonsa ovat

  1. f:n lokaalit ääriarvopisteet

  2. B:n reunapisteet.

Yllä esitettyä lokaalien ääriarvojen tarkastelua voidaan siten käyttää hyväksi myös globaalien ääriarvojen eli suurimman ja pienimmän arvon löytämiseksi. Lopuksi, ilman todistuksia esitetään n:n muuttujan funktioiden ääriarvojen teoriaa.

Lause 11 Olkoon n Î N, n ³ 2, A Ì °  Rn, f: A ® R derivoituva. Jos funktiolla f on ääriarvo pisteessä [`(a)] Î A, niin
Ñf(
a
 
 ) = 0     eli    D1 f(
a
 
 ) = D2 f(
a
 
 ) = ¼ = Dn f(
a
 
 ) = 0.

Todistus.  Sama kuin n = 2.     [¯]

Lause 12 Olkoon A Ì °  Rn, f kaksi kertaa jatkuvasti derivoituva ja
Ñf(
a
 
 ) = 0 pisteessä
a
 
 Î A.
Muodostetaan funktion f Hessen matriisi
H =   æ
ç
ç
ç
ç
ç
ç
ç
ç
ç
ç
è
D11f(
a
 
 )
D12f(
a
 
 )
¼
D1nf(
a
 
 )
D21f(
a
 
 )
D22f(
a
 
 )
¼
D2nf(
a
 
 )
:
···
Dn1f(
a
 
 )
Dn2f(
a
 
 )
¼
Dnnf(
a
 
 )
ö
÷
÷
÷
÷
÷
÷
÷
÷
÷
÷
ø 		 
ja diagonalisoidaan se; saadaan muotoa
  æ
ç
ç
ç
ç
ç
è
l1
0
¼
0
0
l2
:
:
···
0
¼
ln
 ö
÷
÷
÷
÷
÷
ø 		 
oleva matriisi. Seuraavat tulokset pätevät:

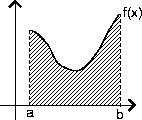
7  Käyräintegraalit

Olkoon f: [ a, b ] ® R jatkuva. Sen integraalifunktiota F : [ a, b ] ® R merkitään
F(x) : = x
ó
õ
a 
 f(t) dt,
ja sille pätee kaava [(dF)/(dx)] = f. Geometrinen tulkinta:

ala.png
Figure 20: Pinta-ala

Kuvan 20 väritetyn alueen pinta-ala on òab f(x) dx.

Olkoon j: [ a, b ] ® R2 (tai Rn) jatkuva. Joukko j([ a, b ]) Ì R2 on käyrä, jota merkitään esimerkiksi G. Kuvaus j on G:n parametriesitys.

Jos käyrällä on parametriesitys, joka on injektio, sitä sanotaan kaareksi. Valitsemalla toinen päätepiste alkupisteeksi ja toinen loppupisteeksi, saadaan suunnistettu kaari. Kaari on säännöllinen, jos sillä on jatkuvasti derivoituva parametriesitys.

Määritelmä 13 Olkoon G Ì R2 säännöllinen suunnistettu kaari ja olkoon j = (j1, j2) jatkuvasti derivoituva parametriesitys (siis G = j([ a, b ])). Jos f: G® R ja g: G® R ovat jatkuvia, niin määritellään

ó
õ
G 
 f dx + g dy : = b
ó
õ
a 
 æ
è 		f(j(t)) j1¢(t) +g(j(t)) j2¢(t) ö
ø 		 dt.

Yleisesti:
G Ì Rn,     g: [ a, b ] ® Rn,    g([ a, b ]) = G,     g = (g1, ¼, gn)
jatkuvasti derivoituva. Olkoon fj : G® R, j = 1, 2, ¼, n. Määritellään

ó
õ
G 
 f1 dx1 + f2 dx2 + ¼+ fn dxn: = b
ó
õ
a 
 æ
è 		f1(g(t))g1¢+ ¼+ fn(g(t))gn¢(t) ö
ø 		 dt
Merkitään myös

ó
õ
G 
 f1 dx1 + f2 dx2 + ¼+ fn dxn: =
ó
õ
G 
f
 
 ·d
r
 
 ,
missä [`]f : = (f1, ¼, fn) ja d[`(r)] : = (dx1, ¼, dxn).

Lause 14 Määritelmän 7.0.13 käyräintegraali ei riipu G:n parametriesityksestä.

Todistus.  Sivuutetaan.     [¯]

Esimerkki 15 Laske

ó
õ
G 
 x2 dx + xy dy,
kun G on yksikköympyrän kaari pisteestä (1, 0) pisteeseen (0, 1).

Ratkaisu. Käytetään G:lle tuttua parametrisointia
ì
í
î
x = j1(t) = cost
y = j2(t) = sint
,    0 £ t £  p
2
 .
Tällöin
j1¢(t)
=
-sint,
j2¢(t)
=
cost
dx
=
j1¢(t) dt,
dy
=
j2¢(t) dt
ja

ó
õ
G 
 x2 dx + xy dy = p/2
ó
õ
0 
 æ
è 		cos2 t ·(-sint) + cost sint cost ö
ø 		 dt = 0.
Toinen mahdollisuus on käyttää G:lle parametriesitystä
ì
ï
í
ï
î
x
=
-t
y
=

Ö
 
1 - t2
 
,     t Î [ -1, 0 ].
Tällöin j: [ -1, 0 ] ® R2 ja
j(t) = æ
è 		j1(t), j2(t) ö
ø 		= (-t,
Ö
 
1 - t2
 
 ).
Huomaa, että

Ö
 
x(t)2 + y(t)2
 
 =
Ö
 
t2 + (1 - t2)
 
 = 1.

Tällä parametriesityksellä

ó
õ
G 
 x2 dx + xy dy = 0
ó
õ
-1 
 æ
ç
è 		t2 ·(-1) + (-t)
Ö
 
1 - t2
 
 ·  -t

Ö
1 - t2
 ö
÷
ø 		dt = 0
ó
õ
-1 
 (-t2 + t2) dt = 0,
sillä j1¢(t) = -1 ja
j2¢(t) =  1
2
 (1 - t)-[ 1/2] ·(-2t) =  -t

Ö
1 - t2
Käyräintegraalin käsite liittyy läheisesti fysiikkaan.

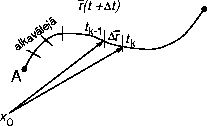
Esimerkki 16 Tarkastellaan massapistettä, joka liikkuu pitkin R3:n käyrää G. Kappaleeseen vaikuttaa voima
F
 
 (x, y, z) = F1(x, y, z)
i
 
 + F2(x, y, z)
j
 
 + F3(x, y, z)
k
 
missä [`(F)] : R3 ® R3, [`(F)] = (F1, F2, F3).

Ratkaisu. Massapisteen sijainti ajan t funktiona (aikaväli on a £ t £ b) on
r
 
 (t) = (x(t), y(t), z(t)) = x(t)
i
 
 + y(t)
j
 
 + z(t)
k
 
 ,
katso kuva 21.

massakayra.png
Figure 21: Massapisteen sijainti

Kun aika muuttuu (vähän) hetkestä t hetkeen t + Dt, massapisteen paikan muutos on
D
r
 
=
r
 
 (t + Dt) -
r
 
 (t) = æ
è 		x(t + Dt) - x(t), y(t + Dt) - y(t), z(t + Dt) - z(t) ö
ø
@
æ
è 		x¢(t) Dt, y¢(t) Dt, x¢(t) Dt ö
ø 		= Dt r¢(t).
Tällä välillä tehty työ on
DW @
F
 
 (
r
 
 (t)) ·D
r
 
 =
F
 
 (
r
 
 (t)) ·r¢(t) Dt.
Halutaan laskea työ, joka tehdään, kun massapiste siirtyy pisteestä A pisteeseen B. Jaetaan aikaväli [ a, b ] osaväleihin [ tk - 1, tk ], k = 1, ¼, n. Työksi osavälillä [ tk - 1, tk ] saadaan
DW @
F
 
 (
r
 
 (tk - 1)) ·r¢(tk - 1)(tk - tk - 1).
Koko työ on
DW @ n
å
k = 1 
F
 
 (
r
 
 (tk - 1)) ·r¢(tk - 1)(tk - tk - 1)
joka suppenee aikajaon tihentyessä kohti integraalia
b
ó
õ
a 
F
 
 (
r
 
 (t)) ·
r
 
 ¢(t) dt.
Tässä
b
ó
õ
a 
F
 
 (
r
 
 (t)) ·
r
 
 ¢(t) dt
=
b
ó
õ
a 
 æ
è 		F1(r(t))r1¢(t) + F2(r(t))r2¢(t) + F3(r(t))r3¢(t) ö
ø 		 dt
=

ó
õ
G 
 F1 dx + F2 dy + F3 dz,
eli tehty työ on edellämainitun käyräintegraalin arvo.

Käyräintegraalit voidaan määritellä helposti myös yleisemmille integroimisteille. Olkoot Gi ja Gk suunnistettuja säännöllisiä kaaria siten, että Gi:n loppupiste on Gi + 1:n alkupiste. Silloin Gi:t muodostavat paloittain säännöllisen tien G. (G = Èi = 1k Gi.) Määritellään

ó
õ
G 
 f1 dx1 + ¼+ fn dxn: = n
å
i = 1 
ó
õ
Gi 
 f1 dx1 + ¼+ fn dxn.

Esimerkki 17 Tutkitaan integraalia

ó
õ
G 
 y dx - x dy + dz.
a) G on jana jonka alkupiste on (1, 0, 0) ja loppupiste (0, 1, 1). G:n parametrisointi:
j(t) = (1 - t)(1, 0, 0) + t(0, 1, 1) = (1 - t, t , t) = : (j1, j2, j3),     t Î [ 0, 1 ].
Nyt
j1¢(t) = -1,     j2¢(t) = 1 = j3¢(t)
joten

ó
õ
G 
 y dx - x dy + dz
=
1
ó
õ
0 
 æ
è 		j2(t) j1¢(t) - j1(t) j2¢(t) + j3¢(t) ö
ø 		 dt
=
1
ó
õ
0 
 æ
è 		t ·(-1) - (1 - t) ·1 + 1 ö
ø 		 dt
=
t
ó
õ
0 
 -t - 1 + t + 1 dt = 0.

b) G on ruuviviiva
G = ì
í
î 		(cost, sint,  2
p
 t)   ê
ê 		 t Î é
ë 		0,  p
2
 ù
û 		ü
ý
þ 		,
Nyt
j1(t)
=
cost,
j2(t)
=
sint,
j3(t)
=
 2
p
 t
j1¢(t)
=
-sint,
j2¢(t)
=
cost,
j3¢(t)
=
 2
p
joten

ó
õ
G 
 y dx - x dy + dz
=
p/2
ó
õ
0 
 æ
è 		j2(t) j1¢(t) + j1(t) j2¢(t) + j3¢(t) ö
ø 		 dt
=
p/2
ó
õ
0 
 æ
è 		-sin2 t - cos2 t +  2
p
 ö
ø 		 dt
=
p/2
ó
õ
0 
 (-1+  2
p
 ) dt = -  2
p
 + 1 ¹ 0.

7.1  Vektorikentän potentiaali

Joukko A Ì Rn on alue, jos se on avoin ja yhtenäinen. (Joukko on yhtenäinen, jos sitä ei voi esittää kahden epätyhjän avoimen, erillisen joukon yhdisteenä).

Määritelmä 1 Olkoon A Ì °  R2 alue ja f : A ® R2, f = (f1, f2) vektorikenttä. Jos on olemassa differioituva funktio u : A ® R (skalaariarvoinen!) siten, että Ñu = f (eli f1 = D1u, f2 = D2u) niin u on funktion f potentiaali. Sanotaan myös, että lauseke
f1 dx1 + f2 dx2
on eksakti ja u on sen integraalifunktio.

Huomautus 2 Kaikilla vektorikentillä ei ole olemassa potentiaalia.

Huomautus 3 Potentiaali on yksikäsitteinen lisättävää vakiota vaille: Jos u on funktion f potentiaali, niin v : A ® R on funktion f potentiaali jos ja vain jos on olemassa vakio c Î R siten, että v = u + c.

Esimerkki 4 Olkoon
f(x, y) = (3x2y + cos(x + y), x3 + cos(x + y)),     f : R2 ® R2.
Tällöin
u(x, y) = x3y + sin(x + y),
ja pätee Ñu = f.

Esimerkki 5 Olkoon
f(x, y) = (10x2, cosx + ey).
Tällä ei ole potentiaalifunktiota. Tähän tapaukseen palaamme myöhemmin.

Edellä oleva Määritelmä 7.1.1 toimii myös avaruudessa Rn: Olkoon f : A ® Rn, missä A Ì Rn on alue. Tällöin u : A ® R on funktion f potentiaali, jos Ñu = f.

Esimerkki 6 Olkoon
f(x, y, z) = æ
è 		 x
r3
 ,  y
r3
 ,  z
r3
 ö
ø 		,    f : R3 \{
0
 
 } ® R3,
missä
r
 
=
(x, y, z) = x
i
 
 + y
j
 
 + z
k
 
 ,
r
=
ê
ê 		 
r
 
   ê
ê 		=
Ö
 
x2 + y2 + z2
 
 .
Voidaan kirjoittaa f(x, y, z) = [([`(r)])/(r3)]. Tällä on potentiaali u(x, y, z) = -[ 1/(r)], sillä
D1 u =  
x
 (-(x2 + y2 + z2)-[ 1/2]) =  1
2
 (x2 + y2 + z2)-[ 3/2] ·2x =  x
r3
 = f1 jne.

Lause 7 Olkoon f : A ® Rn jatkuva vektorikenttä, A Ì °  Rn alue ja f = (f1, ¼, fn). Olkoon u : A ® R funktion f potentiaali. Jos [`(a)] = (a1, ¼, an) Î A, [`(b)] = (b1, ¼, bn) Î A ja G Ì A paloittain säännöllinen tie alkupisteenä [`(a)] ja loppupisteenä [`(b)], niin

ó
õ
G 
 f1 dx1 + ¼+ fn dxn = u(
b
 
 ) - u(
a
 
 ).
Katso kuva 22.

kaari0.png
Figure 22: Kaari G

Todistus.  Oletetaan aluksi, että G on säännöllinen kaari, toisin sanoen, on olemassa jatkuvasti derivoituva parametriesitys
j = (j1, ¼, jn),     j: [ a, b] ® Rn.
Ketjusäännöstä seuraa, että
(u °j)¢(t) = n
å
i = 1 
 (Di u)(j(t)) ji¢(t) = n
å
i = 1 
 fi (j(t)) ji¢(t),    t Î [ a, b] Ì R.
Käyräintegraalin määritelmästä seuraa

ó
õ
G 
 f1 dx1 + ¼+ fn dxn
=
b
ó
õ
a 
 [ f1(j(t))j1¢(t) + ¼+ fn(j(t))jn¢(t) ] dt
=
b
ó
õ
a 
 (u °j)¢(t) dt = [ u °j]t = ab
=
u(j(b)) - u(j(a)) = u(
b
 
 ) - u(
a
 
 ).
    [¯]

Jos G on säännöllinen tie, jaetaan tarkastelu säännöllisiin osakaariin.

Esimerkki 8 Laske

ó
õ
G 

yz dx + xz dy + xy dz
(*) 
 ,
kun G on ruuviviiva,
ì
ï
í
ï
î
x
=
cost
y
=
sint
z
=
t
,    t Î [ 0, 2p].
Alkupiste on (1, 0, 0) ja loppupiste (1, 0, 2p).

Ratkaisu. Määritellään u(x, y, z) = xyz. Tällöin
Ñu(x, y, z) = (yz, xz, xy).
Siten (*) on eksakti funktio ja Lauseen 7.1.7 nojalla

ó
õ
G 
 yz dx + xz dy + xy dz = u(1, 0, 2p) - u(1, 0, 0) = 1 ·0 ·2p- 1 ·0 ·0 = 0.

Lause 9 Olkoon A Ì °  R2 ympyrä (kiekko), f : A ® R2 jatkuvasti derivoituva ja f = (f1, f2). Tällöin funktiolla f on potentiaali jos ja vain jos
D1 f2 = D2 f1        (integroituvuus ehto).

Huomautus 10 Lause 7.1.9 ei päde kaikilla alueille A; se voidaan kyllä yleistää niin sanotuille yhdesti yhtenäisille alueille. Katso kuva 23.

yhtenainen1.png
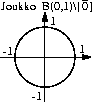yhtenainen2.png yhtenainen3.png
Yhdesti yhtenäinen Yhtenäisiä, mutta eivät yhdesti yhtenäisiä

Figure 23: Yhdesti yhtenäisyys

Lauseen 7.1.9 todistus. Väite: Funktiolla f on potentiaali jos ja vain jos D2 f1 = D1 f2.

Todistus.  1. Oletetaan, että funktiolla f on potentiaali u, eli
ì
í
î
D1 u
=
f1
D2 u
=
f2
.
Derivointijärjestys on vaihdannainen, joten
D1 (D2 u)
=
D2 (D1 u)
Þ D1 f2
=
D2 f1.
2. Oletetaan, että D2 f1 = D1 f2. Merkitään pisteellä (a, b) alueen A keskipistettä. Olkoon nyt (x, y) Î A mielivaltainen piste. Määritellään
u(x, y) : = y
ó
õ
b 
 f2 (a1, x2)  dx2 + x
ó
õ
a 
 f1(x1, y)  dx1 æ
è 		=
ó
õ
G 
 f1  dx1 + f2  dx2 ö
ø 		.
Lasketaan
D1 u(x, y) =

D1 y
ó
õ
b 
 f2(a, x2)  dx2
= 0
 
 
 + D1 x
ó
õ
a 
 f1(x1, y)  dx1 = f1(x, y),
ja
D2 u(x, y)
=
D2 y
ó
õ
b 
 f2(a, x2)  dx2 + D2 x
ó
õ
a 
 f1(x1, y)  dx1
=
f2(a, y) + x
ó
õ
a 
 D2 f1(x1, y)  dx1
=
f2(a, y) + x
ó
õ
a 
 D1 f2(x1, y)  dx1
=
f2(a, y) + [ f2(x1, y) ]x1 = ax
=
f2(a, y) + f2(x, y) - f2(a, y)
=
f2(x, y).
Perustelu sille, että tässä voidaan derivoida integraalimerkin alla, sivuutetaan.     [¯]

Esimerkki 11 Laske

ó
õ
G 
  2x(1 - ey)
(1 + x2)2
  dx +  ey
1 + x2
  dy,
kun
G = ì
í
î 		(x, y)   ê
ê 		 x = cost, y = sint, t Î é
ë 		0,  p
2
 ù
û 		ü
ý
þ 		.

Ratkaisu. Tien alkupiste on (1, 0) ja loppupiste (0, 1). Merkitään
f1(x, y)
=
 2x(1 - ey)
(1 + x2)2
f2(x, y)
=
 ey
1 + x2
Tällöin
D2 f1(x, y)
=
D2 é
ë 		 2x
(1 + x2)2
 -  2xey
(1 + x2)2
 ù
û 		= -  2x
(1 + x2)2
 ey
D1 f2(x, y)
=
D1  ey
1 + x2
 = -  ey ·2x
(1 + x2)2
 ,
eli D2 f1 = D1 f2. (Yhtälö D2 f1 = D1 f2 pätee koko tasossa R2, esimerkiksi joukossa B(0, 106).) Siten vektorikentällä f : = (f1, f2) on potentiaali u ja Lauseen 7.1.7 mukaan
u(0, 1) - u(1, 0) =
ó
õ
G 
 f1 dx + f2 dy.
Tämä voidaan tulkita myös niin, että integraalin arvo ei riipu integroimistiestä. Valitsemme uuden integroimistien [(G)\tilde] siten, että kuljetaan pisteestä (0, 1) pisteeseen (1, 0) koordinaattiakselien suuntaisia janoja pitkin origon kautta. Lasketaan

ó
õ
[(G)\tilde] 
 f1 dx + f2 dy =
ó
õ
G1 
 f1 dx + f2 dy +
ó
õ
G2 
 f1 dx + f2 dy
Tässä G1 : j(t) = (1 - t, 0), t Î [ 0, 1 ] ja j1¢ = -1, j2¢ = 0, joten

ó
õ
G1 
 f2 dy = 0    ja   f1(x, 0) =  2x(1 - e0)
(1 + x2)2
 = 0.
Siten

ó
õ
G1 
 = 0.
G2:n parametriesitys: j(t) = (0, t), t Î [ 0, 1 ] ja j1¢ = 0, j2¢ = 1.

ó
õ
G2 
 ¼ = 1
ó
õ
0 
  et
1 + 0
 j2¢(t) dt = 1
ó
õ
0 
 et dt = e - 1.
Vastaus on siis -1.

Esimerkki 12 Lause 7.1.9 ei päde kaikille alueille A!

Olkoon
f(x, y) = æ
è 		 -y
x2 + y2
 ,  x
x2 + y2
 ö
ø 		,    f: A ® R2,  A = R2 \{0, 0}.
Edelleen
D2 f1
=
 -(x2 + y2) + 2y2
(x2 + y2)2
 =  y2 - x2
(x2 + y2)2
D1 f2
=
 x2 + y2 - 2x2
(x2 + y2)2
 =  y2 - x2
(x2 + y2)2
siten D2 f1 = D1 f2 joukossa A. Tarkastellaan integraalia
ó
õ
f1 dx + f2 dy,
kun
G = { (x, y)   ê
ê 		 x = cost, y = sint; t Î [ 0, 2p] }
(eli G on yksikköympyrän reuna).

Jos funktiolla f on potentiaali u koko tasossa R2, niin Lauseen 7.1.7 nojalla
ó
õ
f1 dx + f2 dy = u(
b
 
 ) - u(
a
 
 ) = 0,
koska G:n loppupiste [`(b)] ja G:n alkupiste [`(a)] ovat sama (1, 0).

Lasketaan käyräintegraali suoraan:
j(t) = (cost, sint),     j1¢ = -sint, j2¢ = cost.
Näin ollen

ó
õ
G 
 f1 dx + f2 dy
=
2p
ó
õ
0 
 é
ë 		 -sint
1
 (-sint) +  cost
1
 ·cost ù
û 		 dt
=
2p
ó
õ
0 
 [ sin2 t + cos2 t ] dt
=
2p
ó
õ
0 
 1 dt = 2p ¹ 0.
Lause 7.1.9 ei näin ollen voi päteä.

Huomautus 13 Jos G on suljettu (umpinainen) integroimistie (alku- ja loppupiste samat), niin

ó
õ
G 
 f1 dx + f2 dy
(f kuten edellä) on "2p kertaa G:n kierrosluku nollan suhteen".

Lause 14 Olkoon A ympyrä, f: A ® R jatkuva. Funktiolla f on potentiaali u : A ® R, jos ja vain jos

ó
õ
G 
 f1 dx + f2 dy = 0,     (pyörteettömyys)
kun G on mielivaltainen umpinainen paloittain säännöllinen tie.

Potentiaalin laskeminen

Olkoon f : A ® R2 vektorikenttä, jolla on potentiaali u : A ® R. Lauseesta 7.1.7 seuraa
u(x, y) = -u(a, b) +
ó
õ
G 
 f1 dx1 + f2 dx2,
missä (a, b) Î A on kiinteä ja G Ì A on paloittain säännöllinen tie, alkupisteenä (a, b) ja loppupisteenä (x, y).

Jos esimerkiksi valitaan G:ksi murtoviiva (a, b) ® (a, y) ® (x, y) sekä u(a, b) = 0, saadaan u:n arvo pisteessä (x, y) kaavasta
u(x, y) = y
ó
õ
b 
 f2(a, x2) dx2 + x
ó
õ
a 
 f1(x1,y) dx1.
Vaihtoehtoisesti, jos G on murtoviiva (a, b) ® (x, b) ® (x, y), saadaan
u(x, y) = x
ó
õ
a 
 f1(x1, b) dx1 + y
ó
õ
b 
 f2(x, x2) dx2.
Katso kuva 24.

potentiaali1.png
Figure 24: Murtoviiva

Esimerkki 15 Laske vektorikentän
f : = (5x4y4, 4x5y3 + 1)
potentiaali.

Ratkaisu. 1) Tarkastellaan, onko potentiaalia: Pätee
D1 f2(x, y) = 20x4 y3 = D2 f1(x, y),     "(x, y) Î R2,
joten potentiaali u on olemassa koko tasossa.

2) Valitaan u(0, 0) = 0 ja G: (0, 0) ® (x, 0) ® (x, y). Saadaan
u(x, y)
=
x
ó
õ
0 
 f1(x1, 0) dx1 + y
ó
õ
0 
 f2(x, x2) dx2
=
x
ó
õ
0 
 5x14 ·0 dx1 + y
ó
õ
0 
 (4x5 x23 + 1) dx2
=
0 + [ x5 x24 + x2 ]x2 = 0y = x5 y4 + y.
Tarkistus:
Ñu(x, y) = (5x4 y4, 4x5 y3 + 1).

Potentiaalin laskeminen avaruudessa Rn

Olkoon A Ì Rn avoin yhtenäinen, f : A ® Rn vektorikenttä. Funktio u : A ® R on potentiaali, jos
Ñu = f     eli     Dj u = fj,      " j = 1, ¼, n.

Lauseen 7.1.9 integroituvuusehto avaruudessa Rn:
Di fj = Dj fi,      " i, j = 1, ¼, n,     i ¹ j.

Esimerkki 16 Olkoon
f(x, y, z) = æ
è 		y - sin(x + z), x, -sin(x + z) ö
ø 		.
Integroituvuus ehdot
D1 f2
=
1 = D2 f1
D1 f3
=
-cos(x + z) = D3 f1
D2 f3
=
0 = D3 f2
toteutuvat, joten
u(x, y, z) = xy + cos(x + z).

Tapauksessa n = 3 merkitään
Ñ×f
:=
  ê
ê
ê
ê
ê
ê
i
 
j
 
k
 
D1
D2
D3
f1
f2
f3
 ê
ê
ê
ê
ê
ê 		  =
i
 
   ê
ê
ê
D2
D3
f2
f3
ê
ê
ê 		 +
j
 
   ê
ê
ê
D1
D3
f1
f3
ê
ê
ê 		 +
k
 
   ê
ê
ê
D1
D2
f1
f2
ê
ê
ê 		 
=
(D2 f3 - D3 f2)
i
 
 + (D1 f3 - D3 f1)
j
 
 + (D1 f2 - D2 f1)
k
 
 .
Integroituvuusehto pätee jos ja vain jos Ñ×f = [`0] alueessa A.

Sanomme, että vektorikenttä f on pyörteetön, jos

ó
õ
G 
 f1 dx1 + ¼+ fn dxn = 0
jokaiselle umpinaiselle G.

7.2  Integrointi kaaren pituuden suhteen

Olkoon G Ì R2 säännöllinen kaari, j = (j1, j2) : [ a, b ] ® R kaaren G jatkuvasti derivoituva parametriesitys. Kaaren G pituus on
L = b
ó
õ
a 
Ö
 
j1¢(t)2 + j2¢(t)2
 
  dt.
Katso kuva 25.

kaari1.png
Figure 25: Kaaren pituus

Väliä [ a, t ] vastaava kaaren pituus
s = l(t) = t
ó
õ
a 
Ö
 
j1¢(t)2 + j2¢(t)2
 
  dt.

Funktio on l: [ a, b ] ® [ 0, L ] jatkuvasti derivoituva bijektio, koska
l¢(t) =
Ö
 
j1¢(t)2 + j2¢(t)2
 
 > 0.
l(t) on kaaren pituus pisteestä j(a) pisteeseen j(t) ja l on aidosti kasvava.

Määritellään y: = (y1, y2) : [ 0, L ] ® R2, y(s) = j°l-1(s). Funktion y on mittatarkka parametrisaatio polulle G, katso kuva 26.

kaari2.png
Figure 26: Parametrisaatio polulle G


ì
í
î
x
=
j1(t)
=
j1(l-1(s))
=
y1(s)
y
=
j2(t)
=
j2(l-1(s))
=
y2(s)
 ,     0 £ s £ L.

Olkoon f : G® R jatkuva. Määritellään funktion f integraali kaaren pituuden suhteen

ó
õ
G 
 f ds : = L
ó
õ
0 
 f(y(s)) ds.
Laskujen helpottamiseksi suoritetaan muuttujan vaihto:
s
=
l(t) = t
ó
õ
a 
Ö
 
j1¢(t)2 + j2¢(t)2
 
  dt,
 ds
dt
=
 d
dt
 t
ó
õ
0 
Ö
 
j1¢(t)2 + j2¢(t)2
 
 : =
Ö
 
j1¢(t)2 + j2¢(t)2
 
 .
Saadaan

ó
õ
G 
 f ds = L
ó
õ
0 
 f(y(s)) ds = b
ó
õ
a 
 f(j(t))
Ö
 
j1¢(t)2 + j2¢(t)2
 
  dt.
Integraalin geometrinen tulkinta: se on funktion f kuvaajan ja x-y-tasossa olevan käyrän G väliin jäävän liuskan pinta-ala. Katso kuva 27.

kaari3.png
Figure 27:

Avaruudessa R3:

ó
õ
G 
 f ds = b
ó
õ
a 
 f(y(s)) ds = b
ó
õ
a 
 f(j(t))
Ö
 
j1¢(t)2 + ¼+ jn¢(t)2
 
  dt,
missä j: [ a, b ] ® Rn, on G:n parametriesitys.

Esimerkki 1 (Katso kuva 28.) Jos kaarella G on massa, jonka tiheys r(x, y), niin painopisteen koordinaatit ovat:
X
=

ó
õ
G 
 xr(x, y),ds

ó
õ
G 
 r(x, y) ds
 ,
Y
=

ó
õ
G 
 yr(x, y),ds

ó
õ
G 
 r(x, y) ds
 .

kaari4.png
Figure 28:

Esimerkki 2 Oletetaan, että r on vakio=:r ja G on puoliympyrä
{ (x, y)   ê
ê 		 x2 + y2 = 1, y ³ 0 }.
Reunalla G on parametriesitys
ì
í
î
x
=
cost = : j1(t)
y
=
sint = : j2(t)
 ,     t Î [ 0, p].
Lasketaan

ó
õ
G 
 r(x, y) ds = p
ó
õ
0 
 r0
Ö
 
sin2(t) + cos2(t)
 
  dt = r0p
ja

ó
õ
G 
 xr(x, y) ds
=
p
ó
õ
0 
 r0 j1(t)
Ö
 
j1¢(t)2 + j2¢(t)2
 
  dt = p
ó
õ
0 
 r0 cost dt = 0

ó
õ
G 
 yr(x, y) ds
=
p
ó
õ
0 
 r0 sint dt = 2r0
eli
X =  0
pr0
 = 0,     Y =  2r0
pr0
 =  2
p
 .

8  Pintaintegraalit

Olkoon R Ì R2 suljettu suorakulmio
[ a, b ] ×[ c, d ] = { (x, y)   ê
ê 		 a £ x £ b, c £ y £ d },
ja a, b, c, d Î Z. Olkoon n Î N ja Dn joukko tason suljettuja neliöitä:
Dn = ì
í
î 		[ k ·2-n, (k + 1)2-n ]×[ l2-n, (l + 1)2-n ]   ê
ê 		 k, l Î Z ü
ý
þ 		.
Merkitään
Qn,k,l = [ k2-n, (k + 1)2-n ] ×[ l2-n, (l + 1)2-n ]
Èk, l Î Z Qn, k, l = R2. Katso kuvat 29 ja 30.

pinta1.png
Figure 29: Hila

pinta2.png
Figure 30: Pinta

Olkoon f : R® R jokin funktio. Haluamme määritellä sen integraalin yli joukon R. Merkitään
Gn, k, l = sup
{ f(x, y)   ê
ê 		 (x, y) Î Qn, k, l }
ja
gn, k, l = inf
{ f(x, y)   ê
ê 		 (x, y) Î Qn, k, l }
(määrittely: jos Qn, k, l \not Ì R Þ Gn, k, l gn, k, l = 0). Määritellään lukua n vastaavat ylä- ja alasummat:
Mn
=

å
k, l 
 Gn, k, l ·2-2n
mn
=

å
k, l 
 gn, k, l ·2-2n
Huom! 2-2n on Qn, k, l:n pohjan pinta-ala, joten esimerkiksi luku Gn, k, l ·2-2n on kuvassa 30 olevan särmiön tilavuus. Luku gn, k, l ·2-2n on hieman pienemmän särmiön tilavuus; luku Mn on siten (hieman liian suuri) approksimaatio funktion f määräämän pinnan ja x-y-tason suorakulmion R väliin jäävän kappaleen tilavuudelle.

Määritelmä 3 Jos limn ® ¥ Mn ja limn ® ¥ mn ovat olemassa ja

lim
n ® ¥ 
 Mn =
lim
n ® ¥ 
 mn,
niin sanotaan, että f on integroituva joukossa R ja kyseinen raja-arvo on funktion f pintaintegraali yli suorakulmion R, merkitään

ó
õ
R 
 f,    
ó
õ
R 
 ó
õ 		f(x, y) dxdy,     b
ó
õ
a 
 d
ó
õ
c 
 f(x, y) dxdy.

Huomautus 4 Voidaan osoittaa, että jos f : R ® R on jatkuva, se on aina integroituva.

Olkoon A Ì R2 rajoitettu, f : A ® R. Määritellään funktio f koko joukossa R kaavalla
f(x, y) : = 0,     kun (x, y) Ï A.
Merkitään fA:lla funktion f jatketta. Valitaan suorakulmio R (reunat kokonaislukujen kohdalla kuten edellä) siten, että A Ì R. Määritellään

ó
õ
A 
 f : =
ó
õ
R 
 fA,
määritelmä ei riipu suorakulmion R valinnasta. Katso kuva 31.

pinta3.png
Figure 31:

Jos A ei ole rajoitettu, voidaan määritellä

ó
õ
A 
 f =
lim
m ® ¥ 
ó
õ
A ÇB(0, m) 
 f,
mikäli kyseinen raja-arvo on olemassa. Katso kuva 32.

pinta4.png
Figure 32:

Olkoon A Ì R2 rajoitettu. Määritellään joukon A karakteristinen funktio kaavalla
XA(x, y) = ì
í
î
1,
(x, y) Î A
0,
(x, y) Ï A.

Määritelmä 5 A on mitallinen, jos XA on integroituva A:ssa. Katso kuva 33.

pinta5.png
Figure 33:

Huomautus 6 Itse asiassa

ó
õ
A 
 XA = A:n ¢¢pinta-ala¢¢.

òA XA = A:n pintamitta =: m(A). Jos m(A) = 0, niin sanotaan, että A on nollamittainen.

Lause 7 Jos joukon A reuna on nollamitallinen, niin A on mitallinen.

Lause 8 Jos kaari on säännöllinen tai muotoa
{ (x, y)   ê
ê 		 x Î [ a, b ], y = y(x) },
missä y: [ a, b ] ® R on jatkuva, niin se on nollamittainen.

Huomautus 9 Nollamittaisten joukkojen äärellinen yhdiste on nollamittainen. Kochin lumihiutalekäyrä (katso kuva 34) on esimerkki monimutkaisesta tason osajoukosta, ns. fraktaalista. Fraktaalireunaiset joukot eivät yleensä ole mitallisia edellä esitetyssä mielessä, eikä niiden yli voida integroida tällä tekniikalla.

koch.png
Figure 34: Kochin lumihiutalekäyrä

Lause 10 Jos funktiot f1, ¼, fm ovat integroituvia A:ssa ja l1, ¼, lm Î R, niin funktio
l1f1 + ¼+ lmfm
on integroituva A:ssa, ja

ó
õ
A 
 l1f1 + ¼+ lmfm = l1
ó
õ
A 
 f1 + ¼+ lm
ó
õ
A 
 fm.

Lause 11 Olkoon A Ì R2, m(d(A)) = 0. Olkoon f : A ® R sellainen funktio, että f on jatkuva lukuunottamatta mahdollisesti jotain A:n nollamittaista osajoukkoa B. Silloin f on integroituva A:ssa.

Esimerkki 12 Olkoon A = B((3,4), 100) ja
f(x, y) = ì
í
î
sin(x + y),
kun y ³ 0
-1,
kun y < 0.
Tämä ei ole jatkuva x-akselilla (=L), mutta L ÇA on nollamittainen(jana).

Lause 13 Olkoon A joukko, joka on jaettu osiin Ai, i = 1, ¼, n, missä m(d(Ai)) = 0. Funktio f on integroituva joukossa A jos ja vain jos f on integroituva jokaisessa joukossa Ai. Tällöin

ó
õ
A 
 f =
ó
õ
A1 
 f + ¼+
ó
õ
An 
 f = n
å
i = 1 
ó
õ
Ai 
 f.

Lause 14 Oletetaan että f on integroituva joukossa
R = { (x, y)   ê
ê 		 a £ x £ b, c £ y £ d },
ja jokaisella kiinteällä x Î [ a, b ], funktio y ® f(x, y) on integroituva (y:n suhteen) välillä [ c, d ]. Silloin funktio
g(x) = d
ó
õ
c 
 f(x, y) dy
on integroituva välillä [ a, b ], ja pätee

ó
õ
R 
 f = b
ó
õ
a 
 g(x) dx = b
ó
õ
a 
 æ
è 		d
ó
õ
c 
 f(x, y) dy ö
ø 		dx.
Merkitään
b
ó
õ
a 
 d
ó
õ
c 
 f(x, y) dx dy     æ
è 		tai joskus myös     b
ó
õ
a 
 d
ó
õ
c 
 f(x, y) dy dx ö
ø 		.

Esimerkki 15 Laske

ó
õ
R 
 (1 - 6x2y),
kun R = [ 0, 2 ]×[ -1, 1 ] = { (x, y)  | 0 £ x £ 2, -1 £ y £ 1 }.

Ratkaisu.

ó
õ
R 
=
2
ó
õ
0 
 1
ó
õ
-1 
 (1 - 6x2 y) dx dy = 2
ó
õ
0 
 æ
è 		1
ó
õ
-1 
 (1 - 6x2y) dy ö
ø 		dx
=
2
ó
õ
0 
 æ
è 		é
ë 		y - 3x2y2 ù
û 		1
y = -1 
 ö
ø 		dx = 2
ó
õ
0 
 (1 - 3x2 ·1) - (-1 -3x2(-1)2) dx
=
2
ó
õ
0 
 2 dx = 4.

Lause 16 Olkoot f1 : [ a, b ] ® R, f2 : [ a, b ] ® R jatkuvia funktioita, joille f1(x) < f2(x),  " x Î ] a, b [ sekä f1(a) £ f2(a), f1(b) £ f2(b). Oletetaan, että f : A ® R on integroituva, missä
A = { (x, y)   ê
ê 		 x Î [ a, b ], f1(x) £ y £ f2(x) }.
Oletetaan, että integraali
f2(x)
ó
õ
f1(x) 
 f(x, y) dy
on olemassa kaikille x Î [ a, b ]. Silloin

ó
õ
A 
 f = b
ó
õ
a 
 æ
è 		f2(x)
ó
õ
f1(x) 
 f(x, y) dy ö
ø 		dx.
Katso kuvat 35 ja 36.

integraali1.png
Figure 35:

integraali2.png
Figure 36:

Esimerkki 17 Olkoon f1(x) = 0, f2(x) = x ja f(x, y) = 3 - x - y. Nyt x Î [ 0, 1 ], joten

ó
õ
A 
=
1
ó
õ
0 
 æ
è 		x
ó
õ
0 
 3 - x - y dy ö
ø 		dx = 1
ó
õ
0 
 é
ë 		3y - xy -  1
2
 y2 ù
û 		x

y = 0 
  dx
=
1
ó
õ
0 
 (3x - x2 -  1
2
 x2) dx = 1
ó
õ
0 
 (3x -  3
2
 x2) dx
=
ó
õ
 é
ë 		 3
2
 x2 -  1
2
 x3 ù
û 		1

x = 0 
 = 1.
Katso kuva 37.

integraali3.png
Figure 37: 2.ratkaisu

Erityisesti siinä tapauksessa, että f on jatkuva, edellä mainitut integraalit ovat olemassa ja kaava pätee.

Vastaavasti: Jos integroimisalue A on muotoa
A = {(x, y)   ê
ê 		 c £ y £ d, y1(y) £ x £ y2(y) }
ja f on jatkuva A:ssa, niin

ó
õ
A 
 f = d
ó
õ
c 
 æ
è 		y2(y)
ó
õ
y1(y) 
 f(x, y) dx ö
ø 		dy.
(Tässä y1(y) < y2(y) kaikilla y Î [ c, d ] jne.)

Edellinen esimerkki voidaan siis laskea myös seuraavasti:

f(x, y) = 3 - x - y, y Î [ 0, 1 ] ja y1(y) £ x £ y2(y). Nyt y £ x £ 1 eli y1(y) = y ja y2(y) = 1. Saadaan

ó
õ
A 
 f(x, y)
=
1
ó
õ
0 
 æ
è 		1
ó
õ
y 
 f(x, y) dx ö
ø 		dy = 1
ó
õ
0 
 é
ë 		3x -  1
2
 x2 - xy ù
û 		1

x = y 
  dy
=
1
ó
õ
0 
 æ
è 		3 -  1
2
 - y - æ
è 		3y -  1
2
 y2 - y2 ö
ø 		ö
ø 		 dy
=
1
ó
õ
0 
 æ
è 		 3
2
 y2 - 4y +  5
2
 ö
ø 		dy = ¼ = 1.

Esimerkki 18 Integroimisjärjestyksen vaihtaminen (katso kuva 38). Tarkastellaan integraalia
I = 2
ó
õ
0 
 æ
è 		2x
ó
õ
x2 
 (4x + 2) dy ö
ø 		dx,
(25)
Tässä x Î [ 0, 2 ], x2 : = f1(x) £ y £ f2(x) : = 2x; huomaa, että kun x £ 2, niin x2 = x ·x £ 2x. Tehtävänä on lausua integraali 25 muodossa
d
ó
õ
c 
 æ
è 		y2(y)
ó
õ
y1(y) 
 (4x + 2) dx ö
ø 		dy,
missä y Î [ 0, 4 ], siis c = 0,  d = 4. Mutta mitä ovat funktiot y1, y2?

integraali4.png
Figure 38: Integrointijärjestys

Reunakäyrällä f1 pätee eli y = f1(x) = x2 jos Öy = x; siten y2(y) = Öy (katso kuva 38). Reunakäyrällä f2 on y = f2(x) = 2x eli x = [(y)/2]; siten y1(y) = [(y)/2]. Siis,
I = 4
ó
õ
0 
 æ
è 		Öy
ó
õ
y/2 
 (4x + 2) dx ö
ø 		dy.

8.1  Muuttujien vaihto pintaintegraaleissa

Lause 1 Olkoon A Ì R2 rajoitettu, ja d(A) nollamittainen ja f : A ® R jatkuva. Oletetaan, että on olemassa jatkuvasti derivoituva bijektio g : R ® A, missä R Ì R2 on suorakulmio. Tällöin

ó
õ
A 
 f =
ó
õ
R 
 (f °g) ·| Jg |,
missä Jg on funktion g funktionaalideterminantti eli jakobiaani,
Jg =   ê
ê
ê
D1g1
D2g1
D2g2
D2g2
ê
ê
ê 		  = (D1g1)(D2g2) - (D2g1)(D1g2),
missä g = (g1, g2). Katso kuva 39.

pintaint1.png
Figure 39: Pintaintegraali

Esimerkki 2 Olkoon
A : = { (x, y)   ê
ê 		 x2 + y2 £ a2 }.
Huomaa, että yllä x Î [ -a, a ] ja
f1(x) = -
Ö
 
a2 - x2
 
 £ y £
Ö
 
a2 - x2
 
 = f2(x).
Tämä saattaa johtaa vaikeaan x-integraaliin. Tarkastellaan sen vuoksi funktiota g : R ® A,
g(r, j) = (r cosj, r sinj),
missä r Î [ 0, a ] ja j Î [ 0, 2p] eli (r, j) Î R: = [ 0, a ] ×[ 0, 2p]. Tämä g on surjektio.

Huomautus 3 Jos 1. g : R ® A on injektio ja m(A \g(R)) = 0 tai 2. g : R ® A on surjektio, ja ne pisteet, joilla on enemmän kuin yksi alkukuva muodostavat nollajoukon, niin Lause pätee edelleen.

Nyt
Jg = D1g1D2g2 - D2g1D1g2 = cosjr cosj- r(-sinj)sinj = r(cos2j+ sin2j) = r.
Siis,

ó
õ
A 
 f = a
ó
õ
0 
 p
ó
õ
0 
 f(rcosj, rsinj)r dr dj.

Huomautus 4 Lause 8.1.1 pätee yleisimmillekin joukoille R kuin suorakulmioille.

8.2  Käyrä- ja pintaintegraalien yhteys

Lause 1 (Eräs Greenin kaavoista) Olkoon A Ì R2 on rajoitettu ja d(A) Jordanin-käyrä joka koostuu äärellisestä määrästä säännöllisiä kaaria. Olkoon f : A ® R2 on jatkuvasti derivoituva. Silloin

ó
õ
A 
 (D1f2 - D2f1) =
ó
õ
dA 
 f1 dx + f2 dy.
Oletetaan myös, että d(A):lla on jatkuvasti derivoituva parametriesitys j: D® dA siten, että j¢(t) ¹ 0 kaikilla t Î D. Tällöin

ó
õ
A 
 (D1f1 + D2f2) =
ó
õ
dA 
 (f ·
n
 
 ) ds,
(26)
missä [`(n)] on reunakäyrän ulkonormaali: | [`(n)] | = 1, | [`(n)] | ^d(A):n tangentti.

8.3  Integrointi yli pinnan

Olemme käsitelleet edellä, kuinka integroidaan yli tasoalueiden. Tällaista integraalia sanotaan pintaintegraaliksi, ja se palautuu kaksinkertaiseen yhden muuttujan funktion integrointiin.

Seuraavaksi otetaan hiukan yleisempi tapaus: integroidaan yli pinnan, joka ei enää olekaan xy-tason alue, vaan pinta
E: = { ( x, y, z) Î R3   ê
ê 		 z = h(x, y), (x, y) Î A },
missä A on joku sopiva xy-tason osajoukko. Joukko E on siis R3:n osajoukko, pinta, joka on kahden muuttujan funktion h kuvaaja (esimerkiksi A:n yläpuolella). (Piirrä kuva, kun esimerkiksi A on tason yksikköneliö, ja h on funktio h(x,y) = 1 + x2).

Oletamme, että kolmen muuttujan funktio f on määritelty joukossa E. Silloin sen integraalia yli pinnan E merkitään

ó
õ
E 
 f
(27)
ja se määritellään kaavalla

ó
õ
E 
 f : =
ó
õ
A 
 f(x, y, h(x,y))
Ö
 
1 + D1 h(x,y)2 + D2 h(x,y)2
 
  dx dy.
(28)

Huomautus 1 Siinä tapauksessa, että f on vakiofunktio 1, tämä integraali antaa pinnan E pinta-alan.

Esimerkki 2 Tarkastellaan funktion h(x,y): = Ö{1 - x2 - y2} määräämää pintaa E joukossa R3, kun (x,y) Î A, ja A on xy-tason yksikkökiekko (siis joukko {x2 + y2 < 1}). Piirrä kuva: Pinta E on avaruuden yksikköpallon kuoren ylempi puolikas.

Laskemme E:n pinta-alan, eli integroimme vakiofunktiota (25) yli pinnan E.

Saamme ensinnäkin (laske!)
D1 h (x,y)2 =   x2
1 - x2 - y2
(29)
ja
D2 h (x,y)2 =   y2
1 - x2 - y2
.
(30)
Edelleen kaavassa (28)

Ö
 
1 +D1 h(x,y,)2 + D2 h(x,y)2
 
=
  æ
Ö
1 +   x2
1 - x2 - y2
+   y2
1 - x2 - y2
 
=
  æ
Ö
  1
1 - x2 - y2
 
Siirtymällä napakoordinaatteihin saadaan (28) muotoon

ó
õ
A 
   1

Ö
1 - x2 - y2
 dx dy
=

ó
õ
A 
   1

Ö
1 - ( x2 + y2)
 dx dy
=
1
ó
õ
0 
 2 p
ó
õ
0 
   1

Ö
1 - r2
 r dr dq
=
2p 1
ó
õ
0 
   1

Ö
1 - r2
r dr = 2 p.

Stokesin kaavan käsittely joudutaan jättämään ajan puutteen vuoksi pois. Katso tarvittaessa kirjallisuudesta.

9  Avaruusintegraalit

Siirrymme tarkastelemaan kolmen muuttujan funktioiden integrointia yli avaruuden R3 osajoukon A. Ajatus on siis se, että yleistetään aiempi tasoalueiden yli integrointi (ei yllä oleva ïntegrointi yli pinnan", vaan sitä edeltävä tarkastelu) tapaukseen jossa on yksi muuttuja enemmän.

Integraalin käsite ja siihen liittyvät mittateoreettiset käsitteet määritellään analogisesti kahden muuttujan funktion tapauksen kanssa. Jätämme tässä yksityiskohdat väliin.

Avaruusintegraalia merkitään esim.

ó
õ
A 
 f     tai     ó
õ
ó
õ
A 
 ó
õ 		f(x,y,z) dx dy dz.

Kuten arvata saattaa pintaintegraalien tapauksesta, avaruusintegraalin laskeminen palautuu kolminkertaiseen integrointiin. Olkoon ensiksi A koordinaattiakselien suuntainen suuntaissärmiö
A : = { (x,y,z)  |  a1 £ x £ a2 , b1 £ y £ b2 , c1 £ z £ c2 }
eli A = [a1, a2] ×[b1, b2] ×[c1, c2], missä a1 jne. ovat jotain reaalilukuja. Tällöin

ó
õ
A 
 f = a2
ó
õ
a1 
 æ
è 		b2
ó
õ
b1 
 æ
è 		c2
ó
õ
c1 
 f (x,y,z) dz ö
ø 		dy ö
ø 		dx.
(31)

Olettaen että f on riittävän siisti, esimerkiksi jatkuva, joukossa A, integroinnit kaavassa (31) voi suorittaa missä järjestyksessä tahansa:

ó
õ
A 
 f = b2
ó
õ
b1 
 æ
è 		c2
ó
õ
c1 
 æ
è 		a2
ó
õ
a1 
 f (x,y,z) dx ö
ø 		dz ö
ø 		dy = c2
ó
õ
c1 
 æ
è 		b2
ó
õ
b1 
 æ
è 		a2
ó
õ
a1 
 f (x,y,z) dx ö
ø 		dy ö
ø 		dz ¼

Integraalit yli monimutkaisempien joukkojen lasketaan kuten kahden muuttujan tapuksessakin. Oletetaan, että on annettu kahden muuttujan funktiot j1 ja j2, missä j1(x,y) £ j2 (x,y), kun a1 £ x £ a2 ja b1 £ y £ b2. Olkoon nyt
A : = { (x,y,z)  |  a1 £ x £ a2 , b1 £ y £ b2 ,j1 (x,y) £ z £ j2 (x,y) } .
(Hahmottele kuva joukosta A, kun j1 ja j2 ovat jotain sopivia funktioita.) Tällöin

ó
õ
A 
 f = a2
ó
õ
a1 
 æ
è 		b2
ó
õ
b1 
 æ
è 		j2 (x,y)
ó
õ
j1 (x,y) 
 f (x,y,z) dz ö
ø 		dy ö
ø 		dx.
Tässä x- ja y-integrointien järjestyksen voi vaihtaa.

Vielä yleisemmin, jos
A : = { (x,y,z)  |  a1 £ x £ a2 , y1(x) £ y £ y2 (x) , j1 (x,y) £ z £ j2 (x,y) }
joillekin sopiville funktioille y1 jne., niin

ó
õ
A 
 f = a2
ó
õ
a1 
 æ
è 		y2 (x)
ó
õ
y1(x)  
 æ
è 		j2 (x,y)
ó
õ
j1 (x,y)  
 f (x,y,z) dz ö
ø 		dy ö
ø 		dx.

9.1  Muuttujan vaihto avaruusintegraalissa

Olkoon R Ì R3 koordinaattiakselien suuntainen suuntaissärmiö, A Ì R3 kuten yllä sekä g : R® A jatkuvasti derivoituva bijektio. Olkoon f joukossa A määritelty funktio, jota halutaan integroida. Pintaintegraalien tapaan voidaan suorittaa muuttujanvaihto kaavalla

ó
õ
A 
 f =
ó
õ
R 
 (f °g) | Jg |,
missä Jg on kuvauksen g Jacobin determinantti ( 3 ×3-determinantti, jonka j:nnen rivin i:s alkio on Di gj).

Tarkastellaan tapausta, että g välittää siirtymisen pallokoordinaatteihin, eli g : R ® A ,
g( r, j, y) : = ( r cosjcosy, r cosjsiny, r sinj)

R: = { (r , j, y)  |  0 £ r £ a , -p/ 2 £ j £ p/2, 0 £ y £ 2 p}
ja A on avaruuden 0-keskinen, a-säteinen pallo
A = { (x,y,z)  |  x2 + y2 + z2 £ a2 },
Tällöin Jg on
Jg (r,j, y) = r2 cosj.

9.2  Pinta-ja avaruusintegraalien välinen yhteys

Olkoon A Ì R3 suljettu ja rajoitettu joukko, jonka reuna muodostaa pinnan S. Olkoon f: A ® R3 määritelty jatkuvasti derivoituva vektorikenttä sekä [`(n)] pinnan S ulkonormaali(vektori). Divergenssikaava yhdistää avaruus- ja pintaintegraalit seuraavasti:

ó
õ
A 
 Ñ·f =
ó
õ
S 
 f ·
-
n
 
 .
Mikäli vektorikentällä f on potentiaali u, eli f = Ñu, saadaan erikoistapauksena Gaussin kaava

ó
õ
A 
 Du =
ó
õ
S 
 [`(n)] u.



File translated from TEX by TTH, version 3.01.
On 27 Sep 2002, 11:30.