Differentiaaliyhtälöt, syksy 2001
Harjoitus 1a (kotilaskut, tarkastus ke 12.9. luennolla 16-18 M2)
  1. a) Piirrä yhtälön xy¢ = 2y suuntakenttää suorakulmiossa [-2,2]×[-4,4].

    2. b) Näytä, että funktiot y, y(x) : = cx2, ovat yhtälön xy¢ = 2y ratkaisuja.
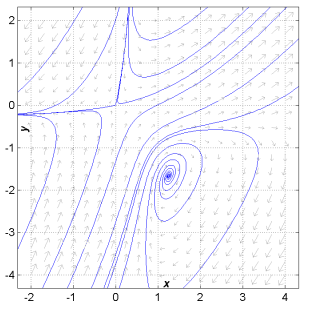
    c) Piirrä suuntakenttääsi ratkaisuja vakion arvoilla c = 0, ± 1/2, ±1, ±2.
  2. Selvitä, missä tason osa-alueissa lausekkeen
    3. f(x,y): =   ln(-x)
    1 - x2 - y2
    määrittelemä funktio on (äärellisenä) määritelty.
    Millä arvoilla x Î R kuvaus y® f(x,y) on derivoituva?
    Missä alueissa differentiaaliyhtälö y¢ = f(x,y) on määritelty?
    Ratkaise tehtävien 3-5 differentiaaliyhtälöt (integroimalla)
  3. y¢ =  3/(2-x) ja y¢ =  3 / (2-x)2
  4. y¢ = 3e4x+5 ja y¢ = (x-1)e2x
  5. y¢ = (ln3x) / (2x)
  6. Mitkä funktioista y1(t) : = 1+t, y2(t) : = 1+2t ja y3(t) : = 1 ovat differentiaaliyhtälön
    7.  dy
    dt    		 =   y2-1
    t2 + 2t
    ratkaisuja?
  7. Mikä vasemmista faasitason käyristä lienee kuvattuna muuttujan t funktiona oikeanpuoleisessa kuvassa?

    8.