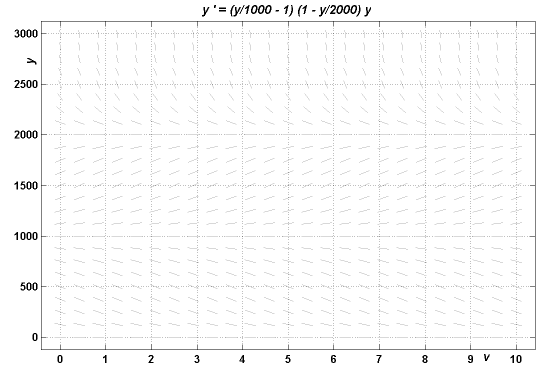
Figure 1: Eliöpopulaation määrä
| a) | y¢ / y = x2+x | b) | y¢ /(1 + y2) = cosx | c) | yy¢e-y2 = 1 |
Vihje: Yhtälöiden vasemmat puolet ovat eräiden funktioiden derivaattoja.
|
| 1) | xy¢¢+ 2y sin x = eyx, y(1) = y¢(1) = 2 | 2) | y¢+ y cos(x) = y sin x |
| 3) | y¢y¢¢ = 1 + y2, y(0) = 2, y(1) = 1 | 4) | ¶u/¶x + u = Ö{¶2 u / ¶y2} |
| 5) | ¶x/¶t = 2x-3xy, ¶y / ¶t = 4xy-5y, x(1) = 1, y(1) = 0 |
seuraavat asiat (tehtävät 3-4):
3. a) Onko yhtälö tavallinen vai osittaisdifferentiaaliyhtälö?
b) Mikä on yhtälön kertaluku?
c) Onko alkuarvo- tai reuna-arvotehtävä?
4. d) Onko yhtälö normaalimuotoinen?
e) Onko yhtälö lineaarinen?
f) Onko yhtälö autonominen?
6. Muunna 1. kertaluvun differentiaaliyhtälöryhmäksi y¢¢¢ = 2y2y¢+ 3xy¢¢.
7. Muodosta differentiaaliyhtälöryhmä (ja sille alkuarvot), jolla on ratkaisuna käyrä
| x1(t) | = | a(t + sint) |
| x2(t) | = | a(1 + cost) |
8. Differentiaaliyhtälön y¢=f(x,y) vakioratkaisua y=A sanotaan tasapainoratkaisuksi (equilibrium ) ja arvoa A tasapainotilaksi . Kuvassa erään eliöpopulaation lukumäärää ajan (vuosina) funktiona kuvaavan differentiaaliyhtälön suuntakenttää. Piirrä kenttään useita eri tyyppisiä ratkaisukäyriä ja kuvaile kehitystä eri alkuarvoilla hetkellä 0. Määritä tasapainotilat.

9. a) Piirrä Kuvassa vasemmalla olevaan faasipiirrokseen sen viereisessä kuvattua ratkaisuparia vastaava käyrä ja
b) selvitä, milloin saalistajakanta on suurimmillaan ja paljonko silloin on uhreja.
c) Kuvaile tilanteen kehittymistä tilasta, jossa uhreja on 300 ja saalistajia 200.
d) Onko havaittavissa tasapainotiloja (miten se tässä määriteltäisiinkään)?
|