Differentiaaliyhtälöt, syksy 2001
Harjoitus 3

Matematiikan laitos järjestää kotitehtävien ohjausta viikoilla 37-49 (10.9.-5.12.) salissa M9 aikoina ma 14-18, ti 14-18 ja ke 14-16.

1. Ratkaise alkuarvotehtävä
y¢¢+   1
x		 - x = 0,    y(1) = -  1
2		 , y¢(1) = 2.
Missä ratkaisu on määritelty?

2. Piirrä tasavälinen suuntakenttä yhtälölle y¢ = -2ty2 neliöön [0,2]×[0,2] käyttäen väliä 0.5.

3. a) Ratkaise graafisesti (esimerkiksi edellisen suuntakentän avulla)
y¢ = -2ty2,     y(0) = 1,
(1)
ja määritä sen avulla likiarvot luvuille
y(0.5)       y(1)       y(1.5)       y(2).
(2)
b) Ratkaise (eksaktisti) alkuarvotehtävä 1 ja laske yo. lukujen 2 tarkat arvot.

4. Laske numeerisesti alkuarvotehtävän 1 avulla
a) Eulerin menetelmällä askelvälinä 0.5
b) Runge-Kutta-menetelmällä askelvälinä 1
taulukot, piirrä vastaavat approksimaatiot ja määritä arviot yo. luvuille 2.


5. Muodosta yhtälön y¢ = x - 2y isokliinikenttää neliössä [-3,3]×[-3,3] ja kuvaile kvalitatiivisesti ratkaisujen käytöstä.

6. Ratkaise graafisella murtoviivakonstruktiolla alkuarvotehtävät
a) y¢ = x - 2y,     y(0) = 1,
b) y¢ = x - 2y,     y(-3) = 3,

välillä [-3,3]. Miten pieni askelväli näyttäisi näissä johtavan kohtuullisen sievään arvioon (siis ei tule ihme hässäkkää, kuten esim. askelvälillä 1.0)? Yhtälön tasavälistä suuntakenttää kuvassa 1.


7. Ratkaise luennolla jaetussa (englanninkielisessä) kopiossa oleva tehtävä 1.1#4.
Siinä slope = kulmakerroin, undefined tarkoittaa yleisesti määrittelemätöntä, tässä arvoja ±¥. Voit käyttää halutessasi Polkingin DFIELDiä tai muuta vastaavaa, mutta parempi olisi pystyä selviytymään ilman.
Paperin kääntöpuolen Tehtävä 1.1#5 ratkaistaneen myöhemmin.
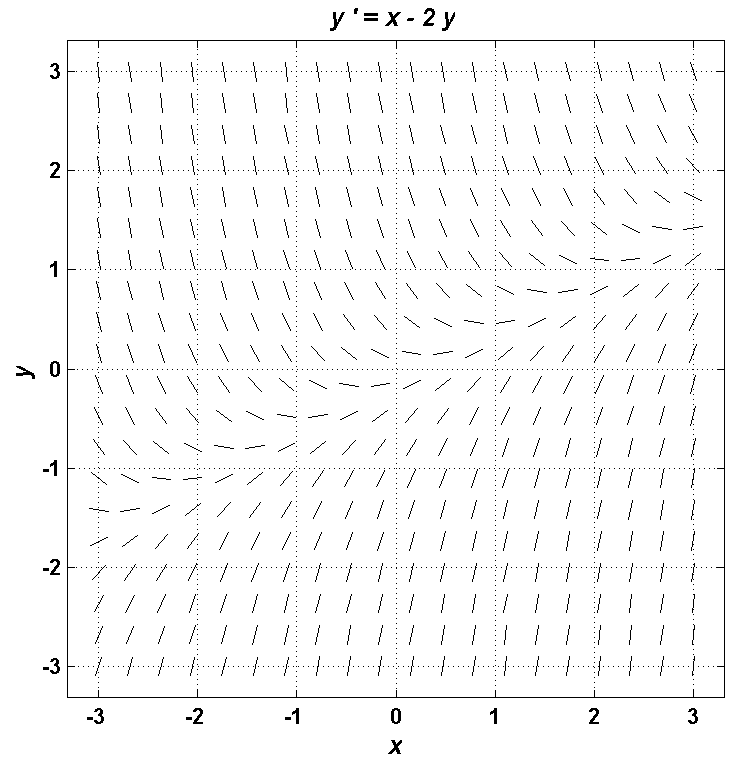
DYKuv01/K03016.png
Figure 1: Tehtävässä 6 luvattu suuntakenttä

File translated from TEX by TTH, version 3.01.
On 17 Sep 2001, 14:21.