Differentiaaliyhtälöt, syksy 2001
Harjoitus 5

Viikolla 1.-5.10. on vain torstaiaamun demot 8-10 M6. Lisäksi on yksi demoryhmä seuraavan viikon maanantaina 8.10. klo 14-16 salissa M4.

Matematiikan laitos järjestää kotitehtävien ohjausta viikoilla 37-49 (10.9.-5.12.) salissa M9 aikoina ma 14-18, ti 14-18 ja ke 14-16.
  1. Ratkaise integroivaa tekijää käyttäen yhtälöt

    2.  

     

    a) y¢- [ y/x] = [ 1/lnx].

    b) y¢+ (y+1)sinx = 0.

  2. Ratkaise vakion varioinnilla yhtälö
    3. y¢+ 2xy = 4e-x2.
  3. Ratkaise sopivaa polynomiyritettä käyttäen alkuarvotehtävä
    4. y¢+ 2y = x-3,     y(1) = 2.
    (Vihje: Jos yo. yhtälöllä on polynomiratkaisu, sen asteen voi päätellä suoraan yhtälöstä. )
  4. Ratkaise differentiaaliyhtälöt (a, k, a vakioita)

    5.  

     

    a) y¢ = -aty,    b) x¢ = k xa,    c) y = (1-x)y¢-1.

  5. Ratkaise separoimalla differentiaaliyhtälöt

    6.  

     

    a) (1 + x2) y¢- 1 - y2 = 0

    b) x(1-t2) x¢+ t(1-x2) = 0

  6. Ratkaise funktio y yhtälöstä y(x) = ò0x t y(t)2 dt + 1.

    7.  

     

    Vihje: Muodosta alkuarvotehtävä ja ratkaise se.

  7. (vrt. Luvun 1.3 tehtävät 4 ja 5) Oletetaan, että eristetyn populaation kasvunopeus riippuu vain populaation määrästä P = P(t), ts. P¢(t) = f(P(t)). Määritä populaation määrä hetkellä t ³ 0, kun P(0) = P0 ja

    8.  

     

    a) f(P) : = k P, missä k > 0 on (syntyvyys)vakio.

    b) f(P) : = (1- [ P/N])k P, missä k > 0 on kuten yllä ja N >   > 0 on populaation ehdoton yläraja.

    c) Miten populaation määrä käyttäytyy näissä malleissa, kun t ® ¥?

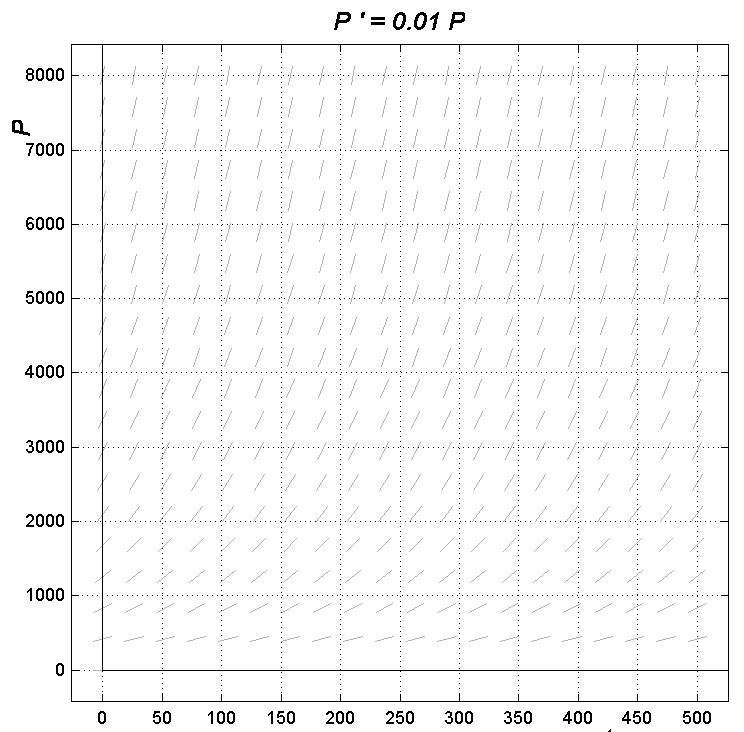
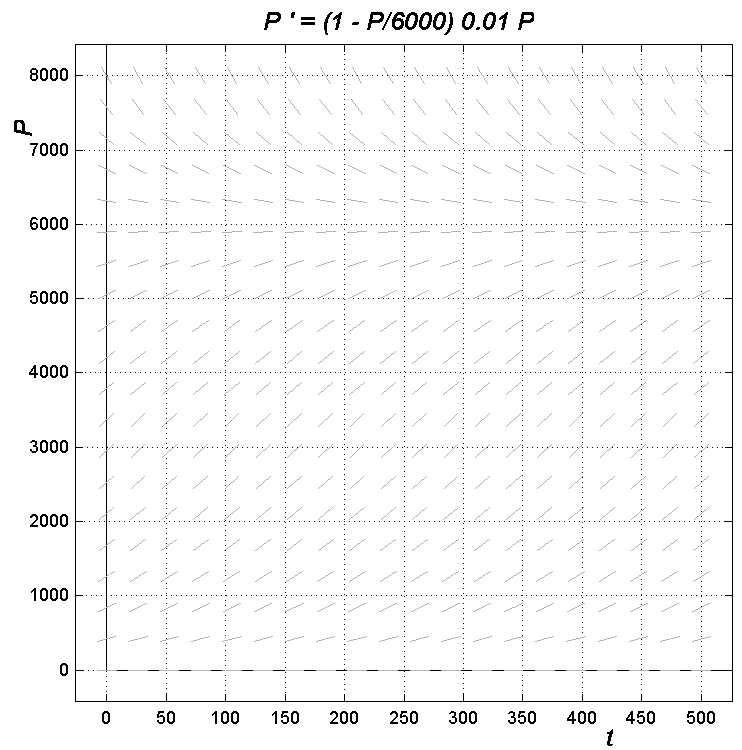
  8. Alla on kuviot tehtävän 7 molemmista tilanteista arvoilla k = 0.01 ja N = 6000.

    9.  

     

    a) Jos populaation määrä oli alussa 1000, niin paljonko se on näissä malleissa 50, 100 ja 200 aikayksikön päästä? Arvioi kuviosta sekä laske tehtävän 7 tuloksesi mukaan.

    b) Kuinka P¢ muuttuu ajan mukana?
    DYKuv01/K05018a.png
    		DYKuv01/K05018b.png

File translated from TEX by TTH, version 3.01.
On 3 Oct 2001, 11:40.