Diskreetti matematiikka, syksy 2010
Harjoitus 1 (vk. 37, 16.-17.9. to 16-18 M107, pe 12-14 M107)

Tietoa kurssista kurssin pääsivulla
http://www.joensuu.fi/matematiikka/kurssit/Diskreetti/index.html
  1. Olkoot A, B, C, D ÍE. Esitä Venn-diagrammeina joukot
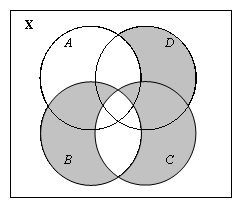
    2. a) [`(A)]Ç[`(B)]Ç[`(C)]Ç[`(D)] b) (AÇD)\C
    c) (DÇC)È(BÇC)\A d) [`(AÈBÈCÈD)] 
  2. Mitä joukkoa esittää seuraavan Venn-diagrammin harmaa alue?
    3. DM0801_2.png
  3. Osoita, että luku 11n-4n on jaollinen luvulla 7 kaikilla n ÎN.
  4. Osoita, että on olemassa n0 ÎN siten, että 2n ³n2 kaikilla n ³n0.
  5. Mitkä seuraavista ovat mielestäsi logiikan lauseita ja mitkä totuusarvot niillä on?
    6. a) "Positiivisen luvun neliö on positiivinen."
    b) "Jokaista x Î R kohti on olemassa y Î N, joille x+y > 2."
    c) "On olemassa sellainen y Î N, että jokaiselle x Î R pätee x+y > 2.
  6. Olkoot
    7. P: "Katselen televisiota.",
    Q: "Ratkaisen matematiikan kotitehtävät." ja
    R: "Opin matematiikkaa.".
    Ilmaise sanallisesti lauseet
  7. Kaverukset ovat sopineet muutamille lauseille lyhenteet:
    8. K: "Vietetään iltaa piilomajalla."
    L: "Mennään pyörällä."
    M: "Pelataan jalkapalloa kirkon takana."
    N: "Mennään uimaan Linnunlahdelle."
    O: "Mennään uimaan Aavarannalle."
    He jättävät joskus toisilleen viestejä "salakirjoituksella", jossa he yhdistelevät yllä olevia lauseita loogisia konnektiiveja käyttäen. Mitä tarkoittavat koodit
    a) K ÙL
    b) (\lnot K) ÞM
    c) (\lnot K) Þ((NÚO)ÙM) 
  8. Todista, että implikaatio voidaan esittää negaation ja disjunktion avulla muodossa
    9. PÞQº (\lnot P)ÚQ.
    Tämä onnistuu näyttämällä totuusarvotaulukolla tautologiaksi lause
    PÞQÛ(\lnot P)ÚQ
    (tai että lauseiden P ÞQ ja (\lnot P)ÚQ totuusarvosarakkeet ovat identtiset).
File translated from TEX by TTH, version 3.80.
On 05 Sep 2010, 14:46.