Diskreetti matematiikka, syksy 2010
Harjoitus 2 (23.-24.9., to 16-18 M107, pe 12-14 M107)

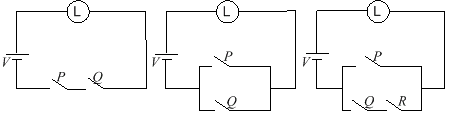
  1. Seuraavassa on kuvattu kolme virtapiiriä, joissa on paristo, sopiva lamppu L ja katkaisimia P, Q, R, joiden läpi virta kulkee (1) tai ei kulje (0). Lampun palaminen (1) riippuu katkaisimien asennoista logiikan sääntöjen mukaan.
    2. a) Muodosta kustakin piiristä "totuusarvotaulukko", josta näkyy millä kytkinten yhdistelmillä lamppu palaa ja millä ei.
    b) Mitkä logiikan yhdistetyt lauseet kuvaavat piirejä?
    kuvat/Piirit.png
  2. Millä reaaliluvuilla x on tosi lausefunktio
    3. P(x): x2 - x ³ 2(x-5)?
  3. Olkoot lausefunktiot P(x), Q(x) ja R(x) määritelty kokonaislukujen joukossa Z:
    4. P(x): |x| £ 3
    Q(x): x2 + 4 > 2
    R(x): 2x2 - x < 28
    Osoita, että P(x) º R(x), mutta P(x) \not º Q(x).
  4. Muodosta kaksipaikkaisesta lausefunktiosta
    5. P(x,y): x2 - y2 = 2
    kaikki erilaiset kvanttorien avulla saaatavat lauseet sekä määritä niiden totuusarvot.
  5. Esitä suora todistus ja epäsuora todistus väitteelle:
    6. "Jos m on parillinen ja n pariton kokonaisluku, niin m+n on pariton luku."
    Opastusta: On useita tapoja, voidaan johtaa ristiriita oletuksen tai yhtä hyvin jonkin ulkoisen totuuden kanssa. Oletetaan tässä tunnetuksi seuraavat ulkoiset totuudet U ja V:
    U: "Kokonaisluku n on parillinen, jos ja vain jos on olemassa kokonaisluku p, jolle n = 2p."
    V: "Kokonaisluku n on pariton, jos ja vain jos on olemassa kokonaisluku p, jolle n = 2p+1."
  6. Olkoot P: "Katselen televisiota."
    7. Q: "Ratkaisen matematiikan kotitehtävät."
    R: "Opin matematiikkaa.".
    Onko seuraava päättely johdonmukainen?
    Katselen televisiota tai ratkaisen matematiikan kotitehtävät. Jos katselen televisiota, en opi matematiikkaa. Jos ratkaisen matematiikan kotitehtävät, en katsele televisiota. Siis opin matematiikkaa.
    Mietipä ensin sillä terveellä talonpoikaisjärjellä (mistähän sitäkin saa?), tuntuuko päättely vedenpitävältä! Ratkaise sitten tehtävä Esimerkin 2.3.8 mallin mukaan: Pue päättely jonoksi, jossa esiintyvät annetut (kolme) premissiä ja johtopäätös. Muodosta totuusarvotaulukko. Vaikeinta lienee sitten taulukon tulkitseminen!
  7. Näin ajateltiin jokunen vuosikymmen sitten:
    8. Jos ihmisen geenikartat tulevaisuudessa selvitetään, niin on mahdollista, että ihmisen perimää voidaan säädellä. Ihmisen geenikartat saadaan tulevaisuudessa selville tai biologian kehitys pysähtyy. Mutta biologian kehitys jatkuu. Siis ihmisen perimää voitaneen tulevaisuudessa säädellä.
    Oliko johdonmukaisesti päätelty?
  8. Tarkastellaan lopuksi nk. logiikkaportteja (logiikka « digitaalitekniikka, Claude Shannon 1938). Kun merkitsemme Tosi = 1 ja Epätosi = 0, saadaan vastaavuudet:
    9. Kombinatoriset eli loogiset piirit ovat elektronisia systeemejä, joilla toteutetaan totuusfunktioita syöttämällä piiriin muuttujien arvot jännitetasoina (esim. 1 = 5 V ja 0 = 0V) ja tuloksena saadaan funktion arvoa vastaava jännite (joka voidaan edelleen syöttää muille piireille). Siis
    kuvat/KombinatorinenPiiri.png
    Loogiset piirit rakennetaan porteista, joita ovat loogiset perusoperaatiot Ù, Ú ja \lnot eli AND, OR ja NOT. Lisäksi on portit operaatioille NAND, NOR ja XOR. Perusporttien piirrosmerkit ovat
    kuvat/LoogisetPerusportit.png
    Osoita, että AND-, OR- ja NOT-porteilla voidaan toteuttaa myös portit NAND, NOR ja XOR,
    kuvat/LoogisetPerusportitMuut.png
    missä xÑy on toisensa poissulkeva "tai", siis "joko tai".

File translated from TEX by TTH, version 3.80.
On 14 Sep 2010, 15:38.