Diskreetti matematiikka, syksy 2010
Harjoitus 9 (pe 19.11. klo 12-14 M107)
Torstaina 18.11. olemme klo 16-18 tietokoneluokassa MP103. Teemme Matlab-demoa 3.

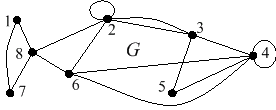
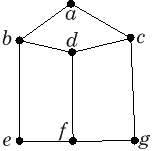
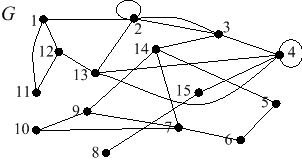
  1. Määritä alla olevasta verkosta G seuraavat asiat:
    2. a) solmujoukon {1, 2, 3, 4, 6, 7} virittämä aliverkko G¢.
    b) aliverkon G¢ yhtenäiset komponentit, sekä piirrä tilanteista kaavioesitys.
    DM1004_02.png

     
  2. Muodosta tehtävän 1 verkkojen G ja G¢ yhteysmatriisit.

    3.  
  3. Todista Lause 12.5.4: Olkoon G = (X, E, Y) äärellinen suuntaamaton verkko, x, y ÎX ja c ketju x® y. Osoita, että verkossa G on yksinkertainen ketju x®y, joka voidaan valita niin, että se sisältää vain ketjun c kaaria.

    4.  
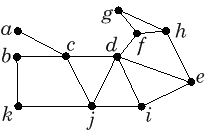
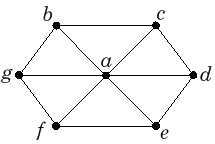
  4. Suuntaamattoman verkon kaari on silta, jos sen poistaminen epäyhtenäistää verkon (tai oikeastaan sen yhtenäisen komponentin, johon kaari kuului).
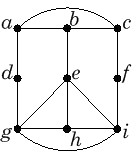
    5. a) Määritä seuraavan verkon yhtenäiset komponentit:
    DM1104_01.png
    b) Jos löydät sillan, poista se ja määritä sitten jäljellä olevan verkon G¢ yhtenäiset komponentit.

     
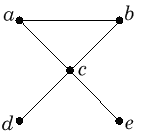
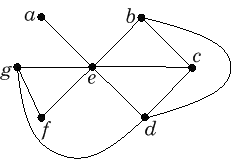
  5. Onko seuraavissa verkoissa avoimia ja/tai suljettuja Hamiltonin ketjuja?
    6. Jos on, etsi yksi sellainen, muutoin perustele kantasi.
    a) DM1104_2A.png b) DM1104_2B.png c) DM1104_2C.png d) DM1104_2D.png

     
  6. Selvitä piirroksin ja "kirjanpidolla", miten etenee tehtävän 5 verkossa a)
    7. a) syvyyshaku- eli depth-first-menetelmä.
    b) leveyshaku- eli breadth-first-menetelmä.
    Valinnaistilanteissa valitse solmu joka on aakkosjärjestyksessä ensin.

     
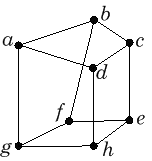
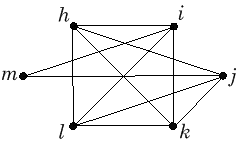
  7. Onko seuraavissa verkoissa avoin ja/tai suljettu Eulerin ketju? Jos on, etsi yksi sellainen, muutoin perustele kantasi.
    8. a)DM1104_4A.png b)DM1104_4B.png
    c)DM1104_4C.png d)DM1104_4D.png
File translated from TEX by TTH, version 3.33.
On 09 Nov 2010, 14:12.