1. Alkutoimet
1.1. Luokat, koneet ja hakemistoasiaa
Kurssin harjoitustehtäviä ja -töitä voi
tehdä ainakin luokissa M17, M18 ja M15 silloin, kun ne eivät
ole muuhun toimintaan varattuja. Näissä luokissa kirjaudutaan
tietokoneverkkoon samalla tavalla: tarvitaan käyttäjätunnus
ja salasana, jotka kaikilla opiskelijoilla pitäisi olla tiedossaan.
Matlab 5.3 (release 11) on asennettuna näihin koneisiin.
Kullakin käyttäjällä lienee palvelimella
cc
tai cs oma kotihakemisto X:,
johon voi tallettaa pienen määrän tiedostoja.
Kotihakemistona voi olla myös levykeasema A:
(tai zip-asema, ei kuitenkaan M15:ssä).
Joka tapauksessa myös käytettäessä
X:-asemaa
työskentelyyn pitää tiedostoista olla varalta - ja mieluiten
työskentelykelpoinen - kopio levykeellä!
Kotihakemiston "juureen" tehdään kurssin tiedostoja
varten seuraava hakemistorakenne:
 |
Oma X:-asemasi tunnus voi tietenkin
näyttää toisenlaiselle.
Hakemistoihin lisätään tavaraa pikkuhiljaa.
Aluksi niihin laitetaan vain perustyökalut kuten
- hakemistoissa liikkumista helpottavat komentojonot
- opastustiedostoja
- funktioita erityisten satunnaismatriisien luomiseksi
- piirtofunktioita |
1.2. Tiedostot alkutilanteessa
Tähän listataan alussa jaettavat tiedostot:
| DISKREET |
|
|
|
|
|
|
|
LUKUMAAR |
REKURSIO |
RELAATIO |
VERKOT
|
|
|
|
|
SUUNTAAM |
SUUNNATT |
PAINOTET |
luveppa_tua.txt
alustus.m
diskr.m
luk.m
rek.m
rel.m
verk.m
ston.m
sttu.m
pain.m
yleista.m
editori.m
funktiot.m
toisto.m
talletus.m |
|
|
tarkastu.m
piirrel1.m
piirrel2.m
piiralk1.m
piiralk2.m
piirnuo1.m
piirnuo2.m
satrel.m |
|
|
|
Tiedostot annetaan zipattuina, jolloin ensimmäisissä
demoissa tehdään seuraavasti:
1) luodaan X:lle hakemisto diskreet
2) napataan sinne Kurssimateriaalia-sivulta kyseinen
DISKREET.ZIP
3) puretaan se kyseiseen hakemistoon vaikkapa Winzip-ohjelmalla
pitäen huolta, että myös alihakemistot (subfolders) tulevat
mukaan. Näin hakemistorakenne tulee (toivottavasti) suoraan kuntoon!
2. Matlabin käytöstä
2.1. Yleistä
MATLAB on tunnettu, laajalti teknillisessä ja tieteellisessä
laskennassa käytetty kaupallinen ohjelma,
joka on parhaimmillaan numeerisessa matriisipohjaisessa
laskennassa sekä grafiikassa.
Matlabissa työskennellään yleensä
"interaktiivisesti" tulkkipohjalta,
ts. ohjelman ollessa käynnissä sille annetaan
"selväkielisiä" käskyjä ja odotetaan "vastaus".
2.2. Matlabin käynnistys ja ensimaistiaiset
| Matlab käynnistetään normaaliin Windows-tapaan
pikakuvakkeella tai Käynnistä-valikon kautta. Matlabin käynnistyksen
jälkeen olemme komentoikkunassa, (command window). jossa lukee
To
get started, type one of these: helpwin, helpdesk, or demo.
For product information,
type tour or visit www.mathworks.com.
»
Valmiusmerkin »
perään voi alkaa kirjoittaa käskyä tai useitakin, kunhan
erottaa ne pilkulla tai puolipisteellä. Matlabista poistuttaisiin
komennolla quit tai exit:
» exit |
 |
Muita ikkunoita aukeaa sitten, kun piirretään tai
halutaan editoida tiedostoja.
Tarvittaessa Matlabia voi käyttää pelkkänä
laskimena, funktiolaskimena ja piirtovälineenä.
Esimerkki 2.2.1. Aritmetiikkaa:
» 16/8
ans =
2
» 16/9
ans =
1.7778
» 2*4 + 3*(5-2)/3
ans =
11
» 3*sin(2.3*pi)
ans =
2.4271 |
Matlab yrittää laskea kokonaisluvuilla, jos
syötteet ja ovat niitä.
Kertomerkki pitää kirjoittaa.
Samoin desimaalipiste. Vakio pii on pi. |
Yleensä työskentelyssä kannattaa käyttää
apuna muuttujia. Lisäksi kannattaa kirjoittaa kommentteja
(ainakin jälkikäteen ja tiedostoihin) helpottamaan
ohjelman lukemista
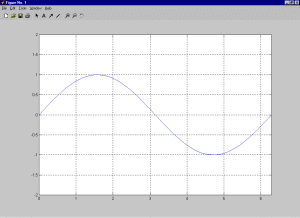
| Esimerkki
2.2.2. Käyrän piirto
» x = 0:0.1:10;
% pisteikkövektori [0 0.1 0.2 etc ]
» y = sin(x);
% sini kustakin
» length(y)
% tulosvektorin pituus
ans =
101
» plot(x,y)
% piirto (Figure-ikkunaan)
» axis([0 2*pi -2 2]) % akselien
automatiikan ylitys
» grid
% vielä ruudukko |
 |
Matlabin matemaattisia funktioita
abs
absolute value or complex magnitude
angle phase angle
sqrt square
root
real real
part
imag imaginary
part
conj complex
conjugate
round round to
nearest integer
fix
round toward zero
floor round toward
-infinity
ceil round
toward infinity
sign signum
function
rem
remainder
exp
exponential base e
log
natural logarithm
log10 log base
10
2.3. Erikoismerkit ja arvot
Matlabissa joillekin kummallisille symboleille on annettu
erikoismerkitykset, joista joihinkin olemme jo tutustuneetkin
=
assignment statement
[
used to form vectors and matrices
]
see [
(
arithmetic expression precedence
)
see (
.
decimal point
...
continue statement to next line
,
separate subscripts and function arguments
;
end rows, suppress printing
%
comments
:
subscripting, vector generation
!
execute operating system command
Samoin on joitakin ennalta määrättyjä
arvoja
ans
answer when expression not assigned
eps
floating point precision
pi
pi
i, j sqrt(-1)
inf
infinity
NaN
Not-a-Number
clock wall clock
date date
flops floating
point operation count
nargin number of function
input arguments
nargout number of function
output arguments
2.4. Peruskäskyjä
Seuraavassa kokoelma peruskäskyjä:
| YLEISLUONTOISIA MATLAB-KÄSKYJÄ |
TIEDOSTOJEN HALLINTAAN YM |
help apuva
lookfor etsii merkkijonoja
who muistissa olevat
muuttujat
what listaa M-tiedostot
which paikantaa funktioita ja tiedostoja
path näyttää
määritellyt polut
addpath lisää polun alkuun tai loppuun
matlabpath ei suositella enää
clc clear command screen
clear clear workspace
computer type of computer
demo run demonstrations
home move cursor home
format set output display format
disp display matrix or text
echo enable command echoing |
cd change current directory
pwd show current working directory
delete delete file
diary diary of the session
dir directory of files on disk
load load variables from file
save save variables to file
type list function or file
what show M-files on disk
fprintf write to a file
pack compact memory via save
print send graph to printer
prtsc screen dump
^C local abort
exit exit MATLAB
quit same as exit |
Kokeillaanpa näitä:
» cd X:
» cd diskreet
» pwd
ans =
X:\diskreet
» dir
.
funktiot.m rel.m
toisto.m
..
luk.m relaatio
verk.m
alustus.m
luveppa_tua.txt ston.m
yleista.m
diskr.m
pain.m sttu.m
editori.m
rek.m talletus.m
» what
M-files in the current directory X:\diskreet
alustus funktiot
rek sttu
verk
diskr luk
rel talletus yleista
editori pain
ston toisto
» alustus
» path
Tämä näyttää polut, joista Matlab
etsii järjestyksessä M-tiedostoa, jos se ei ole nykyisessä
hakemistossa.
Nyky-Matlab antaa hyvät mahdollisuudet etsiä
tietoa, jos vain käyttäjätkin kirjoittaisivat M-tiedostoihinsa
sopivasti informaatiota esim. kommenteiksi.
» lookfor satun
SATREL.M: %Satunnaisrelaatioita: function M =
satrel(n, m, prosenttia);
paljastaa, että merkkijono satun
esiintyy ainakin M-tiedostossa SATREL.M sen ensimmäisellä kommenttirivillä!
Mitäs antaakaan
» help satrel
Satunnaisrelaatioita: function M = satrel(n,
m, prosenttia);
missä
n, m = matriisin rivien
ja sarakkeiden määrät
prosenttia = optionaalinen, jos esiintyy,
tulkitaan
ykkösten prosentuaaliseksi
osuudeksi (oletusarvo 50 %)
Muodostaa nxm-satunnaisrelaation matriisin
M.
Koeta vielä
» help diskreet
Huomautus! On syytä
jo tässä korostaa, että vaikka tehty työ jääkin
ikkunaan näkyviin,
on aktiivisena ainoastaan viimeisellä
rivillä valmiusmerkin » jälkeinen
alue.
Tälle riville voi siirtää
kopioiden ja liimaten Matlab-käskyjä, jopa useita rivejä.
Kokeillen havaitsee miten pitää
toimia, tai ainakin miten ei!
Esimerkki 2.3.1. Käskyllä
rand
luodaan satunnaismatriiseja:
» M = rand(3,4)
M =
0.9501
0.4860 0.4565 0.4447
0.2311
0.8913 0.0185 0.6154
0.6068
0.7621 0.8214 0.7919 |
Tehtävä
2.3.1. Mitä tulostaa seuraava jono?
I = eye(4,4);
S = sum(I);
sum(S)
diag(S) |
Monisteen luvussa 1.2 määritellään
relaatio ja puhutaan sen matriisiesityksestä. Askartelun luistamiseksi
opettelemme
"arpomaan" satunnaisia relaatioiden matriiseja (oleellisesti
funktion SATREL toiminta).
Tilan säästämiseksi tässä on
tyydytty pienikokoisiin matriiseihin
Esimerkki 2.3.2. Tässä arvotaan 0-1
matriisi,
jossa on n. 70 % ykkösiä (ja vielä lasketaan
jotain).
» M = (rand(5,5)
> 0.3)
M =
0 0 1
0 1
1 1 1
1 1
1 1 1
1 1
0 0 1
0 0
1 1 1
1 1
» sum(M)
ans =
3 3 5
3 4
» sum(M')
ans =
2 5 5
1 5 |
Tehtävä 2.3.2. Oletetaan, että
Esimerkin matriisi M
on
joukon X x Y relaation R matriisi.
Mitä ohessa ilmaisevat arvot ans
kyseisestä relaatiosta?
Ensimmäinen ans:
Toinen ans:
|
Seuraavat kuviot on piirretty hakemiston RELAATIO ohjelmilla
PIIRREL2
ja PIIRREL:
» piirrel2(M)
» piirrel(M)
 |
 |
| PIIRREL2 silloin kun on eri joukot X ja Y |
PIIRREL vain kun X = Y. |
Sovitaan, että kurssilla pyritään käyttämään
omille
funktioille suomenkieltä muistuttavia nimiä, erotukseksi
Matlabin omista englanninkieltä muistuttavista nimistä. Koska
toisaalta tiedostojen nimet pyritään varovaisuussyistä pitämään
enintään 8 merkin mittaisina,
johtaa kuvaavien nimien (usein yhdyssanoja) joskus aika
erikoiseen ratkaisuus (SATREL).
Pyydän käyttämään
luovuutta aivan omissa ratkaisuissanne, paitsi kun kun käytetään
yhteisiä tiedostoja!
3. Lukumatriisien ja vektorien operaatioita
Tällä kurssilla tarvitsemme operoida kokonaislukumatriisella
ja logiikkamatriiseilla. Aluksi käskyjä
Matriisien luontiin ja tutkimiseen
size row and column dimensions
length vector length
diag diagonal
eye identity
ones constant
zeros zero
magic magic square
rand random elements
reshape reshape
: convert
matrix to single column; A(:)
3.1. Aritmeettiset operaatiot
Matriiseilla voi laskea yleensä kahdella tavalla, alkioittain
tai "oikeasti", kuten matriisien kertolaskut ja jakolaskut:
Matrix Operators
Array Operators
---------------------------------------------------
+ addition
+ addition
- subtraction
- subtraction
* multiplication
.* multiplication
/ right division
./ right division
\ left division
.\ left division
^ power
.^ power
' conjugate transpose
.' transpose
Esimerkkejä
3.2. Funktioiden kohdistaminen matriiseihin
Lukuihin kohdistuvat funktiot toimivat myös kohdistettuina
vektoreihin tai matriiseihin (vrt. sin(x) edellä).
Tähän esimerkkejä!
4. Loogiset operaatiot
Matlabissa on valmiina
Logiikan operaatiot
~ negaatio
& ja
| tai
Muuthan voidaan esittää näiden avulla.
Loogiikka-arvoja 0/1 saadaan vertailuoperaatioiden tuloksena
Vertailuoperaatiot
<
less than
<=
less than or equal
>
greater than
>=
greater than or equal
==
equal
~=
not equal
Etsintää
any logical conditions
all logical conditions
find find array indices
of logical values
isempty detect empty matrices
isnan detect NaNs
finite detect infinities
Aina ei kuitenkaan ole selvää, ovatko 0 ja 1
lukuja vai totuusarvoja.
» v = round(10*rand(1,10))
v =
3 2
0 7 4
9 5 4
8 5
» S5 = v > 5
S5 =
0 0
0 1 0
1 0 0
1 0
» v(S5)
ans =
7 9
8
Mutta:
» I = [1 0 1 1 0 1 1 1 1 1]
I =
1 0
1 1 0
1 1 1
1 1
» v(I)
??? Index into matrix is negative or zero. See release notes
on changes to
logical indices.
» L = logical(I)
L =
1 0
1 1 0
1 1 1
1 1
» v(L)
ans =
3 0
7 9 5
4 8 5
Help antaa ohjeita kuinka operaatioita tai funktiota voidaan
käyttää, usein monin eri tavoin.
Esimerkki 3.1.1
» help find
antaa pitkän listan käyttötapoja.
» [I,J] = find(N);
» I',J'
ans =
1 3 2
3 3 2
3
ans =
1 1 2
2 3 4
4 |
Tehtävä 3.1. Kokeile vielä mitä tekevät
seuraavat kolme käskyä
» ~N, N & ~N,
N | ~N
ja selvitä merkkien ~, &, | vaikutus Matlab-käskyinä. |
5. Merkkijonoista
Matlabissa merkkijono on tavallaan vektori, sillä on
pituus, merkeillä asemansa (indeksinsä) ja merkkejä voidaan
paikantaa niiden mukaan.
» MJ = 'Diskreetti matematiikka'
» MJ =
Diskreetti matematiikka
» K = 'a';
» indik = (MJ == K)
indik =
Columns 1 through 12
0 0
0 0 0
0 0 0
0 0 0
0
Columns 13 through 23
1 0
0 0 1
0 0 0
0 0 1
» aat = MJ(indik)
aat =
aaa
» length(aat)
ans =
3 |
|
» sum(indik)
ans =
3
» disp(['Jonossa ''',MJ,''' on ',int2str(sum(MJ == K)),'
',K,'-kirjainta.'])
Jonossa 'Diskreetti matematiikka' on 3 a-kirjainta. |
|
Merkkijonojen käsittelyä
abs
convert string to ASCII values
eval evaluate
text macro
num2str convert number to
string
int2str convert integer to
string
setstr set flag indicating
matrix is a string
sprintf convert number to
string
isstr detect string
variables
strcomp compare string variables
hex2num convert hex string
to number
6. Ohjelmointia
Matlabissa on oma suppeahko, selkeä ohjelmointikielensä,
jota oppii nopeasti käyttämään.
Kielen perusobjekteja ovat
| muuttujat |
merkkijono, looginen 0-1-matriisi ja numeerinen matriisi |
| operaattorit |
loogiset ja numeeriset laskutoimitukset |
| funktiot |
sisäänrakennetut ja valmiit M-tiedostofunktiot |
| toisto- ja ehtorakenteet |
for - ja
while-silmukat
sekä
if-else - ehtolause |
joita käyttäen on helppo muodostaa ohjelmia.
Seuraava taulukko sisältää
Ohjauskäskyjä ohjelmointiin
if
conditionally execute statements
elseif used with if
else used
with if
end
terminate bif, for, while
for
repeat statements a number of times
while do while
break break out
of for and while loops
return return from functions
pause pause until
key pressed
Omia pikkuohjelmia voi tehdä myös suoraan komentoikkunassa:
mutta yleensä ohjelmat ja funktiot kannattaa tallettaa
korjailua ja myöhempää käyttöä varten nk.
M-tiedostoiksi.
Tällä kurssilla noita M-tiedostofunktioita
laaditaan runsaasti, tarkoituksena rakentaa "työkalupakki" diskreetin
matematiikan objektien kuten relaatioiden ja verkkojen tutkimiseksi.
4.1. M-tiedostot
Matlabin M-tiedostot ovat tekstitiedostoja, jotka voivat
olla komentojonoja, funktioita tai dataa sisältäviä.
Funktiot voivat kutsua toisiaan ja olla rekursiivisia,
ts. kutsua itseään.
Matriisien käsittelyä varten MATLABissa on
monipuolinen kokoelma
standardifunktioita, joilla käytännön
laskutyö sujuu mutkattomasti.
MATLABilla työskentelevästä näyttääkin
siltä, kuin
elettäisiin vektoroidussa ympäristössä.
input
get numbers from keyboard
keyboard call keyboard
as M-file
error
display error message
function define function
eval
interpret text in variables
feval
evaluate function given by string
echo
enable command echoing
exist
check if variables exist
casesen set
case sensitivity
global
define global variables
startup startup
M-file
getenv
get environment string
menu
select item from menu
etime
elapsed time
Kunkin ohjelman kommenttiriveiltä, jotka alkavat
%-merkillä, selviävät funktion suorittama tehtävä,
tarvittavat syöttötiedot ja funktion mahdollisesti palauttamien
olioiden merkitys. Lisäksi on lueteltu ohjelman käyttämät
omat alifunktiot.
Funktion pääasiallinen INPUT on matriisi; lisäksi
voi olla muita parametreja, joista osa on optionaalisia.
Matlabissa siirrytään hakemistoon DISKREET,
jossa ajetaan komentojono ALUSTUS
>> alustus
joka lataa tarvittavat polkumääritykset.
Varsinaisia diskreetin matematiikan funktioita käytetään
siinä hakemistossa, jossa ne sijaitsevat.
Hakemistoissa liikutaan lyhenteillä
diskr rel verk sttu ston pain luk rek
DISKREET-hakemistossa on erityisohjeita MATLABin käyttöä
varten, mm. vain kommenttirivejä sisältävät funktiot
yleista editori funktiot toisto ja talletus
Funktion kommenttirivit saa MATLABista käsin näkyviin
käskyllä help funktio
>> help yleista (enter)
>> help piirrel (enter)
Lisäksi kannattaa käyttää käskyjä
dir, type, who, what, joilla saa
hakemiston listauksen, tiedoston listauksen,
käytössä olevien muuttujien ja funktioiden
listan.
Huomaa, että isot ja pienet kirjaimet ovat MATLAB-komentoina
eri asia!
7. Grafiikasta
Grafiikkaa kurssilla käytetään pääasiassa
kurssia varten ohjelmoitujen funktioiden avulla.
Tässä kuitenkin piirtokäskyjä:
plot
linear X-Y plot
loglog
loglog X-Y plot
semilogx semi-log
X-Y plot
semilogy semi-log
X-Y plot
polar
polar plot
mesh
3-dimensional mesh surface
contour contour
plot
meshdom domain
for mesh plots
bar
bar charts
stairs
stairstep graph
errorbar add error
bars
Graph Annotation
title
plot title
xlabel
x-axis label
ylabel
y-axis label
grid
draw grid lines
text
arbitrarily position text
gtext
mouse-positioned text
ginput
graphics input
Graph Window Control
axis
manual axis scaling
hold
hold plot on screen
shg
show graph window
clg
clear graph window
subplot split
graph window





