1.5  Moivre'n kaava.

Olkoon z = r(cosj+ i sinj). Silloin

zn = rn(cosnj + i sinnj).
Jos valitaan r = 1, jolloin z = cosj+isinj, saadaan ns. Moivre'n kaava
(cosj+i sinj)n = cosnj +i sinnj.
Tämä on kätevä moninkertaisten kulmien sinien ja kosinien laskemiseen. Valitaan esim. n = 5. 

                               1
                             1   1
                           1   2   1
                        1    3   3   1
                      1    4   6   4   1
                    1   5   10   10  5   1
Kuva 8: Pascalin kolmio
(cosj+isinj)5 = cos5j+5icos4jsinj-10cos3jsin2j-10icos2jsin3j+5cosjsin4j+isin5j.
Näin ollen
cos5j
=
Re (cosj+isinj)5
=
cos5j-10cos3jsin2j+5cosjsin4j
sin5j
=
Im (cosj+isinj)5
=
sin5j-10cos2jsin3j+5cos4jsinj.
Näitä voidaan vielä muokata eri muotoihin. Sijoitetaan esimerkiksi ensimmäiseen sin2j = 1-cos2j :
cos5j
=
cos5j-10cos3j(1-cos2j)+5cosj(1-cos2j)2
=
cos5j-10cos3j+10cos5j+5cosj(1-2cos2j+cos4j)
=
16 cos5j-20cos3j+5cosj.

Vastaavasti

cos3j
=
Re (cosj+isinj)3
=
Re (cos3j+3icos2jsinj-3cosjsin2j-isin3j)
=
cos3j-3cosjsin2j
=
cos3j-3cosj(1-cos2j)
=
4cos3j-3cosj.
Tästä seuraa esimerkiksi kaava
cos3j = 1
4
 cos3j+ 3
4
 cosj.
Unohtuneet kaavat on helppo johtaa:
Koska
cos2j+isin2j
=
(cosj+isinj)2
=
cos2j+2isinjcosj-sin2j
on
cos2j
=
cos2j-sin2j,
sin2j
=
2sinjcosj.

1.6  Eulerin kaava.

Jos x Î R, niin

ex
=
1+x+ x2
2!
 + x3
3!
 + x4
4!
 + ¼
cosx
=
1- x2
2!
 + x4
4!
 - x6
6!
 + ¼
sinx
=
x- x3
3!
 + x5
5!
 - x7
7!
 + ¼.
Toisaalta
i1
=
i
i2
=
-1
i3
=
-i
i4
=
1
i5
=
i
i6
=
-1
i7
=
-i
jne.
Sijoitetaan ex:n sarjakehitelmään x = ij. Silloin
eij
=
1+ij- j2
2!
 -i j3
3!
 + j4
4!
 +i j5
5!
 - j6
6!
 -i j7
7!
 + ¼
=
cosj+isinj,
joten olemme saaneet ns. Eulerin kaavan
eij = cosj+isinj.
Tämän perusteella kompleksiluvuilla z, argz = j, |z| = r, on esitys
z = reij.
Moivren kaava saa muodon
(eij)n = einj.

1.7  Esimerkkejä.

1. Laske (1+iÖ3)6 Moivren kaavan avulla. Kuvan 9 perusteella on

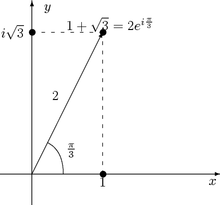
Kuva 9:
(1+iÖ3)6 = 26ei[(6 p)/3] = 26e2pi = 64.

2. Ratkaise yhtälö z3 = 1.
Merkitään z = reij. Silloin z3 = r3e3ij. Koska |e3ij | = 1, on

|z|3
=
r3 | e3ij | = r3 = 1 Û r = 1.
z3 = 1
Û
r = 1  ja  e3ij = 1 = en2pi, n = 0,±1,±2,... .
z3 = 1
Û
j = n 2
3
 p, n = 0,±1,±2,... .

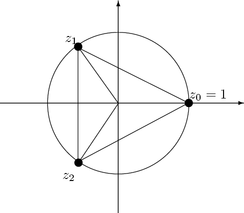Kuva 10: Yhtälön z3 = 1 ratkaisut
z1
=
cos120°+isin120° = - 1
2
 +i Ö3
2
z2
=
z1
 
 = - 1
2
 -i Ö3
2
 .
Tarkastus:
z13 = (- 1
2
 +i Ö3
2
 )3
=
- 1
8
 +3i 1
4
 · Ö3
2
 + 3 1
2
 · 3
4
 -i( Ö3
2
 )3
=
9
8
 - 1
8
 = 1
z23 = (
z1
 
 )3
=
(z13)
 
 =
1
 
 = 1.

Yleisesti ottaen binomiyhtälön

zn = 1
juuret ovat yksikköympyrän kehällä. Ne sijaitsevat säännöllisen n-kulmion kärjissä, jonka yksi kärki on pisteessä 1.

3. Ratkaise yhtälö z4 = 1.
Piirretään yksikköympyrä ja sen sisään neliö, jonka yksi kärki on pisteessä z = 1.

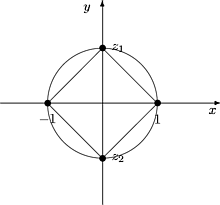Kuva 11: Yhtälön z4 = 1 ratkaisut

Juuret ovat neliön kärjissä:

z1
=
1
z2
=
i
z3
=
-1
z4
=
-i.

4. Laske eip.

eip = cosp+isinp = -1.

1.8  Binomiyhtälö

Yleisellä binomiyhtälöllä tarkoitetaan yhtälöä

zn = w,
missä z on tuntematon ja w annettu kompleksiluku. Edellä käsiteltiin muotoa
zn = 1
(1)
olevia erikoistapauksia. Jos merkitään z = reij, saadaan (1) muotoon
rn ei nj = 1 Û ì
í
î
r
= 1
nj
= k2p.
Yhtälön (1) juuret ovat siis
zk: ì
ï
ï
í
ï
ï
î
r
= 1
j
= k 2p
n
 , k = 0,±1,±2,¼.
Kun k = 0, saadaan triviaali juuri z0 = 1.
Kun k = 1, saadaan niin sanottu n:s yksikköjuuri
z1 = ei[(2p)/(n)] = cos 2p
n
 +isin 2p
n
 ,
jolle käytetään merkintää en. Koska
enk = eik[(2p)/(n)] = zk,
voidaan muut (1):n juuret esittää en:n potensseina, ja kaikki en:n potenssit ovat (1):n juuria.

Yhtälöllä (1) on täsmälleen niin monta juurta kuin en:llä on eri potenssia. Nämä ovat

en0
=
1
en1
=
en
en2
:
enn-1
sillä
enn
=
ei n[(2p)/(n)] = e2pi = 1
enn+1
=
en
enn+2
=
en2  jne.
(Kun lasketaan luvuilla enk, joiden moduli =1, on kertolasku pelkkää argumenttien yhteenlaskua.)
Binomiyhtälöllä (1) on täsmälleen n kpl eri juurta. Nämä sijaitsevat kompleksitasossa sen säännöllisen n-kulmion kärjissä, jonka yksi kärki on pisteessä z = 1 ja keskipiste on origossa (Kuva 12).

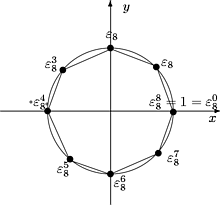Kuva 12: Yhtälön z8 = 1 ratkaisut

Esimerkki. Olkoon a yhtälön

1+z+z2+z3+z4 = 0
(2)
juuri. Osoita, että myös a2 on yhtälön juuri.
Ratkaisu: Koska
1-z5 = (1-z)(1+z+z2+z3+ z4)
ja z = 1 ei ole (2):n juuri, on
1+z+z2+z3+z4 = 0 Û z5 = 1, z ¹ 1.
Näin ollen a = e5k jollakin k = 1,2,3,4.

Tällöin a2 ¹ 1. Toisaalta a2 = e52k on yhtälön z5 = 1 juuri. Siis a2 on (2):n juuri.

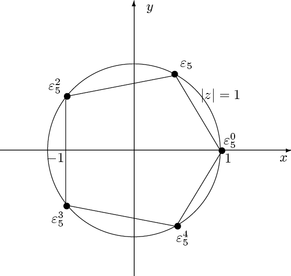Kuva 13: Yhtälön z5 = 1 ratkaisut

Sama tehtävä ei onnistu, jos astelukua nostetaan yhdellä:

(1+z+z2+z3+z4+ z5)(1-z) = 1-z6.
a = -1 on yhtälön 1+z+z2+z3+z4+ z5 = 0 juuri, mutta a2 = 1 ei ole.

Siirrymme nyt yleiseen binomiyhtälöön

zn = w = reiy,        y > 0.
(3)
Sijoituksella z = reij saadaan
rnei nj = reiy Û ì
í
î
rn
= r
nj
= y+k2p,  k = 0,±1,±2,....
Yhtälöllä (3) on juuret
zk: ì
ï
ï
ï
í
ï
ï
ï
î
r
= n æ
Ö
r
 
j
= y
n
 +k 2p
n
 ,  k = 0,±1,±2,... .
Merkitään
z0 = n æ
Ö
r
 
 ei[(y)/(n)].
Silloin muut juuret ovat
z1
=
z0en
z2
=
z0 en2
:
zn-1
=
z0 enn-1
Juuret z0,...,zn-1 sijaitsevat sen säännöllisen n-kulmion kärjissä, jonka yksi kärki on pisteessä z0 ja keskipiste on origossa (kuva ).

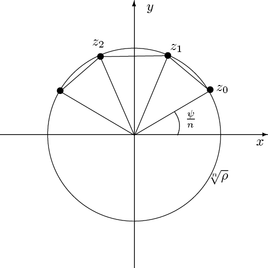Kuva 14: Yleisen binomiyhtälön juuret

Esimerkki. Yhtälön z4 = -1 = eip juuret ovat (kuva )

z0 = ei[(p)/4] = Ö2
2
 +i Ö2
2
z1
=
- Ö2
2
 +i Ö2
2
z2
=
- Ö2
2
 -i Ö2
2
z3
=
Ö2
2
 -i Ö2
2
eli z2 = -z0,   z3 = [`(z0)],  ja   z1 = -[`(z0)].

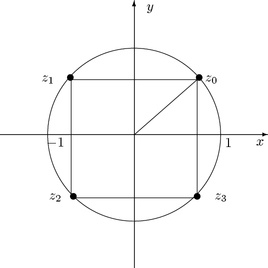Kuva 15: Yhtälön z4 = -1 juuret
File translated from TEX by TTH, version 2.32.
On 30 Sep 1999, 12:20.