3 Analyyttiset funktiot
3.1 Kompleksimuuttujan
kompleksiarvoinen funktio
Olkoot A ja B kompleksitason C osajoukkoja.
Kuvausta
sanotaan kompleksimuuttujan kompleksiarvoiseksi
funktioksi. Usein on B = C.
1.Vakiokuvaus. Esimerkiksi kuvaus f:C® C, f(z) = 1
kaikilla z Ī C on
kompleksimuuttujan kompleksiarvoinen funktio. Yleisesti olkoon
A Ģ C ja a Ī C. Silloin kuvaus f:A ® C,
on vakiofunktiona kompleksimuuttujan kompleksiarvoinen funktio.
2.Identtinen kuvaus. Olkoon A
Ģ C ja f(z) = z kaikilla
z Ī A. Silloin
f:A ® A on joukon
A identtinen kuvaus.
3. Muotoa
| S(z) = |
az+b
cz+d
|
;a,b,c,d
Ī C |
|
olevia kuvauksia sanotaan Möbius-kuvauksiksi. Jos valitaan
a = d = 1 ja b = c = 0, on
S(z) = z eli S: C® C on identtinen kuvaus. Jos
ad-bc = 0 ja |c|+|d| ¹ 0 (eli
cz+d ¹ 0), S on
vakiokuvaus: Jos c ¹ 0, on
| S(z) = |
acz+bc
c(cz+d)
|
= |
acz+ad
c(cz+d)
|
= |
a(cz+d)
c(cz+d)
|
= |
a
c
|
|
|
Jos d ¹ 0, on vastaavasti
| S(z) = |
adz+bd
d(cz+d)
|
= |
bcz+bd
d(cz+d)
|
= |
b(cz+d)
d(cz+d)
|
= |
b
d
|
. |
|
Olkoon D = ad-bc ¹ 0. Erotetaan kaksi tapausta:
a) c ¹ 0. Kuvaus
S(z) = [(az+b)/(cz+d)] on
määritelty, kun cz+d ¹ 0
eli kun z ¹
-d/c. Kuvaus on bijektio
| C\ |
ģ
ķ
ī |
- |
d
c
|
ü
ż
ž |
®
C\ |
ģ
ķ
ī |
|
a
c
|
ü
ż
ž |
, |
|
sillä yhtälöllä
on täsmälleen yksi ratkaisu z, kun w ¹ a/c. (Voidaan jo nyt
havaita, että S(-d/c) = „ ja S(„) =
a/c. Kuvaus S on siis bijektio
CČ{ „}
® CČ{
„}).
b) c = 0. Koska ad-bc
¹ 0, on d ¹ 0. Kuvaus
| S(z) = |
az+b
cz+d
|
= |
az+b
d
|
|
|
on nyt määritelty kaikille z Ī
C. Kuvaus on bijektio C®
C, sillä
(koska ad-bc ¹ 0 ja
c = 0, on a ¹ 0). (Tässä
tapauksessa S(„) = „, joten S:CČ{ „} ® CČ{ „} on bijektio.)
4. Määritellään f:C®
C asettamalla
| f ( reij ) = |
r
r+1
|
eij, f(0) = 0. |
|
Koska kuvaus r ®
[(r)/(r+1)] on bijektio ]0,„[ ® ]0,1[ on
bijektio. Jos merkitään z = reij, on r =
|z|. Tällöin
| f(z) = |
1
1+r
|
reij = |
1
1+|z|
|
z. |
|
Kuvaus f(z) = [(z)/(1+|z|)] on siis
bijektio C® U(0,1).
5. Neliöjuuri. Tarkastellaan kuvausta f:z
® z2. Binomiyhtälöllä
z2 = w on kaksi ratkaisua, joille
käytetään merkintöjä Öw ja -Öw. Jos w =
reij, niin
| Öw =
Örei[(j)/2] ja -Öw =
Örei([(j)/2]+p) = -Örei[(j)/2]. |
|
Kuvaus f:C® C on
siis surjektio, mutta ei injektio, sillä pisteille w ¹ 0 kuvautuu aina kaksi pistettä
(On huomattava, että ei ole mitään yleistä tapaa erottaa, kumpi
neliöjuurista on z1 ja kumpi
z2. Jos toista merkitään
Öw:llä, niin toinen on -Öw.)
Olkoon A = {z |
Im z > 0 } ja B = C\{z
| Im z = 0,
Re z ³ 0 }. Silloin
f:A ® B on
bijektio. Sen käänteiskuvausta f-1:B ® A sanotaan neliöjuuren
haaraksi (kuva ), joka on määritelty pitkin positiivista
reaaliakselia aukileikatussa tasossa.
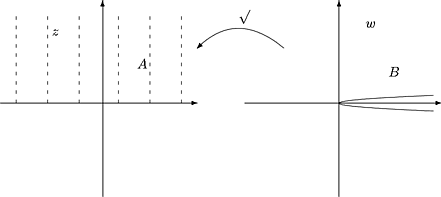Kuva 25: Neliöjuuren haara
Neliöjuuri voidaan määritellä jokaisessa origoon päättyvää
sädettä pitkin aukileikatussa tasossa. Neliöjuuri on
yksikäsitteinen, kun sovitaan, miten taso aukileikataan ja kumpaan
puolitasoon kuuluva haara valitaan. Ennen kuin voidaan ollenkaan
puhua neliöjuuresta, on valittava tason aukileikkaus (kuva ).
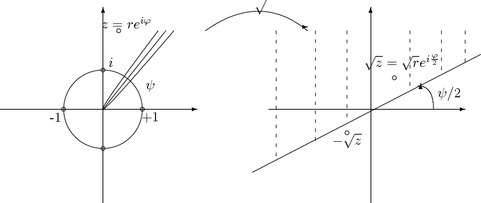Kuva 26: Neliöjuuren määrittely origoon päättyvää sädettä
pitkin
Esimerkki. Mitä vikaa on seuraavassa päättelyssä?
Aukileikataan taso pitkin negatiivista imaginaariakselia (kuva ).
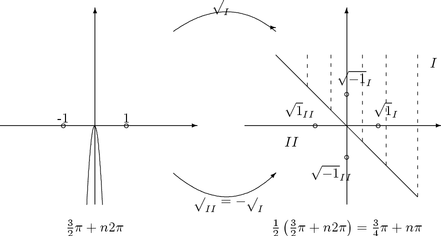Kuva 27: Tason aukileikkaus pitkin negatiivista
imaginaariakselia
Jos Ö määritellään siten, että se
kuvaa aukileikatun tason ylemmälle vinolle puolitasolle I,
niin -Ö kuvaa sen alemmalle puolitasolle
II (kuva 27).
Onko Ö[(-1)] = [(Ö1)/(Ö[(-1)])] ?
Ei ole, sillä Ö[(-1)] = i, Ö1 = 1 ja 1/i =
-i.
Onko sitten -Ö[(-1)] = [(-Ö[(-1)])/(-Ö1)] ?
Ei ole, sillä -Ö[(-1)] = -i ja
-Ö1 = -1 sekä [(-i)/(-1)] =
i ¹ -Ö[(-1)].
Haaralle I on siis
Ö[(-1)]I ¹
[(Ö1I)/(Ö[(-1)]I)] ja haaralle II
on siis Ö[(-1)]II
¹ [(Ö[(-1)]II)/(Ö1II)]. Yhtälöä
ei siis voida johtaa yhtälöstä Ö[(-1)] =
Ö[(-1)], määriteltiinpä neliöjuuri miten
hyvänsä.
Voidaan huomata, että
|
|
__
Ö-1
|
= |
Ö1
|
ja - |
|
__
Ö-1
|
= |
-Ö1
|
, |
|
sillä
Siis
pätee haaralle I, mutta ei haaralle II.
pätee haaralle II, mutta ei haaralle I.
6. Kuutiojuuri. Kuvaus f(z) =
z3 on injektio esimerkiksi alueessa 0 <
argz < [(2p)/3]. Sen kuva on
pitkin positiivista reaaliakselia aukileikattu taso. Kuutiojuurella
on tässä alueessa kolme haaraa, joiden kuvana ovat alueet (kuva )
Yleisesti voidaan määritellä
nÖ{w},
n = 2,3,4,¼.
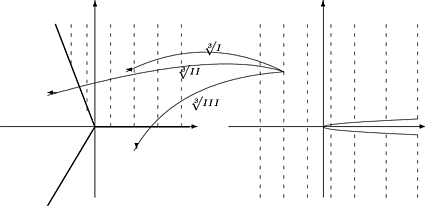Kuva 28: Kuutiojuuren haarojen kuvajoukot
Kuva 29: Suora z+[`(z)]-1 = 2
Esimerkki. Määrää suoran z+[`(z)]-1 = 0 kuva Möbius-kuvauksessa
S(z) = [(z+1)/(z)].
Mikä suora? Yleinen tapa: x-akselin leikkauspisteessä on
z = [`(z)] = x. Siis
2x = 1 eli x = 1/2.
y-akselin leikkauspisteessä on z = iy,
[`(z)] = -iy. Siis
iy-iy-1 = 0 ei toteudu. Kyseessä on siis suora
x = 1/2 (kuva
29).
Kuvan yhtälö:
Ympyrä: z[`(z)]+az+b[`(z)]+g = 0,
a = [`(b)], g < ab
a = b = -2,
g = 3, 3 < (-2)(-2) = 4.
Jos a = a-ib ja b = a+ib, niin keskipiste on
(-a,-b) ja säde
Ö{a2+b2-g}.
Kuvana on siis ympyrä, jonka keskipiste on (2,0) ja säde on 1.
Saamme erikoistapauksen yleisestä tuloksesta: Möbius-kuvaus kuvaa
suoran ympyräksi (tai suoraksi).
Yleisesti suoran x = n yhtälö kompleksimuodossa
on
eli
Vastaavasti suoran y = n yhtälö kompleksimuodossa on
eli
Kertomalla i:llä saadaan yhtälö normaalimuotoon az+b[`(z)]+g = 0,
a = [`(b)] ja g Ī R:
3.2 Kuutiojuuri
reaalifunktiona ja kompleksifunktiona
.
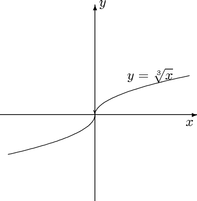Kuva 30: Funktion x ®
x3 kuvaaja
Kuvaus f:x ® 3Ö{x} on
määritelty kaikille x Ī R.
Sen derivaatta
on määritelty kaikille x ¹ 0.
Arvolla x = 0 käyrän tangentti on pystysuora eikä funktiolla
ole äärellistä derivaattaa. Jatkossa nähdään, että jo tämä riittää
osoittamaan, ettei reaalista kuutiojuurta voida luonnollisella
tavalla jatkaa kompleksifunktioksi.
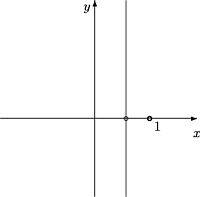
Tarkastellaan kuutiojuurta kompleksifunktiona. Otetaan
määrittelyjoukoksi pitkin negatiivista imaginaariakselia
aukileikattu taso A = C\{ z | Re z = 0, Im z
£ 0 } = C\{ z | argz = [(3p)/2] } (kuva ).
Kuva 31: Kuutiojuuren määrittelyalue
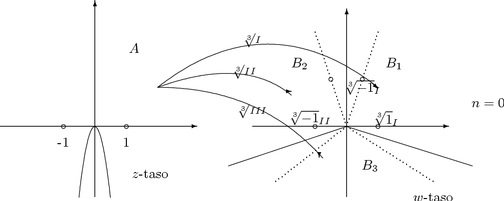
Kuutiojuurella on A:ssa kolme haaraa, joiden maaleina
ovat sektorialueet
|
|
|
|
|
ģ
ķ
ī |
w Ī
C |
ź
ź |
- |
p
6
|
< argw < |
p
2
|
ü
ż
ž |
n = 0 |
|
|
|
|
|
ģ
ķ
ī |
w Ī
C |
ź
ź |
|
p
2
|
< argw < |
7p
6
|
ü
ż
ž |
n = 1 |
|
|
|
|
|
ģ
ķ
ī |
w Ī
C |
ź
ź |
|
7p
6
|
< argw < |
11p
6
|
ü
ż
ž |
n = 2 |
|
|
|
|
Kuutiojuuren haarat ovat:
3Ö{
}I kuvaa positiivisen reaaliakselin
positiiviselle reaaliakselille ja negatiivisen reaaliakselin
suoralle argw = [(p)/3].
3Ö{
}II kuvaa positiivisen reaaliakselin suoralle
argw = [(2p)/3] ja negatiivisen
reaaliakselin negatiiviselle reaaliakselille (argw =
[(3p)/3]).
3Ö{
}III kuvaa positiivisen reaaliakselin suoralle
argw = [(4p)/3] ja negatiivisen
reaaliakselin suoralle argw = [(5p)/3].
Reaalinen kuutiojuuri f saadaan siis ottamalla 3Ö{
}I positiivisella reaaliakselilla ja 3Ö{
}II negatiivisella reaaliakselilla ja
määrittelemällä f(0) = 0.