Näistä tehtävistä odotan kunkin ratkaisevan mitkä tahansa kuusi.

1. Laske

35 æ ç è kpl kk ö ÷ ø · é ê ë 14 æ ç è mk kpl ö ÷ ø + 15 æ ç è min kpl ö ÷ ø · 1 60 æ ç è h min ö ÷ ø ·65 æ ç è mk h ö ÷ ø ù ú û .

2. Määrää seuraavan yhtälön puuttuvat mittayksiköt niin, että yhtälö on dimensiohomogeeninen:

280 000 (?) ·4,5 æ ç è % vuosi ö ÷ ø =  é ê ë x æ ç è mk kk ö ÷ ø - 420  æ ç è mk kk ö ÷ ø ù ú û ·12 (?) ·0,72 (?).

3. Ratkaise yhtälöt

a)  2x-1 3 =  5x+4 6 b)  3+5x 2 - 2-4x 5 =  3x 4 .

4. Ratkaise epäyhtälöt

a)  2-5( x-3) < 4x+7  b)  x 3 - x+2 6 >  x 2 .

5. Määritä suoran yhtälö ja piirrä suora, joka

a) kulkee pisteen (0,1) kautta ja jonka kulmakerroin on -[2/3],
b) kulkee pisteiden (-1,2) ja (2,-1) kautta.
 
6. Ratkaise yhtälöpari ja piirrä suorat

ì í î y =  2x-1  y =  -x+3

Kaksi tehtävää kääntöpuolella!

7. Erään funktion y = f(t) kuvaaja näyttää välillä [-20,20] seuraavalta:
ja on syytä olettaa, ettei sen käytöksessä muualla ole mitään yllättävää.
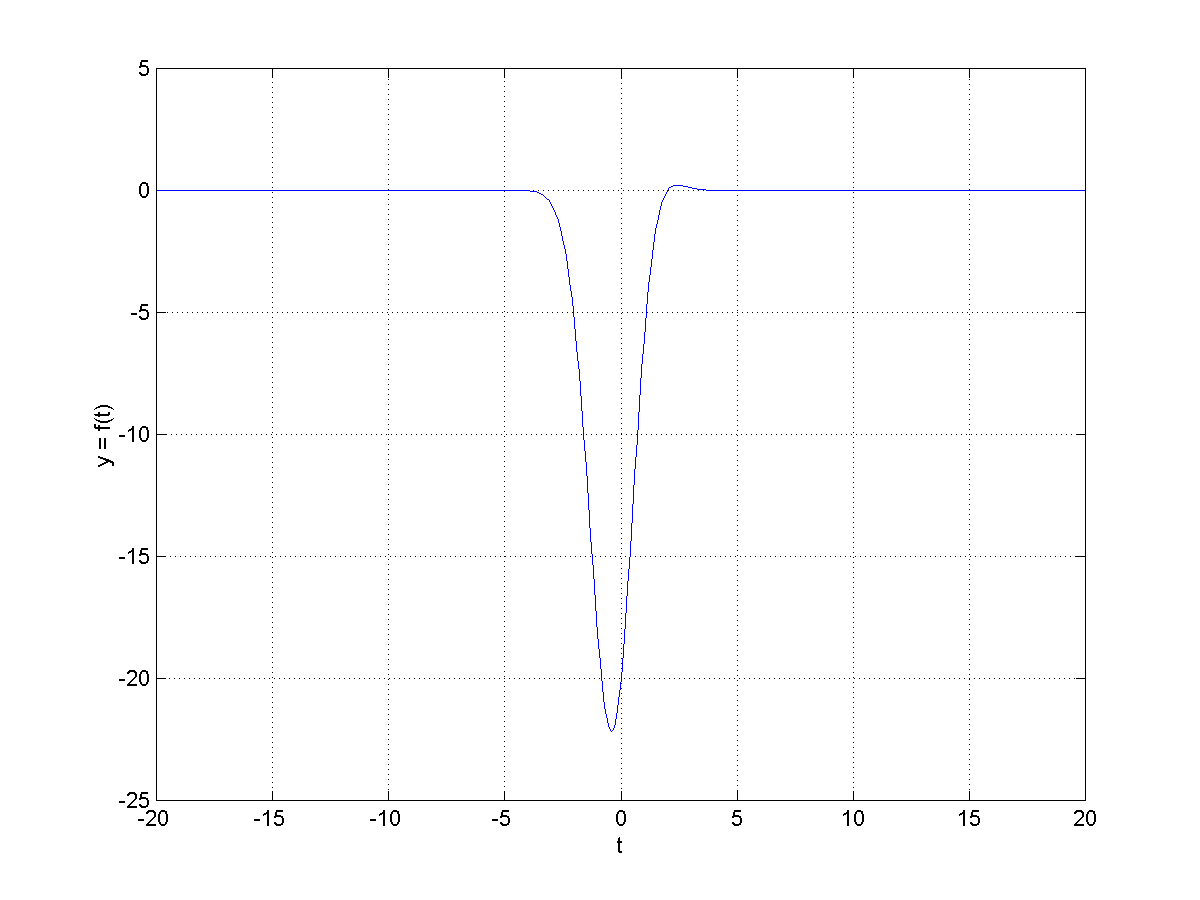
a) Valitse funktiolle sopiva lähtö- eli määrittelyjoukko ja maalijoukko.
b) Määritä vastaava arvojoukko.
c) Selvitä millä väleillä funktio on nouseva eli kasvava, ja millä väleillä laskeva eli vähenevä.
 
8. Piirrä reaalifunktion f(x) = -3x² + x kuvaaja xy-koordinaatistoon välillä -1 £ x £ 1, ja määritä kuviosi perusteella funktion f nollakohdat sekä suurin arvo kyseisellä välillä.