graphicx

Matematiikan yleisopintojakso 2000

Kotilaskujen ohjausta viikoilla 38-49 salissa M9 ajankohtina ma 14-18, ti 14-18 ja ke 14-16.

Tätä jaettiin paperilla 37. viikolla 2000

Joukko-oppia

Käsite joukko on matematiikan keskeisimpiä apuvälineitä. Sitä ei tässä määritellä sen tarkemmin kuin:

Matemaattisena käsitteenä joukko on kokonaisuus, jossa voi olla jäseninä, alkioina, lukuja, symboleja, esineitä tai muita olioita, vaikkapa muita joukkoja. Rajatapauksena joukoksi hyväksytään myös tyhjä joukkoÆ = { }, jossa ei ole yhtään alkiota.
Mille tahansa joukolle A ja jokaiselle oliolle x pitää olla voimassa jompikumpi seuraavista
1) x on joukon A alkio (merkitään x ÎA), tai
2) x ei ole joukon A alkio (merkitään xÏA).

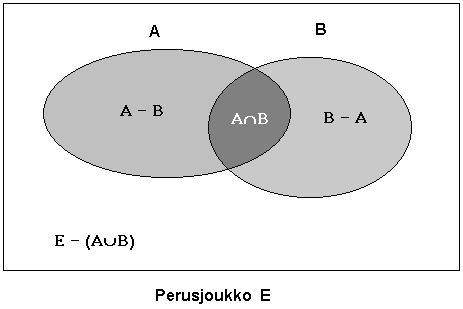
Huomautus. Joukko ei saa olla itsensä alkiona. Pidättäydymme myös puhumasta kaikkien joukkojen joukosta!

Joukkoja käsiteltäessä - erityisesti joukon ulkopuolelle jäävien alkioiden tarkastelussa - on kätevää ottaa käyttöön sopiva, kaikki tarkasteltavat alkiot sisältävä joukko, perusjoukko, jonka suhteen tarkastelu tapahtuu.

Joukko-opin perusoperaatiot ovat

yhdiste: AÈB on joukko, jonka alkioina ovat kaikki joukkojen A ja B alkiot
leikkaus: AÇB on joukko, jonka alkioina ovat kaikki molempiin joukkoihin A ja B kuuluvat alkiot
erotus: A \ B = A -B on joukko, jonka alkioina ovat kaikki ne joukon A alkiot, jotka eivät ole joukossa B
komplementti: A` = E \ A on joukko, jonka alkioina ovat kaikki ne perusjoukon alkiot, jotka eivät kuulu joukkoon A

Joukkojen suhteita havainnollistetaan usein nk. Venn-diagrammeilla:

Joukko-opillisia vertailuja ovat

kuulua joukkoon: x ÎA, x kuuluu joukkoon A (vastaavasti ei kuulu: xÏA)
olla osajoukko: A Ì B tai A Í B, jokainen joukon A alkio on myös B:ssä
samuus: A = B, joukoissa on samat alkiot (vastaavasti eri joukot: A ¹ B)

Esimerkki 1. Olkoon E = {1,2,3,4,5,6,7,8,9,10} ja A = {2,4,6,8,10}, B = {1,3,6,9}, C = {4,8}. Silloin E kelpaa perusjoukoksi, ja esimerkiksi
B\A = {1,3,9} ja B` = {2,4,5,7,8,10}.

Tehtävä 1. Mikä joukko kelpaisi perusjoukoksi tarkasteltaessa edellisten joukkojen A, B ja C lisäksi joukkoa D = {1,5,{4,8}}?

Tehtävä 2. Tarkastellaan vielä yo. joukkoja A, B, C ja D. Mitkä seuraavista ilmauksista ovat järjellisiä, ja mitkä niistä ovat tosia:

a)	3 Î C	f)	C Í A
b)	3 Î CÈB	g)	A ÈB = E
c)	4 Ï B	h)	D Í E
d)	{3,6} Í B	i)	C Î D
e)	3 Í B	j)	E\A = {1,2,3,4,5}

Tehtävä 3. Olkoot A,B,C,DÍE. Esitä Venn-diagrammina joukot

a) [`(A)]Ç[`(B)]Ç[`(C)]Ç[`(D)]	b) (AÇD)\C
c) (DÇC)È(BÇC)\A	d) [`(AÈBÈCÈD)]

Ratkaisu. Vasen a) ja d), keskellä b), oikealla c).

Tehtävä 4. Mitä joukkoa esittää seuraavan Venn-diagrammin harmaa alue?

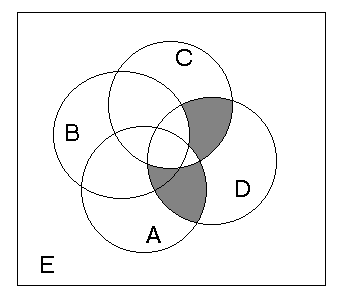
Vastaus. ((AÇD)\C)È((CÇD)\(AÈB))

Footnotes:

File translated from T_EX by T_TH, version 2.64.
On 14 Sep 2000, 16:09.