Algebra, syksy 1999

Kotitehtävät 12-13 (tehtävät 4,5,6,9 ja 18-19 palautettava ma 13.12.1999 klo 12 mennessä)


Ilmoituksia loppuajan ohjelmasta:
Viimeinen varsinainen luokkatunti 7.12.1999, jolloin 4. pistokkaat. Palautan kotitehtävät 11 ilmeisesti vasta tiistaina, jolloin saatte ratkaisut.
Jokainen kurssilainen joutuu antamaan palautetta Web-lomakkeen kautta; lomake ei ole vielä valmis, mutta ilmoitan sähköpostitse osoitteen sitten kun on.
Matkan takia ei ole algebran opetusta 8.-10.12.1999.
Kertaus- ja palautetilaisuus tiistaina 14.12.1999 klo 14-16 M2 (huom! aika ja paikka).
2. välikoe (yksilötentti) perjantaina 17.12.1999 klo 8-10 M1.

1. Olkoon G : = Z6×Z2 ja määritellään laskutoimitus + joukossa Z6×Z2 seuraavasti:
(a,b)+(c,d) : = (a +6 c, b +2 d).
Silloin (G,+) on ryhmä. Olkoon N syklinen aliryhmä á(1,1)ñ. Etsi tekijäryhmä G/N. Minkä tutun ryhmän kanssa tekijäryhmä G/N on isomorfinen?

2. Olkoon a Î G jokin ryhmän G alkio. Todista, että kuvaus f: G ® G, f(x) : = axa-1, on isomorfismi.

3. Todista, että funktio f kompleksilukujen kertolaskuryhmältä (C\{0},*) reaalilukujen kertolaskuryhmälle (R\{0},·), jolle f(x+yi) : = Ö{x2+y2}, on homomorfismi. Toisin sanoen f kuvaa kompleksiluvun sen modulille eli itseisarvolle. Mikä on homomorfismin f ydin?

4. Olkoot G, G¢ ja G¢¢ ryhmiä ja funktiot f:G ® G¢ sekä g: G¢® G¢¢ homomorfismeja. Osoita, että näiden yhdistetty kuvaus G ® G¢¢ on homomorfismi. Mitä voidaan sanoa funktion f ja yhdistetyn funktion ytimistä suhteessa toisiinsa?

5. Osoita, että isomorfismin käänteiskuvaus on olemassa ja on isomorfismi.

6. Todista Lause 11.4: Olkoon (R,+,·) rengas ja 0R sen neutraalialkio. Silloin kaikilla a Î R on 0R·a = 0R ja a·0R = 0R.

7. Todista, että renkaassa R on voimassa

a(b-c) 
= 
ab-ac
(a-b)c
= 
ac-bc
kaikille a,b,c Î R (siis Lemman 11.5 kohdat 4 ja 5).

8. Olkoon (R,+,·) vaihdannainen ykkösellinen rengas. Todista, että jos tulon supistussäännöt

ax = ay
 Þ
x = y
xa = ya
 Þ
x = y
ovat voimassa kaikilla x,y Î R ja a Î R\{0R}, niin (R,+,·) on kokonaisalue (Lauseen 11.9 todistuksen toinen suunta).

9. Määritellään joukossa Z uusi yhteenlasku Å ja uusi kertolasku \odot seuraavasti:

aÅb
: = 
a + b - 1,
a\odot b
: = 
a + b - ab.
Osoita, että (Z,Å,\odot) on kokonaisalue.

10. Todista, että joukko Z [i] : = { a+bi   |  a,b Î Z } on kokonaisalue, kun laskutoimituksina ovat tavallinen kompleksilukujen yhteenlasku ja kertolasku. Tätä joukkoa kutsutaan Gaussin kokonaisluvuiksi.

11. Renkaan alkiota x sanotaan idempotentiksi, jos x2 = x.
       a) Etsi kaikki renkaan Z12 idempotentit alkiot.
       b) Onko kaikissa renkaissa idempotentteja alkioita?
       c) Miten renkaan R idempotentit alkiot ja kokonaisalueen käsite liittyvät toisiinsa?

12. Olkoon (F,+,·) kunta. Todista, että tällöin (F\{0F},·) on Abelin ryhmä (Lause 11.13).

13. Olkoon Z[Ö7] : = { a + bÖ7  | a,b Î Z  }. Osoita, että Z[Ö7] on renkaan R alirengas.

14. Olkoon R rengas, ja olkoon U(R) niiden renkaan R alkioiden joukko, joille on olemassa käänteisalkio renkaan kertolaskun · suhteen.
a) Mitä ovat U(Z), U(Z12) ja U(Z7)?
b) Todista, että (U(R),·) on ryhmä.

15. Olkoon R kokonaisalue. Todista, että joukko

T : =  ì
í
î		 æ
ç
è
a
a
0 
0
ö
÷
ø		 ê
ê
ê		 a Î R ü
ý
þ
on matriisirenkaan M(R) alirengas. Onko se kokonaisalue? Entä kunta?

16. Ratkaise yhtälöpari 2x + 3y = 2 ja 4x - 3y = -3 kunnassa (Z11,+11,*11).

17. Sijoittele seuraavat renkaat oikeaan lokeroonsa alla olevassa kuviossa:

R, Z, C, Z16, Z17, 5Z, M(R), M(Z2), ({0,4,8,12,16},+20,*20), T1, T2, missä

T1 : =  ì
í
î		 æ
ç
è
a
a
0 
0
ö
÷
ø		 ê
ê
ê		 a Î Z3 ü
ý
þ		     ja   T2 : =  ì
í
î		 æ
ç
è
a
0
0 
b
ö
÷
ø		 ê
ê
ê		 a,b Î Z3 ü
ý
þ		 .

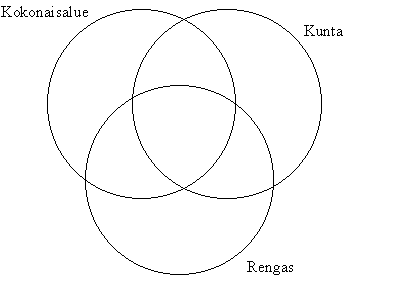
Perustele, miksi sijoitit matriisirenkaat T1 ja T2 sinne minne sen sijoitit.
Perustele, miksi sijoitit renkaan ({0,4,8,12,16},+20,*20) minne sijoitit.
Miksi jotkut alueet jäävät tyhjiksi?

18-19. ISETL-demojen 13 tehtävät 6,7,8 (paperitulosteena).

20. Täytät ja palautat (sähköisesti) Web-palautelomakkeen 20.12.1999 mennessä.

File translated from TEX by TTH, version 1.96.
On 2 Dec 1999, 14:13.