Ratkaisu
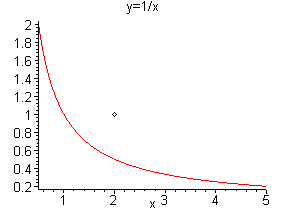
Pisteen (2,1) etäisyyden neliö käyrästä y=1/x on muotoa
|
|
| | |
(2-x)2+(1-y)2 = (2-x)2+(1-1/x)2 |
|
| | |
|
|
|
Pisteen (2,1) ja käyrän y=1/x lyhin etäisyys löydetään
derivaatan D¢(x) nollakohdista.
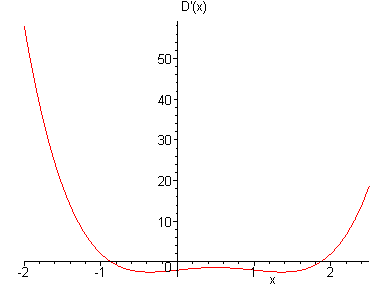
Derivaattafunktion kuvaajasta nähdään, että välttämättä etäisyysfunktion D
minimoiva nollakohta on välillä (1,2). Valitaan siis alkuarvaukseksi x0=2
ja iteroidaan ratkaisuja Newtonin kaavan mukaan
|
|
| | |
| | |
xn- |
2xn4-4xn3+2xn-2
8xn3-12xn2+2
|
. |
|
|
|
|
Saadaan
| xn | D¢(xn) |
| 2.0000 | 2.0000 |
| 1.8888 | 0.2801 |
| 1.8675 | 0.0091 |
| 1.8667 | 0.0000 |
| 1.8667 | |
3. iteraatio antaa ratkaisun x=1.8667 neljän desimaalin tarkkuudella. (Tarkka
ratkaisu 1/2+1/2Ö{3+2Ö5} » 1.866760399.)



