Dynamic Geometry Software Sebastian Lisken
lisken@Mathematik.Uni-Bielefeld.DE

Abbreviations: GSP = The Geometer's Sketchpad


The concept of dynamic geometry software

 
• Nick Jackiw (GSP developer): Dynamic Geometry is about exploring geometry in a lab, finding and testing your own conjectures.
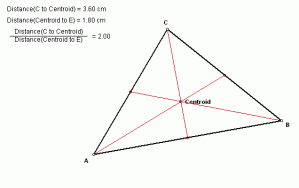
• Example: See how one of the triangle's many properties can be explored using GSP.
• Constructions are created in terms of base objects (mostly free points) and derived objects (lines, segments, circles, intersection points, points restricted to lines and circles, and many more). The geometrical relations between objects are determined in this way. Dragging the base objects is possible, derived objects are recalculated to keep the relations true.


First experience

• Exercise 1: How could the midpoint of a segment be constructed?
• Exercise 2: Construct a sketch that illustrates a simple geometrical conjecture, then see if you can find the proof with the help of Sketchpad's capabilities.
• Exercise 3: Remember the classical definition of a parabola? Could Sketchpad construct a parabola in this way?


Where do we go from here

Using some of its more sophisticated capabilities, you can make Sketchpad a great tool to illustrate and demonstrate almost all kinds of mathematics.
 

A simple but nice example suitable for a school lesson.
 

The power of buttons, and some triangle terminology. More about triangles. (The second link is a great source for terminology, too)
 

Using measurements, calculations and a coordinate system, all kinds of function graphs can be created.
 

You can even make constructions appear on Web pages themselves, without the need for GSP as an external viewer. This is possible through the use of a Java applet, JavaSketchpad (JSP), which is related to GSP. JSP constructions can be created out of GSP files, but not all features are supported. Drag A, B and C:		 Sorry, this demo requires a Java-compatible web browser.
The original html product created with GSP ...

Sebastian Lisken, Oct 11, 1999