A few questions before we
start:
Sketchpad in brief
Some basic guidelines and remarks
about using The Geometer's Sketchpad.
-
Sketchpad has just a few tools
to create very simple objects: points, circles, segments/rays/lines, and
labels/text fields. Everything else is created through the "Construct",
"Transform", "Measure", and "Graph" menus.
See the Quick Reference
card for an overview of all the constructions Sketchpad can perform.
-
The constructions in the menus
all create derived objects (i.e. objects that depend on other ones).
Sketchpad strictly follows a standard Windows/Mac interface philosophy:
In order to anything with an object (like constructing a new object out
of it), you first select the existing object(s) and
then perform
actions on these objects to achieve what you want. For selecting, there
is a whole range of functions available using the mouse, the Shift key
and the Edit menu (and more).
This
philosophy
can make Sketchpad seem somewhat secretive about what it has to offer.
You can have a hard time
selecting the right objects for the construction you want.
Solution: If the desired menu item is grey, move down
to it and press F1 for help. Or look at the Quick Reference.
On
the
other hand, if you know what you're doing and learn to use certain tricks
(e.g. keyboard shortcuts, ways of constructing several things at once)
you can be very efficient in working with Sketchpad, significantly faster
than with other Dynamic Geometry programs.
-
For transformations,
before selecting the objects to be transformed, you must also give Sketchpad
the parameters for the desired transformation (by "marking" a center
for rotations and dilations, a scaling factor for dilations, a vector
for translations, a mirror for reflections). This can make transformations
slightly difficult to use. More confusingly, sometimes it is possible to
choose the transformation from the menu and then click on the things you
forgot to mark before (transformation vectors, measured scale factors or
angles).
-
You can construct measurements
of several things within your sketch. One specific "measurement" is the
calculation,
which can take values from other measurements. There are several ways of
constructing objects out of measurements, too, you can thus "put back"
numeric results into geometry -- this feature, especially with the Graph|Plot
and Locus constructions, makes all kinds of mathematics representable.
-
Sketchpad is especially valuable
for didactics and presentations because of its variety of buttons.
Buttons can show and hide extra objects, drag your sketch into some predefined
configuration, animate for automatic movement or "play" other buttons in
sequence (pauses for dramatic effect are possible).
-
Scripts are a very powerful
way of shortening your work and indeed extending the set of constructions
available in Sketchpad. You can record your constructions while
you create them, later you play back the script to repeat your actions
on other objects.
-
The Correction functions in
Sketchpad could be richer. You can Undo every step of your construction,
but what if you then want to "Redo" them on a slightly different set of
starting objects? Scripts can sometimes provide a solution. You can make
a script out of something previously constructed which will hopefully
reflect the actions you will have to "redo" (but not always with the result
you want).
Let's dive in
Remember what the problem was
in constructing a parabola? Often you want to create object that has certain
properties (e.g. a point that has the same distance to a given point and
a given line, or the same distance to two given points). But you can't
tell Sketchpad to find that object for you, it's you who must find
a way to ensure that those properties hold -- that's what geometric construction
is about.
Classical (Euclidian)
constructions
Objective: to get familiar
with the tools and items in the "Construct" menu, possibly have some first
experience with measurements and scripts.
Can you find out ways (using
all Sketchpad functions you want) to construct:
-
specific quadrilaterals: a trapeze,
a parallelogram and a square;
-
specific triangles: a right,
an isosceles, an equilateral triangle;
-
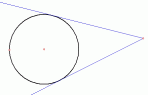
(for a special beginner's award
from Lauri:) the tangents from a point to a circle (the point of course
being outside the circle)?
Who can come up with the most
exotic constructions?
There is always more than one way, and each has its own advantages.
And let's not forget, Geometry has close links with arts and creativity.
If you want, you can include
measurements to confirm numerically that your constructions are correct.
You could also make scripts out of some of your constructions and save
them for later use.
In fact, this is a very good opportunity to learn about the "Make Script" function
so that you don't have to repeat these basic constructions later on in your
"Sketchpad career".
Sebastian Lisken,
Oct 11, 1999