Example from the HTML document

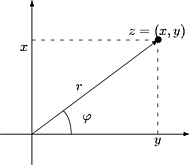
Kertolaskun laajentaminen ei ole yhtä helppoa, sillä valmiina ei ole sopivaa "vektorituloa". Kertolaskun laajentamista varten esitetään tason pisteet z = (x,y) ¹ (0,0) napakoordinaattien r ja j avulla:

ì
í
î
x = r cosj
y = r sinj

Kuva 1: Kompleksilukujen napakoordinaattiesitys

Merkitään z = (r,j). Tulo on nyt määriteltävissä yksinkertaisella kaavalla

z1z2 = (r1r2,j1 + j2).

Siis: Pisteiden z1 ja z2 etäisyydet origosta kerrotaan keskenään sekä vaihekulmat lasketaan yhteen. Erikoisesti on z1z2 = 0 aina ja vain kun z1 = 0 tai z2 = 0.

Tarkastellaan reaalilukujen kertolaskua tämän uuden kertolaskun valossa. Olkoon z = (r,j) reaaliluku. Tällöin aina |z| = r. Lisäksi

z = r > 0
Û
j = 0 + n2p
z = -r < 0
Û
j = p+ n2p
Jos nyt z1 = (r1,j1) ja z2 = (r2,j2) ovat kaksi reaalilukua, niin z1z2 = (r1r2,j1+j2), joten
z1z2 > 0
Û
j1+j2 = 0+n2p
Û
j1 = j2 = 0+n2p    tai     j1 = j2 = p+n2p
Û
z1 > 0     ja     z2 > 0     tai     z1 < 0     ja     z2 < 0.

File translated from TEX by TTH, version 2.32.
On 29 Jul 1999, 10:12.