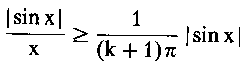
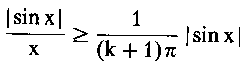
gilt, erhält man
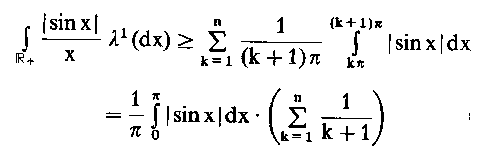
III. Berechnung des Integrals G. -- Die vorausgehenden Betrachtungen lehren, daß Integrale, die dem Leser u.U. nur als Riemann-Integrale bekannt sind, unter den genannten Voraussetzungen sofort als Lebesgue-Integrale interpretiert werden können. Bekannte Formeln und Rechenregeln für Riemann-Integrale stehen uns daher auch in der Lebesgueschen Theoric zur Verfügung. Zur Illustration betrachten wir die auf IR+ X IR definierte nichtnegative Funktion

Sie ist insbesondere für festes x in IR, als Funktion von ![]() auf IR stetig und damit über jedes kompakte Intervall in IR
auf IR stetig und damit über jedes kompakte Intervall in IR ![]() -integrierbar.
Wegen
-integrierbar.
Wegen ![]() gilt
gilt
