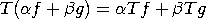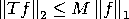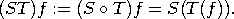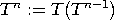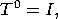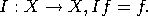= 0 &arrowdblboth; f = 0
= 0 &arrowdblboth; f = 0
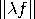 =
= 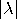

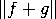 ≤
≤  +
+ 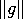
 : X &multiply; X → R+ on avaruuden X normi, mikäli se täyttää
ehdot
: X &multiply; X → R+ on avaruuden X normi, mikäli se täyttää
ehdot
 = 0 &arrowdblboth; f = 0
= 0 &arrowdblboth; f = 0
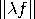 =
= 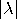

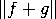 ≤
≤  +
+ 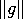
kaikilla f, g &element; X, λ &element; F. Vektoriavaruutta, jossa on määritelty normi kutsutaan
normiavaruudeksi.
Määritelmä 2 Normiavaruuden X pisteiden jono &braceleft;fn &braceright; suppenee kohti
pistettä f, mikäli kaikilla ϵ > 0 on olemassa N &element; N siten, että 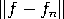 < ϵ
kaikilla n ≥ N. Suppenemistapauksessa kirjoitamme f = lim n→∞ fn .
Määritelmä 3 Jono &braceleft;fn &braceright; &reflexsubset; X on Cauchy`n jono, mikäli jokaista ϵ > 0
vastaa N &element; N siten, että
< ϵ
kaikilla n ≥ N. Suppenemistapauksessa kirjoitamme f = lim n→∞ fn .
Määritelmä 3 Jono &braceleft;fn &braceright; &reflexsubset; X on Cauchy`n jono, mikäli jokaista ϵ > 0
vastaa N &element; N siten, että 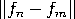 < ϵ kaikilla n, m ≥ N
Määritelmä 4 Sanomme, että normiavaruuden X pisteiden &braceleft;fn &braceright;
muodostama sarja &summationtext;
n = 1∞fn suppenee, jos sen osasummien
< ϵ kaikilla n, m ≥ N
Määritelmä 4 Sanomme, että normiavaruuden X pisteiden &braceleft;fn &braceright;
muodostama sarja &summationtext;
n = 1∞fn suppenee, jos sen osasummien
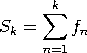
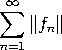
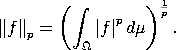
Seuraavan lauseen avulla saadaan eräs kriteeri sille, milloin jokin normiavaruus on täydellinen. Lause 1 Normiavaruus X on täydellinen jos ja vain jos jokainen itseisesti suppeneva sarja suppenee. Määritelmä 6 Olkoon X1 ja X2 vektoriavaruuksia. Tällöin kuvaus T : X1 → X2 on lineaarinen, mikäli