Jaollisuus

Tässä luvussa liikutaan lähinnä kokonaislukujen joukossa

Tämä aksiooma kuulostaa intuitiivisesti selvältä. Se ei kuitenkaan ole voimassa esimerkiksi rationaaliluvuille: esimerkiksi joukossa } ei ole pienintä alkiota.

Ala-asteella tehdään paljon jakolaskuja. Esimerkiksi tai jakolaskun tuloksena on 145 ja jakojäännöksenä 14. Äskeinen lasku voidaan ilmoittaa myös muodossa

Tämä idea voidaan ilmoittaa myös muodollisesti:

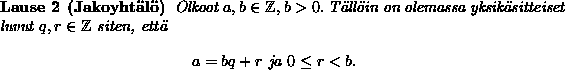
.Olkoot b>0. Tarkastellaan kaikkia muotoa a-bx olevia kokonaislukuja, missä x on kokonaisluku. Osoitetaan ensin, että jotkin näistä kokonaisluvuista ovat ei-negatiivisia.

1. Jos niin silloin on ei-negatiivinen. Siis a-bx on ei-negatiivinen, kun x=0.

2. Jos a<0, niin silloin on ei-negatiivinen, koska sekä a ja 1-b ovat negatiivisia. Siis a-bx on ei-negatiivinen luvulle x=a.

Siten joukko ja on epätyhjä.

Aksiooman mukaan joukossa S on pienin alkio. Olkoon r tämä pienin alkio. Koska niin r on muotoa r=a-bx jollekin ja merkitään x=q. Siis

Koska niin Todistetaan nyt, että r<b. Oletetaan, että Silloin joten

Koska a-b(q+1) on ei-negatiivinen, se kuuluu joukkoon S. Mutta koska b on positiivinen, r-b>r. Siispä

mikä osoittaisi, että a-b(q+1) olisi pienempi kuin r. Mutta r on joukon S pienin alkio, ja näin on saatu ristiriita. Siispä on oltava r<b.

Lopuksi meidän täytyy osoittaa, että q ja r ovat ainoat tällaiset luvut (eli joille a=bq+r), eli että q ja r ovat yksikäsitteisiä. Tämän todistamiseksi oletetaan, että olisi olemassa toiset luvut ja joille myös pätisi

Joko tai Oletetaan, että Vähentämällä kaksi yhtälöä toisistaan saamme

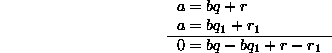
Viimeisen yhtälön mukaan on luvun b monikerta. Mutta b>0 ja joten on välttämättä ei-negatiivinen kokonaisluku. Siispä on jokin luvuista 0b,1b,2b,3b,4b,... .Mutta joten Näin ollen ainoa mahdollisuus on, että Siten Lopuksi, koska ja b>0, on myös eli

Samanlainen päättely todistaa yksikäsitteisyyden myös siinä tapauksessa, kun

\