=1000 =16truecm =25truecm truemm truemm
=0pt
Analyysi 1, 1998, Harjoitus 11
Teht„vi„:
1. Olkoon 
jatkuva funktio siten, ett„
f(0)=2 ja 
ja
f on v„henev„, kun 
. Osoita, ett„ f:ll„ on suurin arvo
:ss„.
2. Osoita, ett„ funktiolla f,
on suurin ja pienin arvo :ss„.
3. Oletetaan, ett„ f(0)=0 ja 
.
Todista, ett„ on olemassa 
siten, ett„
, kun 
.
Kotiteht„v„t:
1. Olkoon funktio f jatkuva ja
.
a) N„yt„ esimerkki tapauksesta, jossa funktiolla
f on suurin arvo, mutta ei pienint„ arvoa.
b) N„yt„ esimerkki tapauksesta, jossa funktiolla
f on pienin arvo, mutta ei suurinta arvoa.
c) N„yt„ esimerkki tapauksesta, jossa funktiolla
f on sek„ suurin ett„ pienin arvo.
d) Osoita: Jos f(0)=0, niin funktiolla f
on :ss„ pienin arvo.
2. Olkoon jatkuva funktio siten, ett„
f(1)=-1 ja |f(x)-1|<1, kun 
. Osoita, ett„ f:ll„ on :ss„
pienin arvo.
3. Osoita, ett„ funktiolla f
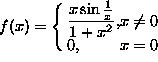on :ss„ suurin arvo.
Tee teht„v„t 4, 5 ja 6 derivaatan m„„ritelm„n nojalla:
4. M„„r„„
a) f'(2), kun 
,
b) g'(x), kun 
.
5. M„„r„„, jos mahdollista, vakio a siten, ett„ funktio
f, 
on derivoituva origossa?
6. Oletetaan, ett„ funktio toteuttaa
ehdon 
kaikilla 
. Osoita, ett„ funktio
g, 
on derivoituva pisteess„ -1, ja m„„rit„ g'(-1).
5. Montako reaalista ratkaisua on yht„l”ll„
?
3. Selvit„ itsellesi k„sitteet: 
ja
.
Olkoon funktio f jatkuva. Oletetaan lis„ksi, ett„ f
on derivoituva, kun 
.
a) Osoita:
on olemassa 
.
b) Osoita: on olemassa
.
Vihje: K„yt„ a)-kohdassa v„liarvolausetta ja b)-kohdassa
esimerkkin„ funktiota f,
4. Montako reaalista ratkaisua on yht„l”ll„ 
?
5. M„„r„„ v„lit, joilla funktio f, 
on
monotoninen. Kun rajoitutaan t„llaiseen v„liin, on funktiolla f
k„„nteisfunktio. Laske n„ille k„„nteisfunktioille 
.
Tulkitse teht„v„ my”s piirt„m„ll„ kuvaajat.
2. K„„nt”puolella on derivaattafunktioiden kuvaajia ja vastaavien funktioiden kuvaajia. Etsi mahdollisimman hyvin toisiinsa sopivat parit.
3. Hahmottele funktion kuvaajaa vastaava derivaattafunktion kuvaaja. (kalvo)