Eulerin ketju on ketju, joka kulkee verkon kaikkien solmujen ja kaarien kautta siten, että jokainen kaari esiintyy ketjussa tasan kerran. Jos verkossa on suljettu Eulerin ketju, on kysessä Eulerin verkko. Yksinkertaistetusti kyseessä on Eulerin verkko, jos verkko voidaan kulkea läpi lähtösolmuun palaten, siten että jokaisessa solmussa on käyty ainakin kerran ja kukin väli on kuljettu täsmälleen kerran.
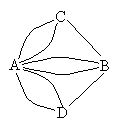
Königsbergin sillat verkko on kuuluisa esimerkki verkosta, joka ei ole Eulerin verkko. Jo Euler selvitti Eulerin ketjun olemassaololle suuntaamattomasta verkosta helposti tarkastettavat ehdot.
Ehdot Eulerin ketjun olemassaololle suuntaamattomassa verkossa: Olkoon G äärellinen, suuntaamaton verkko, jossa ei ole erillisiä solmuja.
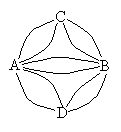
a) Verkossa G on suljettu Eulerin ketju jos ja vain jos G on yhtenäinen ja siinä ei ole paritonasteisia solmuja. Eulerin verkon jokainen Eulerin ketju on suljettu.
b) Verkossa G on avoin Eulerin ketju jos ja vain jos G on yhtenäinen ja siinä on täsmälleen kaksi paritonasteista solmua. Jos verkossa G on yksikin avoin Eulerin ketju, sen jokainen Eulerin ketju on avoin päinään kyseiset paritonasteiset solmut.
Königsbergin sillat-ongelmaa vastaavassa verkossa ei siis voi olla Euletin ketjua, koska kaikki solmuta ovat paritonasteisia. Jos verkkoon lisättäisiin toinen kaari solmujen A ja B välille (ts. rakennettaisiin toinen silta saarien A j B välille) olisi verkossa kaksi parintonasteista solmua (C ja D) sekä kaksi parillisasteista solmua (A ja B).

Ehdot Eulerin ketjun olemassaololle suunnatussa verkossa: Olkoon G äärellinen suunnattu verkko, jossa ei ole erillisiä solmuja. Tällöin verkossa G on Eulerin polku jos ja vain jos G on yhtenäinen ja jompikumpi seuraavista ehdoista on täytetty:
1) Jokaisessa solmussa solmun lähtöaste (siihen osoittavien nuolien lukumäärä) on sama kuin solmun maaliaste (siitä lähtevien solmujen lukumäärä).Kohdan 1) tapauksessa jokainen Eulerin polku on suljettu ja kohdan 2) tapauksessa jokainen Eulerin polku on avoin polku solmusta v solmuun w.2) on olemassa sellaiset solmut v ja w, että v:n lähtöaste = 1 + v:n maaliaste, w:n maaliaste = 1 + w:n lähtöaste ja kaikkien muiden verkon solmujen lähtöaste = maaliaste.
Algoritmi Eulerin ketjun löytämiseksi: Oletetaan, että G on äärellinen suuntaamaton verkko, joka on yhtenäinen ja jonka solmujen asteet ovat parillisia.
Valitaan jokin verkon G solmu v.
Poistetaan jokin siihen liittyvä kaari.
Jos jäljelle jäävä aliverkko on yhtenäinen, otetaan kaari ketjuun, muutoin kaari palautetaan verkkoon ja valitaan uusi.
Siirrytään valitun kaaren toiseen päähän. Menetellään kuten solmun v tapauksessa.
Kun jonkin solmun aste putoaa nollaksi, solmu poistetaan.
Verkossa kuljetaan näin, kunnes kaikki kaaret on poistettu. Poistettujen kaarien muodostama kaarijono on eräs suljettu Eulerin ketju alkuperäisessä verkossa G.
Esimerkki 8 Eulerin ketjun etsiminen verkosta
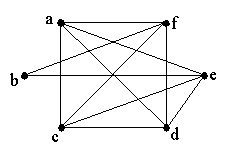
Harjoitustehtävä 7 Ovatko verkot 5 - 7 Eulerin verkkoja? Jos verkko on Eulerin verkko, etsi Eulerin ketju, jos ei perustele miksi ei. Verkkoon 5 voit käyttää apuna seuraavaa: Kokeile
 |
 |
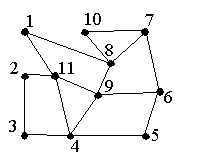 |
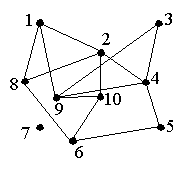
Harjoitustehtävä 8 Vastaa perustellen, ovatko verkot 8 ja 9 Eulerin verkkoja?
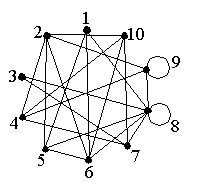 |
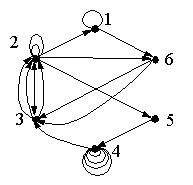 |
Harjoitustehtävä 9 Etsi Eulerin polku Verkosta 9.