Response Analysis


  [Home] [1 Intro] [2 Resp.-Anal.] [3 JavaScript] [4 JS Interf.] [5 Design] [6 Special] [7 Java-Interf.] [Reference] 

Content:

 

Introduction

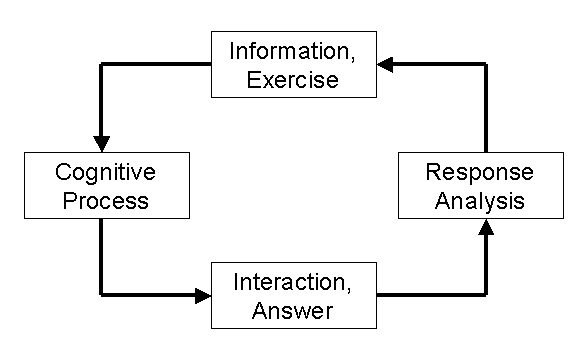
The Cycle of Learning Module:

 

Geometria-examples with Response Analysis

 

Discrete Math Examples (Joensuu):

 

 

 

 

Defining a response analysis with GeoScript

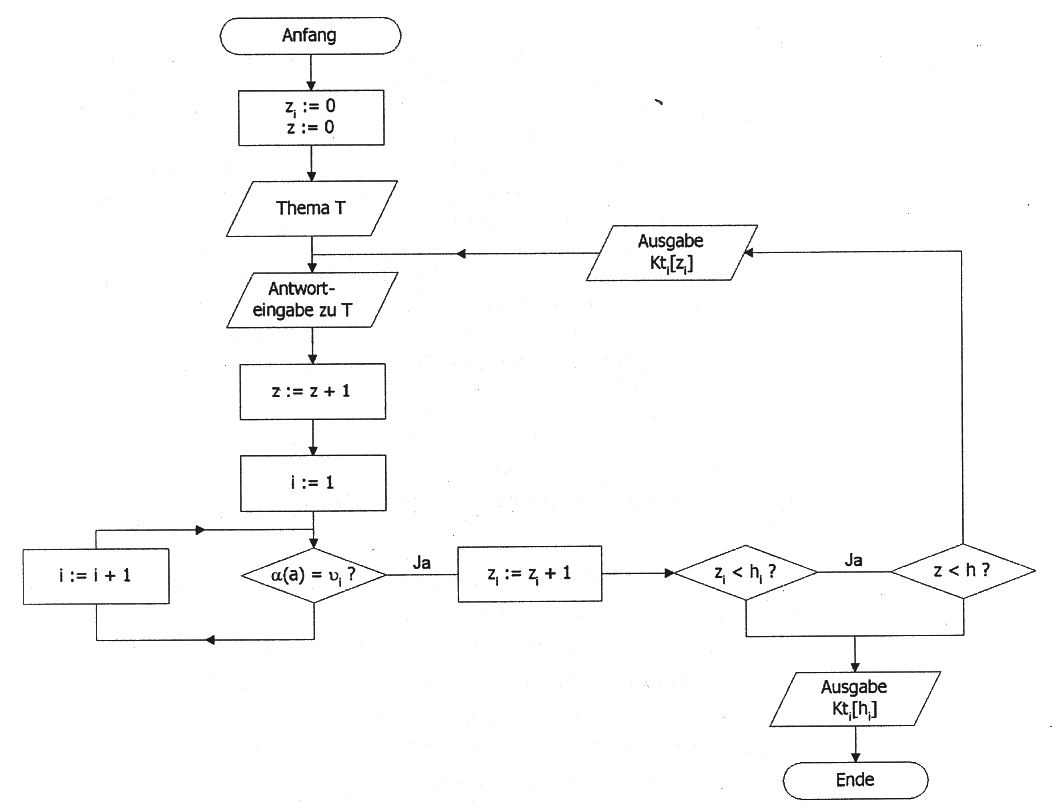
A response analysis a is an effective procedure, where every possible answer a is related to a special answer value vi.

The response analysis can be taken as a function a : A -> V. For every answer a a special answer value vi = a(a) is calculated.

An answer value consists of two things: an answer key (realized by a function with boolean values) and a list Kt[] of commentaries (which are shown separately, if this answer value is used).

An answer key is practically realized as a function with boolean values, which is descriped with some GeoScript-commands. This function checks if the geometrical figure is to be in a special state. For example, the answer key calculates, if two points are incident or if a controller has a special value.

The structure of the response analysis in Geometria is shown in following diagramm.

 

How to describe a response analysis in GeoScript?

The definition of an answer analysis in a script is divided into a main section and several subsections.

Main section:

In the main section the total maximum number of MAX_ANSWER is specified by possible answer attempts. If the value is set to 0, then the pupil has an unlimited number of attempts. Furthermore a list condition[1..n] is to be indicated by GeoScript-functions in the main section. The main section is enclosed by the two commands <problem> and </problem>.

Example:

<Problem>
MAX_ANSWER = 3
condition[1] = "calculate(r) < 0.26"
condition[2] = "calculate(r) > 0.24"
condition[3] = "calculate(r) < 0.51"
condition[4] = "calculate(r) > 0.49"
</Problem>

Comment:

The leaner has got three trials to solve the problem. The four conditions include GeoScript-functions, which checks, if the variable r has got a special value. The value of every variable condition must be always true (1) or false (0).

Sub sections:

In each subsection an answer value vi and an associated list Kt[] with answer comments are defined. To the description of an answer value belongs the indication of the answer key, which is specified by a boolean connection of the GeoScript functions (condition[1..n]) defined in the main section. The answer comments are described in a list commment[1..h]. Every answer comment must be written only in one line. To force a line break one can use the command"/n".

Each subsection for the definition of an answer value is enclosed by the two commands <Answer i> and </Answer i>.

Example:

<Answer 1>
key = "condition[1] AND condition[2]"
comment[1] = "Right. /n This is the solution."
</Answer 1>

<Answer 2>
key = "condition[3] AND condition[4]"
comment[1] = "Your answer is not right. Just try again."
comment[2] = "Your answer is not right. The solution is ..."
</Answer 2>

<Answer 3>
key = "1"
comment[1] = "Your answer is not right. Just try again."
comment[2] = "Your answer is not right. The solution is ..."
</Answer 3>

Notes:

  • The variable MAX_ANSWER defines the absolut number of trials. If MAX_ANSWER = 0, than there is no limit of trials.
    (Example: Image vector)

  • For every answer value there can be defined an arbitrary number of commentaries
    (Image vector - Example with two or three commentaries per answer value).

  • The order of the answer keys in the defined sub sections is important. Geometria proves first the first answer key, than the second, and so on. To be sure, that for every possible answer there is an answer value, the last answer key should have the value "1" (true).

  • If the absolut number of trials MAX_ANSWER is reached and the leaner has not succeded in solving the problem, the boolean system variable showProblemSolution becomes true. One can use this in combination with the hide-command to present a solution fiugre to the leaner. (Example: Image vector)

Excersises

Exercise 1

a) Change the response analysis in figure Algebra of Sets,
that (S1) becomes to ((A + B) Ç C) \ A = {P}.

b) Choose an equation on your own and construct an according figure
with response analysis.

 

Exercise 2

Choose one of the discrete math examples and develop a similar
but new exercise with response analysis.

 

Exercise 3

a) Change the response analysis in figure Image vector that f(x, y): = (–y, x).

b) Choose a function f(x, y) equation on your own and construct an according figure
with response analysis.