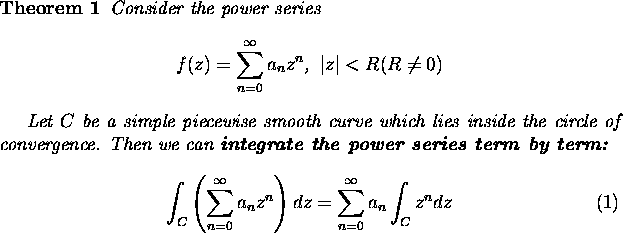
.The function f(z) defined by the power series is continuous on C, so the
integrals in (1) are well-defined. We need to show that
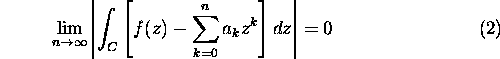
Since C lies inside the circle of convergence, the series converges
uniformly on C to f(z). For any 
, there is an 
so
that, for all z on C,
By the triangle inequality for integrals and the above inequalities,
for 
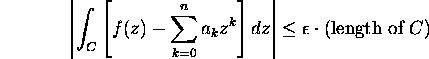
Since is arbitrary, the limit in (2) is zero.
