Some experiments on using interactive problem sets built around mathematical Java applet constructions

Contents

1. How this work in Joensuu began?

Since 1997, we have had several consecutive projects aiming to increase the role of computer-assisted-learning (CAL). For example,

• Matlab-based visualizations for Differential Equations have been used for many years,
• Abstract Algebra was taught several times using ISETL-programming and working in small cooperative groups,
• use of Maple symbolical-gaphical computer program has become a standard supplement in central courses, and
• special courses on the use of technology have been established

After 1999, interactive JavaSketchpad animations have been more or less widely used in Analysis and especially Linear Algebra.

Javasketchpad was introduced to us by Sebastian Lisken from Bielefeld, in a couple of seminars held by him and some cooperators.

Since 2001 we have conducted a four-year pilot project under the umbrella of a larger project called Virtual University of Eastern Finland (Joensuu, Kuopio and Lappeenranta). In the future a few cooperatively arranged courses will be practically “virtual”, e.g. with video lectures and computerized exercises. These developmental efforts, leading to new ways of teaching and new kinds of learning processes, have also invoked the need of follow-up and research activities.

Here we shall introduce a way to use interactive dynamical pictures combined with appropriate problem sets in learning basic mathematical concepts like function, binary operation and eigenvalue, and we shall also take a look at most recent development and research work being done by IPN and Joensuu.
 

2. What are "interactive dynamical sketches"?

Example 1.
The following picture is a part of a series of sketches intending to show the graphical meaning of Gaussian elimination in solving systems of linear equations of type (see 2DLines.htm)

ì í î ax + by = c dx + ey = f

This page requires a Java capable browser.
The interativity means possibility to drag point or to push control buttons. Complicated geometrical or algebraic constructions can be built depending on those dragable (free or somehow restriced) points.

The history of dynamical sketches dates back to the -70-80's and France, where the state-of-the-art computer program Cabri Géomètre was developed. Today there are several competing programs like Geometer's Sketchpad, Cinderella, Euklid. Initially these programs were used locally on stand-alone computers, and the essential idea included creating object. This feature is more difficult with Java and browser conducted sketches but, on the other hand, we can have more precise control over the students activities. This is important in creating distant learning materials. In Geometria applet construction one can also ask for evaluating the present state of the picture, and receive the comments or advice that the creator has programmed in it. This special feature in Geometria, built by Dr. Ehmke, is called response analysis.

Example 3. A Geometria sketch on sets.

Drag the points P, Q and R to such places in the Venn-diagram that

1) P belongs to A \ B

2) Q belongs to B \ A

3) R belongs to

(A \ B) È (B \ A)

The black rectangle represents the base set.
The red points you may move by mouse. When finished, press the Evaluate-button "Evaluate".

 
 

Original Aims of the Work  With these kind of pictures (or "comics") combined with properly selected problems requiring students own activity, and perhaps some calculations, too, we expect that the students will acquire deeper connections with the procedural and conceptual understanding also the weaker students would be able to build viable mental models of (initial and composed) mathematical objects, becoming hopefully able to imagine "mental animations" students become more motivated and thoughtful in their studies some degree of "transfer" would take place, i.e. students will adopt these ideas into their own professional profile

3. Reseach components

A. General observations

• Binary Operations and Scaling Functions (identification and puzzles)
• Linear Independence and Basis in Linear Space
• linear transforms in the Euclidean plane (Part I and Part II)

• what the students think of using computers as learning equipment
• whether this new kind of activities and exercises were accepted and appreciated by the students
• how well the students manage on their own
• how reliable the techniques would appear

Our general observations include:

• students get quickly engaged with the worksheet problems, so that
• it is difficult (and hopefully unnecessary) to gain their attention for more information, therefore
• the worksheets should be optimally self-explaining (enough but not too much info)
• there are still students that are not familiar with computers
• some simply have negative attitude for computers or CAL

The students had had traditional paper-and-pencil exercises and two Maple sessions about matrix algebra before the dynamical picture activities. Before and after the Binary Operation and Scaling demonstrations the students (about 60) were asked about their opinions to some statements, the scale being
disagree - almost disagree - nearly agree - agree
 

No	Statement, for which students agreed or nearly agreed before the activities	%
1	I believe that computers support well the teaching and learning of mathematics.	98,2
2	I believe that computers support well the teaching and learning of linear algebra.	93,0
3	I feel that, in general, working with computers is viable (suits well) for studying mathematics.	86,0
4	I feel that, in general, working with computers increases motivation in studying mathematics.	78,9
5	I feel that, in general, working with computers is advantageous for my learning results in studying mathematics.	63,2

The opinions were almost the same, some increase (14 %-units) was found in statement 5. A more precise picture of the changes in opinion can be seen in the following Table.
 

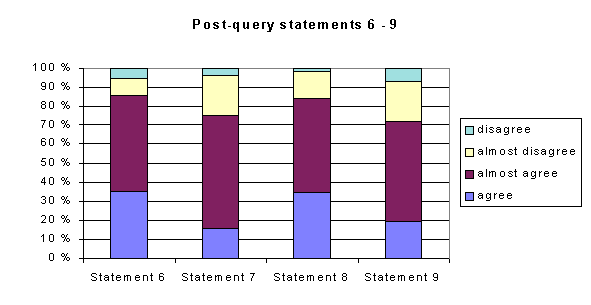
Furthermore, some more specific statements about the activities were posed:
 

6.	Animations clarified the topic to be learned.
7.	Verbal questions helped me in understanding the topic to be learned.
8.	Animation based exercises done alone with the computer suited well with the topic to be learned.
9.	I believe that I learned this topic better with the computer than with traditional teaching.

and the results are shown below:

About students' success

1) definition identification problems
2) verbal-symbolic-graphic (VSG) identification problems
3) production problems (G to V and G to S).
 

Part I: VSG-identification problems (GV, GS) Binary Operation

The poorest results were seen when the domain is not the whole of what is seen. One problem here is that since the students have from school some practical knowledge of functions (graph, formula), they are not open to change of the new point of view, the role of definition. Especially the strict roles of domain and co-domain is easily ignored. Another reason for poor performance in the definition identifying problems can be found

a) in the way the figure represents the operation (how to arrange partial domains, co-domains)
b) the way the student uses it (e.g. does not drag everything)
 

Part II: VSG-identification problems (GV, GS) Binary Operation

Example 5. There were 8 correct combinations (two animations could be combined to two expressions both)
 

All 8 correct pairs	13
7 correct pairs, no false pairs	4
6 correct pairs, no false pairs	7
5 correct pairs, no false pairs	2
1 false pair, others correct	5
correct pairs at least as many as false ones	24
more false pairs than correct	9

Part III: VSG-production problems GV, GS Binary Operation

Example 6. This is how the students managed:
 

Puzzle	Correct	Not correct, but something OK	No idea	No answer	Symbolical form
1	48	11	4	1
2	49	10	3	2
3	27	15	18	4
4	15	37	10	2

About results of other worksheets

Function Demo discussions can be found at
http://www.joensuu.fi/mathematics/MathDistEdu/Crete2002/index.html

Many of the Javasketchpad worksheets were preliminarily tested in the University of Caen in November 2002, and more thorough testing is planned to take place in November 2003.
 

B. Project "From Visual Animations to Mental Models ..."

See also Lehtola's Presentation

http://www.joensuu.fi/mathematics/DidMat/Ehmke/JOENSUU2002/discrete/DMMateriaalinTestausJaTuloksia.html

A new ongoing study concerning the use of dynamical sketches is supported 2003-2004 by the Academy of Finland and DAAD in Germany. The research problem is about how the students really act when struggling with the interactive problems.
The goal is to produce a classification system for the different ways students play with the worksheets. This is supposed to help in the design of more functional material.

The research was started in Autumn 2002 by an experiment in Joensuu. The experimental worksheets can be reached from
http://www.joensuu.fi/matematiikka/kurssit/JohdantokurssiTKD.html
http://www.joensuu.fi/matematiikka/kurssit/JohdKFDRatk.html
 

The pre-test and post-tests were arranged within three two-hour sessions, each participated by some 20 students. Some students made this alone, even though they were encouraged to work in pairs. The test groups were Autumn 2002 first year students on an introductory course for mathematics majors. In the pre-test part there were 17 sketches concerning sets, relations and functions.

Since the students had no experience with this kind of activities, the test was started by 4 examples examined together with the teachers, one about sets (#1), one about relations (#1) and two about function (#5 and #7).

The pre-test problems, which the students had to treat themselves, were structured as a series of short www-pages. The students were asked to start and adjust the Camtasia-captured recording area before answering the first problem.
The problems were

Set Theory #2 and #3
Relations #2 and #3
Functions #1–4, #6, #8–15

First observations
The reseach material consists of screen-captured video files recorded from students’ work.
About 40 recording we captured and Lehtola examined 20 of them briefly in November 2002.

The students managed well with the exercises.
The results concerning functions were very good, at least when compared to the Function Demo referred above.
Hints and links to definitions were used rarely. In function problems a greater deal of students used dragging the variable x than using the animate-facility. One student did not use either at all. In problems where it was possible to follow the function’s behaviour also in the xy-coordinate system, about one third did not use this. There would seems to be need for better advice (?).
Of course there seemed to be students that did very well with minimum of advice.

The applet techniques was found problematic, several students had difficulties in the applet invoking. There were horizontal and vertical lines missing, at least in the recordings.

Second level
The research material is being analysed more deeply by Ehmke&Co in the Leibniz Institute in Kiel and Joensuu.
Now the video-recordings and students' answers have been coded to SPSS, and the combining work is about to start.
 

Back to Math Dist Edu (local)